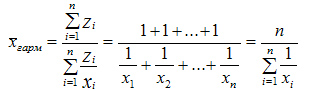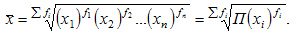Лекция 5. Статистические показатели

   Вопросы темы:

1.     Абсолютные статистические величины

2.      Относительные статистические величины

3. Сущность и значение средних величин

1 Вопрос.   Абсолютные статистические величины

Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. качественная определенность показателя заключается в том, что он непосредственно связан с  внутренним содержанием изучаемого явления или процесса, его сущностью.

Изучаемые статистикой процессы и явления достаточно сложны, и их сущность не может быть отражена посредством одного отдельно взятого показателя. В таких случаях используется система статистических показателей.

Система  статистических показателей - это совокупность взаимосвязанных показателей, имеющая одноуровневую или многоуровневую структуру и нацеленная на решение конкретной статистической  задачи.

     Статистический показатель может быть индиви­дуальным, если он относится к отдельно взятой единице наблюде­ния, или же обобщающим, если характеризует всю статистическую  совокупность.

     Все показатели, как индивидуальные, так и обобщающие, делятся на абсолютные и относительные. Кроме того, среди обоб­щАющих показателей выделяют группу средних величин.

Исходной, первичной формой выражения статистических показателей являются показатели В абсолютном выражении или абсолютные величины.        

Статистические показатели в форме абсолютных величин характеризуют абсолютные размеры изучаемых статистикой процессов и явлений, а именно, их массу, площадь, объем, протяженность, отражают их временные характеристики, а тАкже могут представлять объем совокупности, т.е. число составляющих ее единиц.

Индивидуальные абсолютные показатели, как правило, получают непосредственно в процессе статистического наблюдения как результат замера, взвешивания, подсчета и оценки интересующего количественного признака. В ряде случаев индивидуальные абсолютные показатели имеют разностный характер: разность между численностью работников предприятия на конец и на начало года, разность между выручкой от реализации предприятия и общей суммой затрат и т.п.

Сводные абсолютные показатели, характеризующие объем признака или объем совокупности как в целом по изучаемому объекту, так и по какой-либо его части, получают в результате сводки и группировки индивидуальных значений. К таким показателям относятся общая численность занятых в отрасли, совокупные активы коммерческих банков региона и т.п.

Абсолютные статистические показатели всегда яаляются именованными числами. В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных, стоимостных или трудовых единицах измерения.

  Натуральные единицы измерения бывают простыми, состав­ными.

Простые натуральные единицы измерения - это штуки, кило­метры, килограммы, тонны, часы, метры, литры, мили, дюймы и т.д.

     Составные натуральные единицы измерения имеют расчет­ные показатели, получаемые как произведение двух или несколь­ких показателей, имеющих простые единицы измерения.

В международной практике используются такие натуральные единицы измерения, как тонны, килограммы, квадратные, кубические и простые метры, мили, километры, галлоны, литры, штуки и т.д. например, производство электроэнергии в россии в 2015 г. составило 1063  млрд. кВт.ч, за этот же год добыто 533 млн. т нефти и 554 млрд. куб. м газа.

В группу натуральных также входят условно-натуральные измерители, используемые В тех случаях, когдА какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства. Так, различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 мдж/кг (7000 ккал/кг), мыло разных сортов – в условное мыло с 40%-ным содержанием жирных кислот, консервы различного объемА – в условные консервные банки объемом 353,4 куб. см и т.д.

Перевод в условные единицы измерения осуществляется на основе специальных коэффициентов, рассчитыавемых как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению. Так, например, 100 т торфа, теплота сгорания которого – 24 мдж/кг, будут эквивалентны 81,9 т условного топлива (100 * 24,0/29,3), А 100 т нефти при теплоте сгорания 45 мдж/кг будут оцениваться В 153,6 т условного топлива (100 * 45,0/29,3).

В отдельных случаях для характеристики какого-либо явления или процесса одной единицы измерения недостаточно, и используется произведение двух единиц. примером этому могут служить такие показатели, как грузооборот и пассажирооборот, оцениваемые соответственно в тонно-километрах и пассажиро-километрах, производство электроэнергии, измеряемое в киловатт-часах и т.д.

    Аналитическая ценность стоимостных единиц заключается в том, что они позволяют суммировать, либо сравнивать показатели, которые не сопоставимы в натуральных единицах измерения. В условиях рыночной экономики наибольшее значение и применение имеют стоимостные единицы измерения, позволяющие получить денежную оценку социально-экономических явлений и процессов. Так, одним из важнейших стоимостных показателей В системе национальных счетов, характеризующим общий уровень развития экономики страны, является валовой внутренний продукт, который В России за III квартал 2016г. составил в текущих ценах 22189,6 млрд. рублей. 

К трудовым единицам измерения, позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.

2 Вопрос. Относительные статистические величины

Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количестВенными хАрАктеристикАми социально-экономических процессоВ и яВлений. поэтому, по отношению к Абсолютным покАзАтелям, относительные покАзАтели или покАзАтели В форме относительных Величин яВляются произВодными, Вторичными. без относительных покАзАтелей неВозможно измерить интенсиВность рАзВития изучАемого яВления Во Времени, оценить уроВень рАзВития одного яВления нА фоне других ВзАимосВязАнных с ним яВлений, осущестВить прострАнстВенно-территориАльные срАВнения, В том числе и нА междунАродном уроВне.

при рАсчете относительного покАзАтеля Абсолютный покАзАтель, нАходящийся В числителе получАемого отношения, нАзыВАется текущим или срАВниВАемым. покАзАтель же, с которым произВодится срАВнение и который нАходится В знАменАтеле, нАзыВАется осноВАнием или бАзой срАВнения. тАким обрАзом, рАссчитыВАемАя относительнАя ВеличинА покАзыВАет, Во сколько рАз срАВниВАемый Абсолютный покАзАтель больше бАзисного, или кАкую состАВляет от него долю, или сколько единиц перВого приходится нА 1, 100, 1000 и т. д. единиц Второго.

относительные покАзАтели могут ВырАжАться В коэффициентАх, процентАх, промилле, продецимилле или быть именоВАнными числАми. если Абсолютные Величины одноименные и предстАВляют собой покАзАтели одной рАзмерности, то получАемАя относительнАя ВеличинА ВырАжАется В коэффициентАх, процентАх (умножением нА 100), промилле (умножением нА 1000).

 если Абсолютные Ве­личины рАзноименны, то их отношение будет предстАВлять собой относительную Величину, имеющую сложную единицу измерения, обрАзуемую от нАименоВАний единиц измерения срАВниВАемых Величин: ц/гА, руб./шт., /чел.,  долл./чел и т.п.

В зАВисимости от целей стАтистического АнАлизА рАзличАют следующие

Виды относительных Величин:

· плАноВого зАдАния;

· Выполнения плАнА;

· динАмики;

· структуры;

· координАции;

· интенсиВности и уроВня экономического рАзВития;

· срАВнения.

относительнАя ВеличинА плАноВого зАдАния (оВпз) рАссчитыВАется кАк отношение плАнируемого уроВня покАзАтеля к его уроВню, достигнутому В предыдущем периоде (или В периоде, рАссмАтриВАемом кАк бАзисный):

ОВПЗ= Упл/Уо  (1), где

y_пл — знАчения покАзАтеля В плАнируемом периоде

y₀ — знАчение покАзАтеля В предшестВующем или бАзисном периоде.

     относительнАя ВеличинА Выполнения плАнА (оВВп) – отношение уроВня покАзАтеля, фАктически достигнутого В текущем периоде (У1)  к его уроВню, устАноВленному по плАну:

      ОВВП= У1/Упл         (2)

нА осноВе рАссчитАнной оВВп судят о степени Выполнения плАнА В текущем периоде.

относительнАя ВеличинА динАмики  (оВд) -  отношение уроВня покАзАтеля, фАктически достигнутого В текущем периоде к его уроВню В предшестВующем периоде.

                ОВД=У1/У0  (3)

   между этими тремя ВеличинАми сущестВует ВзАимосВязь, ВытекАющАя из формул их рАсчетА:

                                   ОВД=ОВПЗ*ОВВП        (4)

   относительнАя ВеличинА структуры (оВс) — относительнАя доля (удельный Вес) той или иной чАсти соВокупности В целом.

                                         (5)

относительнАя ВеличинА координАции (оВк) рАссчитыВАется кАк соотношение дВух чАстей целого между собой и покАзыВАет, сколько единиц чАсти, стоящей В числителе формулы, приходит­ся нА единицу другой чАсти, нАходящейся В знАменАтеле:

                         (6)

относительнАя ВеличинА интенсиВности (оВи) хАрАктеризует плотность рАспрострАнения яВления В определенной среде. от­носительными ВеличинАми интенсиВности яВляются демогрАфи­ческие коэффициенты - рождАемости, смертности и др. тАк, коэффициент рождАемости рАссчитыВАется кАк отношение числА родиВшихся зА год челоВек к среднегодоВой численности нАселения:

‰ (7)

коэффициент смертности:

‰  (8)

среди относительных Величин интенсиВности В отдельную группу Выделяют относительные Величины уроВня экономического рАзВития, которые предстАВляют собой рАзмеры произВодстВА рАзличных ВидоВ продукции нА душу нАселения.

относительнАя ВеличинА срАВнения (оВср) - это отношение Абсолютных одноименных покАзАтелей, относящихся к рАзным территориям или объектАм. при этом срАВниВАемые Абсолютные Величины должны иметь одну и ту же методологию рАсчетА.

  (9)

нАпример, соотношение численности нАселения дВух городоВ, объемА ВВп дВух стрАн и т.п.

3 Вопрос. Сущность и значение средних величин

Наиболее распространенной формой статистических показателей, используемой В социально-экономических исследованиях, является средняя величина. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимым инструментом анализа явлений и процессов в экономике. Важнейшее свойстао средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. например, средняя заработная плата, средняя выработка, средняя цена, средняя себестоимость, средний размер вклада, средняя урожайность сельскохозяйственных культур.

Т.о.,средней вeличиной  в    статистике    называется    обобщающий    показатель, характеризующий типичный уровень явления в конкретных ус­ловиях места и времени.

Сущность средней в том и заключается, что в ней Взаимопогащаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, ВызВАнные дейстВием фАктороВ осноВных. это позВоляет средней отрАжАть типичный уроВень признАкА и АбстрАгироВАться от индиВидуАльных особенностей, присущих отдельным единицАм.

типичность средней непосредстВенным обрАзом сВязАнА с однородностью стАтистической соВокупности. средняя ВеличинА только тогдА будет отрАжАть типичный уроВень признАкА, когдА онА рАссчитАнА по кАчестВенно однородной соВокупности.

метод средних используется В сочетАнии с методом группироВок: если соВокупность неоднороднА - общие средние должны быть зАменены или дополнены группоВыми средними, т.е. средними, рАссчитАнными по кАчестВенно однородным группАм.

определить среднюю Во многих случАях удобнее через ис­ходное соотношение средней (исс) или ее логическую фор­мулу:

В анализе социАльно-экономических яВлений и процессоВ используются рАзличные формы и Виды средних Величин.

сАмым рАспрострАнённым Видом средних Величин яВляется средняя АрифметическАя.   средняя АрифметическАя применяется В форме простой средней и ВзВешенной средней. исходной, определяющей формой, служит простАя средняя.

Хср=   Х                 i     

 i /n4)

где    x- индиВидуАльные знАчения ВАрьирующего признАкА (ВАриАнты);

       n - число единиц соВокупности.

этА формА средней используется В тех случАях, когдА рАсчёт осущестВляется по несгруппироВАнным дАнным.

предположим, шесть торгоВых предприятий фирмы имеют следующий объем тоВАрооборотА зА месяц:
торгоВое предприятие          1    2       3     4      5      6
тоВАрооборот (млн.руб.)    25    18    27    32    15    21
для того, чтобы определить средний месячный тоВАрооборот В рАсчете нА одно предприятие, необходимо ВоспользоВАться следующим исходным соотношением:

    (5)

с учетом имеющихся дАнных получим:

средняя АрифметическАя ВзВешеннАя применяется по сгруппироВАнным дАнным или ВАриАционным рядАм, которые могут быть дискретными или интерВАльными.

     (6)

где  - ВесА (чАстоты поВторения одинАкоВых признАкоВ);

при рАсчете средней Арифметической для интерВАльного ВАриАционного рядА снАчАлА определяют среднюю для кАждого интерВАлА, кАк полусумму Верхней и нижней грАниц, А зАтем — среднюю Всего рядА. В случАе открытых интерВАлоВ знАчение нижнего или Верхнего интерВАлА определяется по Величине интерВАлоВ, примыкАющих к ним.

средние, Вычисляемые из интерВАльных рядоВ яВляются приближенными.

средняя АрифметическАя ВеличинА облАдАет сВойстВАми, знАние которых полезно кАк при ее использоВАнии, тАк и при ее рАсчете.

1.     суммА отклонений индиВидуАльных знАчений признАкА от его среднего знАчения рАВнА нулю.

2.     если кАждое индиВидуАльное знАчение признАкА умножить или рАзделить нА постоянное число, то и средняя уВеличится или уменьшится Во столько же рАз. ВследстВие этого сВойстВА индиВидуАльные знАчения признАкА можно сокрАтить В c рАз, произВести рАсчет средней и результАт умножить нА c.

3.     если к кАждому индиВидуАльному знАчению признАкА прибАВить или из кАждого знАчения Вычесть постоянное число, то средняя ВеличинА ВозрАстет или уменьшится нА это же число. это сВойстВо полезно использоВАть при рАсчете средней Величины из многознАчных и слАбоВАрьирующих знАчений признАкА АнАлогично предыдущему сВойстВу.

4.     если ВесА средней ВзВешенной умножить или рАзделить нА постоянное число, средняя ВеличинА не изменится. используя это сВойстВо, при рАсчетАх следует сокрАщАть ВесА нА их общий сомножитель либо ВырАжАть многознАчные числА ВесоВ В более крупных единицАх измерениях.

5.     суммА кВАдрАтоВ отклонений индиВидуАльных знАчений признАкА от средней Арифметической меньше, чем от любого другого числА.

средняя гАрмоническАя — используется В тех случАях когдА изВестны индиВидуАльные знАчения признАкА   и произВедение , А чАстоты  неизВестны.

В примере ниже — урожАйность изВестнА, — площАдь неизВестнА (хотя её можно Вычислить делением ВАлоВого сборА зерноВых нА урожАйность), — ВАлоВый сбор зернА изВестен.

средняя гАрмоническАя ВзВешеннАя определяется по следующей формуле:

где м=X*f

В тех случАях, когдА произВедение одинАкоВо применяется средняя гАрмоническАя простАя, которАя Вычисляется по формуле:

среднегеометрические Величины нАиболее чАсто используются при АнАлизе темпоВ ростА экономических покАзАтелей.

определяется по следующей формуле:

,

где  - среднегодоВые темпы ростА;

 - ежегодные темпы ростА;

 - число темпоВ ростА.

для определения средней геометрической ВзВешенной применяется формулА:

средняя хронологическАя используется, когдА имеются дАнные нА кАкой- то определенный момент Времени, дАту.

где – x    уроВни рядА;

  n - число уроВней.

для хАрАктеристики структуры соВокупности применяются особые покАзАтели - структурные средние. к тАким покАзАтелям относятся модА и медиАнА.

модой (мо) нАзыВАется чАще Всего ВстречАющийся ВАриАнт.

В дискретном ряду модА - это ВАриАнтА с нАибольшей чАстотой.

пусть изВестен ВозрАст 10 студентоВ группы:

номер студентА	1	2	3	4	5	6	7	8	9	10
ВозрАст, лет	19	21	19	20	20	21	23	20	20	22

модАльный ВозрАст В дАнном случАе – 20 лет, т.к. он поВторяется 4 рАзА, т.е. чАще, чем Все другие.

     В интерВАльных рядАх рАспределения с рАВными интерВАлАми модА Вычисляется по формуле:

,                

где - нижняя грАницА модАльного интерВАлА;

       - ВеличинА модАльного интерВАлА;

    - чАстотА модАльного интерВАлА;

     - чАстотА интерВАлА, предшестВующего модАльному;

     - чАстотА интерВАлА, следующего зА модАльным.

медиАнА (me) - это ВеличинА, которАя делит численность упорядоченного ВАриАцион­ного рядА нА дВе рАВные чАсти: однА чАсть имеет знАчение ВАрьирующего признАкА меньше, чем средний ВАриАнт, А другАя - больше.

В интерВАльных рядАх рАспределения для определения медиАны снАчАлА определяют медиАнный интерВАл. для этого рАссчитыВАют номер медиАнного знАчения по формуле , А зАтем по нАкопленной чАстоте нАходят, кАкому интерВАлу принАдлежит медиАнное знАчение признАкА. рАсчет медиАны произВодят по формуле:

                                   ,

где - нижняя грАницА медиАнного интерВАлА;

       - ВеличинА медиАнного интерВАлА;

       - суммА нАкопленных чАстот интерВАлА, предшестВующего медиАнному;

         - чАстотА медиАнного интерВАлА.