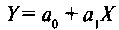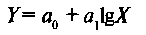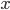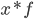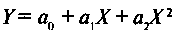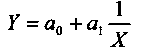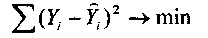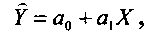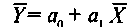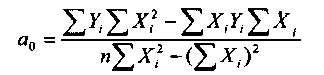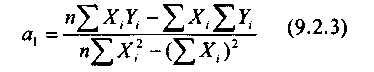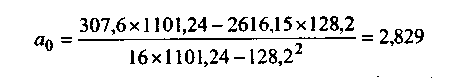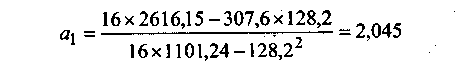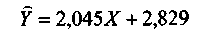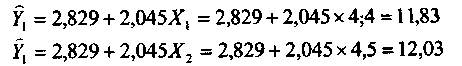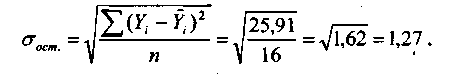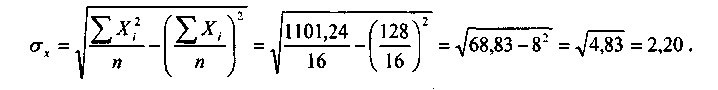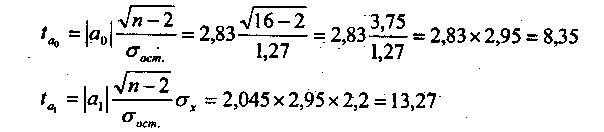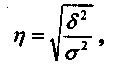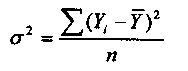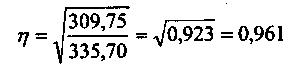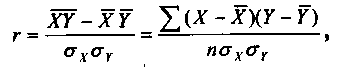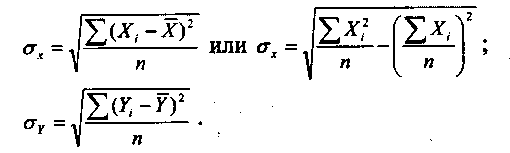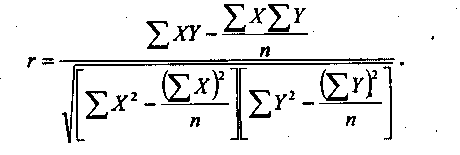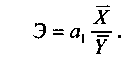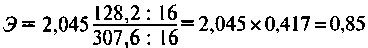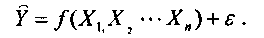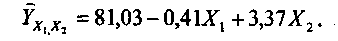Лекция 10. Статистическое изучение взаимосвязей социально – экономических явлений

Вопросы темы:

1. Понятие о статистической и корреляционной связи

Изучение связей между различными явлениями и процессами является одной из важнейших задач статистики. Статистика позволяет определить количественные характеристики связей, выявленных в результате их теоретического сущностного анализа. Применяемые для решения этой задачи специальные приемы и методы разнообразны и выбор их в каждом конкретном случае зависит от характера используемой информации и целей анализа.

Связь между различными явлениями и их признаками может быть функциональной или статистической.

Связь между результативным признаком Y и факторным признаком X называется функциональной, если каждому значению независимой переменной (X) соответствует одно определенное значение зависимой переменной (Y). Такую связь можно представить уравнением:

где Y- результативный признак (i= 1, 2, ...п);

X - факторный признак;

f(X)- функция связи результативного и факторного признаков.

В социально-экономической сфере функциональные связи наблюдаются очень редко.

Статистическая связь - это связь, при которой случайная величина Y реагирует на изменение величины X (случайной или неслучайной) изменением закона распределения.

Такая особенность статистической связи обусловлена тем, что помимо рассматриваемого фактора X на изменение Y влияет ряд неучтенных или неконтролируемых (случайных) факторов. В результате статистическая связь может быть представлена следующим уравнением:

где - расчетное значение результативного признака;

f (X_i ) - часть , сформированная под влиянием фактора X (или нескольких учтенных факторов);

- часть , возникающая под влиянием неучтенных факторов.

Принципиальной особенностью статистической связи является проявление ее не в единичных случаях, а только в их массе. Проявление такой связи базируется на законе больших чисел: только при достаточно большом объеме совокупности индивидуальные особенности каждой ее единицы сгладятся, случайности взаимопогасятся и существенная зависимость проявится.

Частным случаем статистической связи является корреляционная связь. При такой связи среднее значение случайного результативного признака закономерно изменяется под влиянием другой (или других) случайных величин.

Корреляционные связи присущи многим социально-экономическим явлениям. Примером такой связи является зависимость производительности труда рабочего от его квалификации: производительность труда выше у рабочих с более высокой квалификацией. Это утверждение справедливо в целом для достаточно большого числа случаев, но оно не означает, что у двух рабочих одинаковой квалификации производительность труда обязательно будет равной. Вероятнее всего она будет разной. И это объясняется тем, что на производительность труда рабочих кроме квалификации влияют еще и другие, неучтенные в данном случае факторы: возраст и физическое состояние рабочего, уровень организации труда и целый ряд других условий производства.

Поскольку корреляционные связи проявляются только в массе случаев, они изучаются по информации, полученной в процессе статистического наблюдения и отражающей совокупное действие всех причин и условий на изучаемый признак.

Статистические связи могут быть прямые и обратные, прямолинейные и криволинейные, однофакторные и многофакторные.

При прямой связи направление изменения результативного признака совпадает с направлением изменения признака-фактора. Например:

• с ростом количества внесенных на 1 га удобрений растет урожайность;

• сокращение остатков оборотных средств снижает средние издержки предприятия.

В противном случае связь между двумя признаками называется обратной. Например, рост производительности труда способствует сокращению себестоимости продукции.

Прямолинейной называется связь, которая графически может быть представлена прямой линией, а аналитически — уравнением Y= а+ bХ.

Связь, для графического изображения и аналитического выражения которой используются такие функции как парабола, гипербола и т.п., называется криволинейной

Однофакторной (парной) называется связь двух признаков. Например, зависимость между себестоимостью продукции и прибылью предприятия. Связь, учитывающая влияние на результативный признак множества факторов, называется многофакторной или множественной. Например, связь между производительностью труда в отрасли и специализацией производства, фондовооруженностью труда, уровнем механизации и автоматизации и т.д.

При изучении корреляционной связи социально-экономических показателей необходимо решить следующие задачи:

• проверить возможность связи между изучаемыми показателями и описать эту связь аналитически;

• количественно оценить тесноту связи между факторным (факторными) и результативным признаками.

2. Однофакторный линейный корреляционно-регрессионный анализ

Наиболее разработанной в настоящее время является методология парной корреляции, рассматривающая влияние вариации одного факторного признака Х на результативный признак Y. Теория и методика парной корреляции являются основой более сложных приемов и методов изучения статистических связей.

При изучении парной регрессии показателей социально-экономической сферы используются различные функции (уравнения):

линейная

логарифмическая

показательная

степенная

параболическая

гиперболическая и другие.

Выбор функции, которая наиболее точно выражает связь между анализируемыми показателями, является важнейшим этапом корреляционно-регрессионного анализа. При решении этой задачи необходимо использовать теоретические знания об изучаемом процессе и опыт предыдущих аналогичных исследований. Возможности современной вычислительной техники позволяют выбрать «наилучшую» функцию эмпирически — перебором и оценкой функций разного вида.

Определение параметров выбранной функции осуществляется с помощью метода наименьших квадратов, в основу которого положен критерий минимальности суммы квадратов отклонений эмпирических (фактических) данных (Y) от соответствующих им расчетных значений результативного признака (Y):

Чаще всего используется линейное уравнение парной регрессии

где — теоретическое (расчетное) значение результативного признака, полученное по уравнению регрессии; а₀ , а_х — параметры уравнения регрессии.

Коэффициент а₁ (коэффициент регрессии) показывает на сколько единиц в среднем изменится результативный признак при изменении факторного признака на одну единицу его измерения. Знак при коэффициенте регрессии свидетельствует о направлении зависимости Y от X. при а₁ > 0 — зависимость прямая; при а₁ < 0 — зависимость обратная.

Параметр а₀ показывает среднее значение результативного признака Y при Х= 0 в случае, если в исходных данных имеется нулевое значение факторного признака. Во всех остальных случаях а₀ экономически не интерпретируется и количественно представляет собой «доводку», обеспечивающую равенство:

Параметры уравнения в соответствии с методом наименьших квадратов определяются по формулам:

Определив значение а₀, а₁ и подставив их в уравнение, находим значение , зависящее только от заданного уровня X.

Пример. Построим уравнение парной регрессии, отражающее зависимость годовой заработной платы и выработки продукции рабочих завода.

В этом случае результативным признаком является заработная плата рабочих, а в качестве факторного признака выступает выработка продукции в натуральном выражении.

В табл. 10.1 факторный признак Х проранжирован, и сопоставление параллельных рядов (столбцы 2 и 3) позволяет утверждать, что между рассматриваемыми показателями существует прямая зависимость: с ростом объема выработки увеличивается величина заработной платы.

Таблица 10.1

Распределение рабочих завода по выработке и заработной плате

Исходные данные			Расчет
Номер рабочего	Выработка продукции, тыс. шт.	Заработная плата, тыс. руб.
Номер рабочего
1	2	3	4	5	6	7
1	4,4	9,6	19,36	92,16	42,24	11,83
2	4,5	9,8	20,25	96,04	44,2	12,03
3	6,1	17,5	37,21	306,25	106,75	15,30
4	6,5	17,8	42,25	316,84	115,7	16,12
5	7,0	17,5	49,0	306,25	122,5	17,14
6	7,0	18,8	49,0	353,44	131,6	17,14
7	7,5	17,8	56,25	316,84	133,5	18,17
8	8,0	19,2	64,0	368,64	153,6	19,19
9	8,1	21,0	65,61	441,0	170,1	19,39
10	8,4	19,6	70,56	384,16	164,64	20,01
11	8,5	20,1	72,25	404,01	170,85	20,21
12	9,0	20,6	81,0	424,36	185,4	21,23
13	9,3	22,0	86,49	484,0	204,6	21,85
14	9,5	22,5	90,25	506,25	213,75	22,26
15	12,0	26,0	144,0	676,0	312,0	27,37
16	12,4	27,8	153,76	772,84	344,72	28,19
Итого	128,2	307,6	1101,24	6249,08	2616,15	307,43
Итого

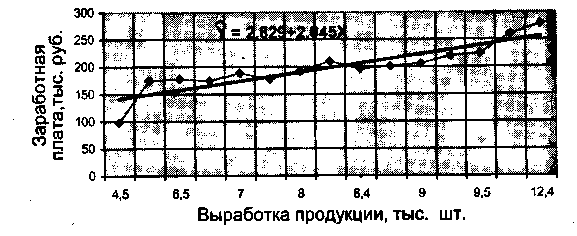
Наличие такой связи подтверждается расположением точек и ломаной линии на корреляционном поле 10.1

Для количественной оценки связи между анализируемыми показателями определим параметры линейного уравнения регрессии:

где - теоретические (расчетные) значения результативного признака (заработной платы), полученные по уравнению регрессии;

а₀, а₁ - параметры уравнения регрессии;

X - выработка продукции.

Используя информацию табл. 10.1, по формулам определения параметров уравнения считаем значения параметров парной регрессии:

Рис. 10.1 Зависимость заработной платы рабочих от выработки продукции

Таким образом, регрессионная модель зависимости заработной платы рабочих от выработки продукции выглядит следующим образом:

Графическое изображение этой функции показано на рис. 10.1 сплошной прямой линией.

Такая зависимость означает, что с ростом выработки продукции в данной совокупности рабочих на 1 тыс. штук, в среднем величина их заработной платы увеличивается на 2,045 тыс. рублей.

Величины, представленные в столбце 7 табл. 10.1 рассчитываются следующим образом:

и т.д.

Правильность расчета параметров уравнения регрессии подтверждает равенство:

(некоторое расхождение объясняется округлением расчетов).

3. Проверка адекватности регрессионной модели

Использование регрессионных моделей для решения практических задач возможно лишь в случае, если они отражают существенные связи. Поэтому так важна проверка адекватности таких моделей, цель которой выяснить, не являются ли параметры полученного уравнения регрессии результатом действия случайных причин.

Значимость параметров парной линейной регрессии применительно к совокупностям объемом не больше 30 проверяют с помощью t-критерия Стьюдента. Для достаточно больших совокупностей используют таблицу интеграла вероятностей нормального закона распределения¹.

Фактические (расчетные) значения t -критерия для а₀ и а₁ определяются по следующим формулам:

где п — объем совокупности;

- среднее квадратическое отклонение фактических значений результативного признака от его расчетных значений;

или - среднее квадратическое отклонение фактических значений факторного признака от его среднего уровня.

Рассчитанные по формулам значения t сравниваются с критическим значением t, определяемым по таблице Стьюдента с учетом уровня значимости и числом степеней свободы . В социально-экономических исследованиях обычно пронимают равным 0,05. Параметр признается значимым, если В этом случае отклоняется гипотеза о том, что значения а₀ и а₁ обусловлены только случайными причинами и связь между Y и Х не носит закономерного характера.

Пример (продолжение). Проверим значимость параметров указанного уравнения.

Таблица 10.2

Расчетные величины, используемые при оценке адекватности регрессионной модели

Номер рабочего

1

2

3

4

5

6

7

1

-2,23

4,97

-9,63

92,74

-7,4

54,76

2

-2,23

4,97

-9,43

88,92

-7,2

51,84

3

2,20

4,84

-1,73

2,99

-3,93

15,44

4

1,68

2,82

-1,43

2,04

-3,11

9,67

5

0,36

0,13

-1,73

2,99

-2,09

4,37

6

1,66

2,76

-0,43

0,18

-2,09

4,37

7

-0,37

0,14

-1,43

2,04

-1,06

1,12

8

0,01

0,00

-0,03

0,00

-0,04

0

9

1,61

2,59

1,77

3,13

0,16

0,03

10

-0,41

0,17

0,37

0,40

0,78

0,61

11

-0,11

0,01

0,87

0,76

0,98

0,96

12

-0,63

0,40

1,37

1,88

2,00

4,00

13

0,15

0,02

2,77

7,67

2,62

6,86

14

0,24

0,06

3,27

10,69

3,03

9,18

15

-1,37

1,88

6,77

45,83

8,14

66,26

16

-0,39

0,15

8,57

73,44

8,96

80,28

Итого

х

25,91

-

335,7

309,75

Для расчета _ост используем данные табл. 10.2 (графа 3), полученные как разность граф 3 и 7 из табл.10.1:

Расчет выполним по данным табл. 10.1 (графы 2 и 4):

Расчетные значения t-критерия Стьюдента:

Уровню значимости при =14 (16 - 2) соответствует критическое значение t-критерия: t_табл.= 2,145.

Таким образом, расчетные значения и значительно превосходят табличное значение t-критерия. Это означает, что оба параметра уравнения значимы и связь между заработной платой и выработкой рабочих в исследуемой совокупности не случайна.

Проверка адекватности регрессионной модели, как правило, дополняется определением тесноты корреляционной связи между результативным и факторным признаком.

Для решения этой задачи используется теоретическое корреляционное отношение:

где - общая дисперсия результативного признака, отображающая совокупное влияние всех факторов на вариацию результативного признака Y, определяется по формуле

- факторная дисперсия результативного признака, отображающая вариацию результативного признака Y только под воздействием изучаемого фактора X, определяется по формуле

В результате:

Теоретическое корреляционное отношение применяется для измерения тесноты связи между результативным и факторным признаком при линейной и криволинейной корреляционной зависимости. Значение его может находиться в пределах от 0 до 1, т.е. . Чем ближе корреляционное отношение к 1, тем теснее связь между изучаемыми признаками.

Рассчитаем как меру тесноты связи между заработной платой и выработкой рабочих. Для этого воспользуемся данными табл. 10.2, полученными по данным табл. 10.2:

Следовательно, изучаемые нами признаки: заработная плата и выработка рабочих связаны достаточно тесно.

Квадрат теоретического корреляционного отношения называется коэффициентом детерминации. В нашем примере он равен 0,923 и означает, что 92,3% вариации заработной платы рабочих обусловлено колеблемостью выработки продукции в натуральном выражении.

При линейной форме связи помимо теоретического корреляционного отношения для измерения тесноты связи может быть использован линейный коэффициент корреляции, предложенный английским математиком К. Пирсоном:

где п — число наблюдений

При небольшом числе наблюдений (п < 20:30), этот коэффициент удобнее вычислять по следующей формуле:

Линейный коэффициент корреляции может принимать значение в интервале: . Отрицательное значение r указывает на обратную связь, его положительное значение — на прямой характер зависимости. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции к 1 (по абсолютной величине), тем теснее связь между изучаемыми признаками. При r = 1 - связь функциональная.

Используя данные табл. 10.1, рассчитаем линейный коэффициент корреляции по формуле:

Квадрат линейного коэффициента корреляции называется линейным коэффициентом детерминации. Его значение всегда находится в пределах от 0 до 1.

Значения теоретического корреляционного отношения и линейного коэффициента корреляции r совпадают только при наличии прямолинейной связи. Эта закономерность используется для оценки формы связи. Если разность между и не превышает 0,1, то связь между изучаемыми признаками можно считать прямолинейной.

В приведенном примере и это значит, что зависимость заработной платы рабочих от выработки продукции в натуральном выражении носит линейный характер.

Для оценки значимости r, так же как и при оценке значимости коэффициентов регрессии, используется t-критерий Стьюдента. Расчетное значение t при этом определяется по формуле:

где п — объем выборки.

В нашем примере соответственно:

это значительно больше, чем критическое значение t = 2,977 при числе степеней свободы 14 = (16 - 2) и уровне значимости = 0,01. Это свидетельствует о значимости коэффициента корреляции и о существенности связи между заработной платой рабочих и выработкой продукции.

Следовательно, регрессионная модель = 2,045Х + 2,829 адекватна, и ее можно использовать в экономическом анализе.

Для интерпретации можно использовать коэффициент эластичности:

Этот коэффициент показывает среднее изменение результативного признака в процентах при изменении факторного признака на 1%.

В нашем примере:

что означает: при росте выработки продукции на 1%, заработная плата рабочих возрастает на 0,85%.

Если данная совокупность и условия работы типичны, то это уравнение можно использовать для планирования и прогнозирования заработной платы рабочих.

4. Многофакторный корреляционно-регрессионный анализ и интерпретация его результатов

Многофакторный корреляционный и регрессионный анализ позволяет количественно оценить влияние на результативный признак не одного, а нескольких факторов.

Задача состоит в нахождении аналитического выражения, наилучшим образом отражающего установленную на основе сущностного анализа связь некоторого числа факторных признаков с результативным. Что в общем виде записывается так:

Выбор типа апроксимирующей функции производится перебором наиболее часто применяемых в корреляционно-регрессионном анализе уравнений. Реализация такого алгоритма в современных условиях при наличии соответствующих программ для персональных компьютеров осуществляется довольно просто.

После выбора апроксимирующей функции определяют значение ее параметров, используя при этом, так же как в случае парной регрессии, метод наименьших квадратов. Затем проводится проверка адекватности полученной модели и в случае, если выявленные с ее помощью связи существенны, приступают к ее экономической интерпретации.

Анализ параметров уравнения множественной регрессии позволяет оценить степень влияния каждого из факторов на результативный признак.

Например, было получено уравнение множественной регрессии, адекватно отражающее зависимость производительности труда рабочих (Y) - дневная выработка продукции (штук) от внутрисменных простоев (минут) – Х₁ и квалификации рабочих (тарифный разряд) - Х₂:

Коэффициент а₁ = - 0,41 показывает, во-первых, что связь между величиной простоев и производительностью труда является обратной и, во-вторых, что с увеличением продолжительности простоев на 1 минуту следует ожидать сокращения дневной выработки одного рабочего в среднем на 0,41 шт.

Коэффициент а₂ = 3,37 свидетельствует, что рост квалификации рабочих на один разряд может привести к росту производительности труда на 3,37 шт.

На основе множественного уравнения регрессии можно проранжировать факторы по силе их влияния на результативный признак.

Для решения этой задачи используют частные коэффициенты эластичности, которые показывают на сколько процентов в среднем изменяется результативный признак при изменении одного из факторов на 1 % и при фиксированном положении других факторов.

Такие расчеты показали, что наибольшее влияние на производительность труда в данном конкретном случае оказывает фактор Х₂ — повышение квалификации на 1 % приводит к росту производительности труда почти на 15%. В то время как сокращение продолжительности простоев на 1% ведет к росту производительности труда только на 5%.

Такой вывод позволяет утверждать, что основным резервом увеличения дневной выработки рабочих является повышение их квалификации.

Для выявления дополнительных резервов роста эффективности производства следует построить регрессионную модель с большим количеством факторов.

Уравнение множественной регрессии может плодотворно использоваться для планирования и прогнозирования результативных признаков в зависимости от изменения факторных признаков.

Сайт создан по технологии «Конструктор сайтов e-Publish»