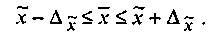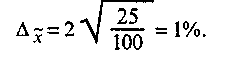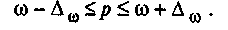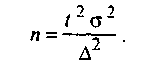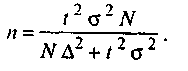Лекция 7. Выборочное наблюдение в экономическом анализе

 

 

Вопросы темы:

1. Понятие о выборочном наблюдении и его значение

2. Основные способы формирования выборочной совокупности

3. Ошибки выборки и определение необходимого объема выборки

 

1 вопрос. Понятие о выборочном наблюдении и его значение

 

Выборочное наблюдение – такое не сплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные определенным образом.

Цель (задача) выборочного наблюдения: по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов статистического наблюдения.

При выборочном наблюдении различают две совокупности:

Генеральная совокупность (N) – совокупность единиц, из которых производится отбор.

Выборочная совокупность (n)– совокупность отобранных для обследования единиц

Причины применения выборочного наблюдения:

1.                 экономия материальных, трудовых затрат и времени;

2.                 возможность более детально и подробно изучит отдельные единицы статистической совокупности и их группы.

3.                 некоторые специфические задачи можно решить только с применением выборочного наблюдения.

4.                 грамотное и хорошо организованное выборочное наблюдение дает высокую точность результатов.

Однако существуют и недостатки выборочного наблюдения

Полученные данные всегда содержат в себе ошибку, так как выборочная совокупность не полностью воспроизводит генеральную совокупность. О результатах наблюдения можно судить лишь с определенной степенью достоверности. Но по сравнению с другими видами наблюдения это достоинство выборочного метода.

В настоящее время выборочное наблюдение находит достаточно широкое применение в обследованиях промышленных и сельскохозяйственных предприятий, изучении цен на потребительском рынке, в обследованиях бюджетов и занятости населения. Выборочный метод является важнейшим источником информации в маркетинговых и социологических исследованиях, в контроле качества продукции; разработаны методологические подходы к применению выборочного наблюдения в аудите.

 

2 вопрос. Основные способы формирования выборочной совокупности

 

При проведении выборочного наблюдения используют следующие способы отбора: собственно - случайный, механический, типический, серийный или их сочетание (комбинированный).

Собственно-случайный отбор заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем проводить такую выборку, нужно убедиться, что все единицы генеральной совокупности имеют равные шансы попасть в выборку, т.е. в полном перечне единиц статистической совокупности отсутствуют пропуски или игнорирования отдельных единиц. Следует, также, четко установить границы генеральной совокупности. Технически сложившейся отбор осуществляется методом жеребьевки или с помощью таблицы случайных чисел.

Механический отбор  применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в распределении единиц. При проведении механической выборки устанавливается пропорция отбора, которая устанавливается соотношением генеральной совокупности и выборочной совокупности.

Типический отбор — отбор, при котором неоднородная генеральная совокупность предварительно разбивается на однородные (типические) группы, из которых случайно производят отбор необходимой численности выборки.

Серийный отбор используется когда единицы наблюдения объединены в небольшие группы (серии), например упаковка с готовой продукцией, студенческие группы. Сущность серийной выборки – серии отбираются собственно случайным, либо механическим способом, а затем осуществляется сплошное обследование внутри отобранной серии.

Комбинированный отбор

Это комбинация рассмотренных выше способов отбора чаще применяется комбинация типичных и серийных серии, т.е. отбор серий из нескольких типических групп.

Различают бесповторный и повторный отбор.

При повторном отборе  каждая единица совокупности может участвовать в выборке несколько раз, т.е. Попавшая в выборку единица после регистрации наблюдаемых признаков возвращаются в генеральную совокупность для участия в дальнейшей процедуре отбора.

Объем генеральной совокупности остается неизменным, что обуславливает постоянное попадание в выборку какой-либо единицы.

На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.

Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.

При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами – изделиями.

Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.

При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен.

Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.

Необходимо отметить, что в выборочную совокупность могут отбираться не только отдельные единицы, но и группы единиц. В первом случае отбор называется индивидуальным, во втором случае - групповым.

Отбор может быть еще многоступенчатым и одноступенчатым, многофразным и однофразным.

Многоступенчатый отбор: из генеральной совокупности сначала извлекаются укрупненные группы, затем более мелкие, и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.

Многофразная выборка: предполагает сохранение одной и той же единицы отбора на всех этапах его проведения. При этом отобранные на каждой последующей стадии единицы отбора подвергаются обследованию, программа которого расширяется (Пример: студенты всего института, затем студенты каких-то факультетов).

 

3 вопрос. Ошибки выборки

В процессе выборочного наблюдения различают следующие виды ошибок:

 

Ошибки регистрации имеют случайный непреднамеренный характер, их можно избежать при правильной организации и проведении выборочного наблюдения.

Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.

Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.

Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.

Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения - оценить репрезентатив­ность (представительность) выборочной совокупности. Различа­ют среднюю и предельную ошибки выборки. Эти два вида оши­бок связаны следующим соотношением:

 

,  (1)

где - предельная ошибка выборки;

- средняя ошибка выборки;

- коэффициент доверия, определяемый в зависимости от уровня вероятности.

Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Так, при случайном повторном отборе средняя ошибка определяется по формуле:

,          (2)

 

при бесповторном:  ,           (3)

где - выборочная (или генеральная) дисперсия;

- объем выборочной совокупности;

- объем генеральной совокупности.

Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

 

,

где  и - генеральная и выборочная средние соответственно;

- предельная ошибка выборочной средней.

 Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки.

 

Пример 1.

Для определения зольности угля в месторождении в порядке случайной выборки было обследовано 100 проб угля. В ре­зультате обследования установлено, что средняя зольность угля в выборке 16%, среднее квадратическое отклонение 5%. В десяти про­бах зольность угля составила более 20%. С вероятностью 0,954 оп­ределить пределы, в которых будут находиться средняя зольность угля в месторождении и доля угля с зольностью более 20%.

Решение. Средняя зольность угля в месторождении будет нахо­диться в пределах

 

Для определения границ генеральной средней вычислим предель­ную ошибку выборки для средней по формуле:

 

С вероятностью 0,954 можно утверждать, что средняя зольность угля в месторождении будет находиться в пределах 16% ± 1%, или 15%<  < 17%.

Доля угля с зольностью более 20% будет находиться в пределах

 

Выборочная доля определяется по формуле

где m , доля единиц, обладающих признаком:

   

Ошибку выборки для доли ( ) вычислим по формуле:

 

  

 

С вероятностью 0,954 можно утверждать, что доля угля с золь­ностью более 20% в месторождении будет находиться в пределах р = 10% ± 6%, или 4% <р< 16%.

В практике проектирования выборочного наблюдения возникает потребность в нахождении численности выборки, которая необхо­дима для обеспечения определенной точности расчета генеральных характеристик — средней и доли.

Предельная ошибка выборки, вероятность ее появления и вариа­ция признака предварительно известны.

При случайном повторном отборе численность выборки опреде­ляется по формуле

При случайном бесповторном и механическом отборе числен­ность выборки вычисляется по формуле