1.2 Ширина p-n перехода. Ёмкость p-n перехода.

 Из-за ухода основных носителей заря да, электронов из n - области в р - область и дырок из р- области в n - область, и в результате их рекомбинации, граница между р и  n полупроводни­ками обеднена носителями заряда, и её сопротивление велико по сравнению с сопротивлением остальных областей. Эта граничная область, обладающая большим сопротивлением, называется запорным слоем. По своей протяжённости запорный слой- это слой об­ласти пространственного заряда.

Ширина этой области зависит от концентрации донорных и акцепторных примесей в n – и  р- полупроводниках.

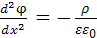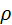Распределение потенциала в переходной области и ширину области объёмного заряда можно определить из решения уравне­ния Пуассона, связывающего потенциал поля с объёмной плотностью зарядов, создающих это поле:  , где     - объёмная плотность зарядов,

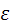 - относительная диэлектрическая проницаемость полупроводника, 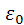- диэлектрическая проницаемость вакуума. Из решения _этого уравнения с учётом граничных условий на  контакте можно получить выражение для определения контактной разности

потенциалов: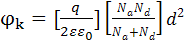  

откуда

 

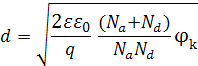
d-ширина p-n перехода, т.е. суммарная ширина отрицательно за­ряжённой области р- полупроводника и положительно заряжённой области n - полупроводника d=x_n+x_p. Здесь 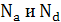 -концентрации акцепторных и донорных примесей соответственно.

Если концентрация примесей в одной области значительно больше чем в другой, например, 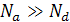 (так называемый несим­метричный p-n переход ), выражение для определения ширины p-n перехода упрощается и принимает вид:

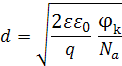
Так  как 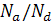= x_n/x_p, то npи  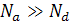    x_n>>x_p и ширина об­ласти объёмного заряда распространяется в полупроводник с меньшей концентрацией примеси. Из анализа выражения для опре­деления вытекает, что ширина области пространственного заря­да, т.е. ширина p-n  перехода тем больше, чем слабее легированы полупроводники, и наоборот, значение d тем меньше, чем больше концентрация донорных и акцепторных примесей. При  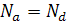получается симметричный p-n переход и области пространственного заряда одинаково удалены от границы контактов в обе стороны p-n перехода. Если же концентрация одной из примесей больше, тогда область пространственного заряда расположена в основном на стороне слаболегированного полупроводника. Приве­дённое выше выражение для ширины p-n перехода имеет место, ес­ли существует резкая граница между p и n - областями полупроводника. При плавных p-n переходах, когда концентрация при­месей от р- и n- областей меняется линейно, по закону  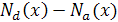=Aх, где А - градиент концентрации примесей, ширина p-n перехода может быть выражена так: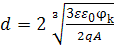

      Двойной электрический слой, имеющиеся в области p-n перехода можно уподобить обкладкам заряжённого плоского конденсатора и ёмкость такого перехода может быть определена по формуле ёмкости плоского конденсатора: С= S 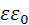/d, где S - площадь p-n перехода, d - ширина p-n перехода. Если к p-n переходу приложить внешнее электрическое поле, то в зависимости от направления этого поля оно или складывается с внутренним контактным по­лем или вычитается из него. При приложении к концам p-n - областей внешнего напряжения, всё оно будет падать на области объёмного заряда т.к. эта область обеднена носителями заряда и её сопротивление велико по сравнению с сопротивлением остальных участков. Если к р- области подключить плюс, к n-области минус от внешнего источника ЭДС, то знак внешней ЭДС противоположен знаку  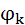и потенциальный барьер уменьшится, т.е. уменьшится ширина p-n перехода.  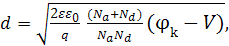при      .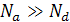

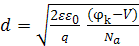Такая полярность внешнего напряжения называется прямой. При обратной полярности напряжения высота потенциального барьера растёт, ширина p-n перехода увеличивается (рис.1.2). Как уже отмечалось, в несимметричном p-n переходе это увеличение про­исходит в основном в сторону области с меньшей концентрацией примеси. Поскольку с изменением внешнего напряжения происходит и изменение ширины p-n перехода, то соответственно изменяется и ёмкость перехода. С учётом внешне го напряжения формула для расчета ёмкости имеет  вид: C=S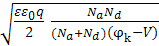

для случая 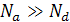    C=S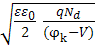        

    Эта  ёмкость        называется барьерной иди зарядной ёмкостью.

В отличие от барьерной ёмкости существует понятие диффузионная ёмкость p-n перехода, связанная с накоплением неоснов­ных носителей на границе p-n перехода  при прохождении тока в прямом направлений. Об этом будет сказано позже. Как видно из формулы для барьерной ёмкости,

ёмкость растет с увеличением концентрации примесей. Последняя формула часто используется для определения концентрации примеси по экспериментальной зависимости 1/C²=f(V), которая представляет собой прямую линию. Если напряже­ние на p-n переходе V = 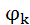 ,то 1/C² = 0. Таким образом можно эксперимен­тально измерить .

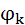В p-n переходе с линейным расп­ределением примеси, прямая линия получается для зависимости 1/C³=f(V), откуда можно определить А и   .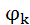

 

                               

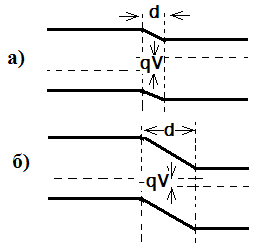
Рис.1.2. Изменение ширины  p-n перехода при приложении  прямого (а) и обратного (б) напряжения.