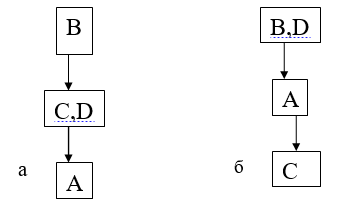
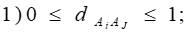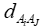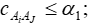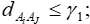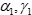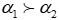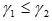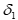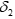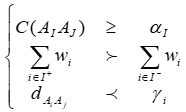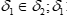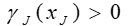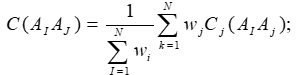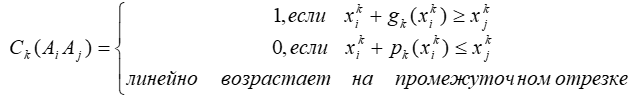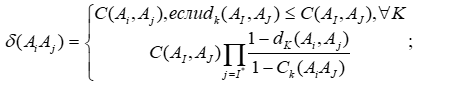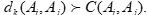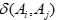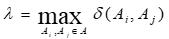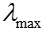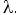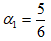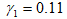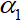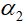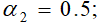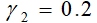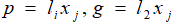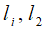|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Тема 9. Оценка многокритериальных альтернатив: методы ELECTRE
1. Конструктивистский подход 2. Два основных этапа 3. Свойства бинарных отношений 4. Метод ELECTRE1 .. Метод ELECTRE II . Метод ELECTRE III 5. Пример практического применения метода ELECTRE III 6. Некоторые сопоставления
1. Конструктивистский подход
В конце 60-х годов группа французских ученых во главе с профессором Б. Руа предложила новый подход к проблеме принятия решений при многих критериях. Название outranking approach, под которым он известен в мировой литературе, мало отражает его содержание. Мы будем называть его далее подходом, направленным на Разработку Индексов Попарного Сравнения Альтернатив (РИПСА). В настоящее время имеется много методов принятия решений, принадлежащих к данному подходу. Из них наиболее известна группа методов ELECTRE (Elimination Et Choix Traduisant la Realite - исключение и выбор, отражающие реальность) . Как и методы аналитической иерархии, методы РИПСА направлены на сравнение заданной группы многокритериальных альтернатив. Следовательно, методы РИПСА принадлежат к методам первой группы согласно приведенной в лекции 4 классификации. Прежде всего, следует подчеркнуть методологическое отличие подхода РИПСА от подходов MAUT и АНР. В рамках двух последних подходов неявно предполагается, что основные предпочтения ЛПР уже, в основном, сформированы до применения метода принятия решений. Следовательно, эти предпочтения могут быть получены от ЛПР «одномоментно» — при сравнениях оценок, назначении весов и т.д. Возможные уточнения введенных оценок осуществляются на этапе проверки чувствительности, т.е. на заключительном этапе применения метода. В отличие от этого при подходе РИПСА предполагается, что предпочтения ЛПР формируются при анализе проблемы, осуществляемом с помощью метода принятия решений. Следовательно, метод должен предъявлять ЛПР различные варианты решения проблемы в зависимости от тех или иных решающих правил. Эти правила формируются в виде индексов попарного сравнения альтернатив.
2. Два основных этапа
При подходе РИПСА принято различать два основных этапа : 1) этап разработки, на котором строятся один или несколько индексов попарного сравнения альтернатив; 2) этап исследования, на котором построенные индексы используются для ранжирования (или классификации) заданного множества альтернатив. Индексы попарного сравнения альтернатив в большинстве методов строятся на основе принципов конкорданса (согласия) и дискорданса (несогласия). В соответствии с этими принципами, альтернатива аi является, по крайней мере, не худшей, чем альтернатива Аj, если • «достаточное большинство» критериев поддерживает это утверждение (принцип согласия); • «возражения» по остальным критериям «не слишком сильны» (принцип малого несогласия).
3. Свойства бинарных отношений
Подход РИПСА основан на построении бинарных отношений. Поэтому следует дать некоторые определения. Бинарное отношение К, определенное на конечном множестве альтернатив А, называется (при • полным, если аi R Аj или Аj R Аi; . транзитивным, если Аi R Аj , Аj R Аk => аi R Аj; • полным порядком, если оно полное и транзитивное; • частичным порядком, если оно транзитивное, но не полное. Обозначим через Напомним, что отношение предпочтения ЛПР при сравнении альтернатив по одному критерию является полным порядком. При подходе РИПСА вводится понятие псевдокритерия. Псевдокритерием является тройка
предпочтение по сравнению с Аj;
имеет слабое предпочтение по сравнению с Аj. Альтернативы аi, Аj находятся в отношении безразличия по k-му критерию Функции р и g называются соответственно порогами безразличия и предпочтения. Бинарное отношение называется четким, если оно построено на основе критериев, и числовым (valued), если оно построено на основе псевдокритериев. Далее мы рассмотрим ряд методов, принадлежащих подходу РИПСА.
4. Метод ELECTRE I
Метод ELECTRE I был первым в семействе методов, принадлежащих к подходу РИПСА. В нем используются четкие бинарные отношения между альтернативами. Индексы согласия и несогласия строятся следующим образом. Каждому из N критериев ставится в соответствие целое число w, характеризующее важность критерия. Б. Руа предложил рассматривать w как число голосов членов жюри, поданное за важность данного критерия. Выдвигается гипотеза о превосходстве альтернативы аi над альтернативой Аj Множество I, состоящее из N критериев, разбивается на три подмножества: I+ — подмножество критериев, по которым аi предпочтительнее Аj; I= - подмножество критериев, по которым аi равноценно Аj; I- — подмножество критериев, по которым АJ предпочтительнее аi. Далее формулируется индекс согласия с гипотезой о превосходстве аi над Аj. Индекс согласия подсчитывается на основе весов критериев. В методе ELECTRE I этот индекс определяется как отношение суммы весов критериев подмножеств I+ и I= к общей сумме весов: Индекс несогласия dAB с гипотезой о превосходстве аi над Аj определяется на основе самого противоречивого критерия — критерия, по которому аj в наибольшей степени превосходит аi. Чтобы учесть возможную разницу длин шкал критериев, разность оценок Аj и Аi, относят к длине наибольшей шкалы: где : Укажем очевидные свойства индекса согласия. 3) CAiAj сохраняет значение при замене одного критерия на несколько с тем же общим весом. Приведем свойства индекса несогласия: 2) Введенные индексы используются при построении матриц индексов согласия и несогласия для заданных альтернатив. Отметим, что индекс несогласия может быть назван «вето», так как он как бы накладывает вето на сравнения. В методе ELECTRE I бинарное отношение превосходства задается уровнями согласия и несогласия. Если где Если же при этих уровнях сравнить альтернативы не удалось, то они объявляются несравнимыми. С методологической точки зрения, введение понятия несравнимости было важным этапом развития теории принятия решений. Если оценки альтернатив в значительной степени противоречивы (по одним критериям одна намного лучше другой, а по другим - наоборот), то такие противоречия никак не компенсируются и такие альтернативы сравнивать нельзя. Понятие несравнимости исключительно важно и с практической точки зрения. Оно позволяет выявить альтернативы с «контрастными» оценками как заслуживающие специального изучения. Отметим, что уровни коэффициентов согласия и несогласия, при которых альтернативы сравнимы, представляют собой инструмент анализа в руках ЛПР и консультанта. Задавая эти уровни (постепенно понижая требуемый уровень коэффициента согласия и повышая требуемый уровень коэффициента несогласия), они исследуют имеющееся множество альтернатив. При заданных уровнях на множестве альтернатив выделяется ядро недоминируемых элементов, которые находятся либо в отношении несравнимости, либо в отношении эквивалентности. При изменении уровней из данного ядра выделяется меньшее ядро и т.д. Аналитик предлагает ЛПР целую серию возможных решений проблемы в виде различных ядер. В конечном итоге можно получить и одну лучшую альтернативу. При этом значения индексов согласия и несогласия характеризуют степень «насилия» над данными, при которых делается окончательный вывод. Итак, основные этапы метода ELECTRE I можно представить следующим образом. I) Этап разработки индексов На основании заданных оценок двух альтернатив подсчитываются значения двух индексов: согласия и несогласия. Эти индексы определяют согласие и несогласие с гипотезой, что альтернатива Аi превосходит альтернативу Аj. Задаются уровни согласия и несогласия, с которыми сравниваются подсчитанные индексы для каждой пары альтернатив. Если индекс согласия выше заданного уровня, а индекс несогласия ниже, то одна из альтернатив превосходит другую. В противном случае альтернативы несравнимы. II) Этап исследования множества альтернатив Из множества альтернатив удаляются доминируемые. Оставшиеся образуют первое ядро. Альтернативы, входящие в ядро, могут быть либо эквивалентными, либо несравнимыми. Вводятся более «слабые» значения уровней согласия и несогласия (меньший по значение уровень согласия и больший уровень несогласия), при которых выделяются ядра с меньшим количеством альтернатив. В последнее ядро входят наилучшие альтернативы. Последовательность ядер определяет упорядоченность альтернатив по качеству.
5. Метод ELECTRE II
Этап разработки индексов
Так же, как в методе ELECTRE I в методе ELECTRE II используются четкие бинарные отношения между альтернативами. Индекс согласия подсчитывается тем же способом, что и в методе ELECTRE I . В методе ELECTRE II задаются два уровня для индекса согласия:
Ясно, что
Этап исследования множества альтернатив На заданном конечном множестве альтернатив А выявляются альтернативы, находящиеся в сильном, а затем - в слабом отношении предпочтения. Далее выявляется первое ядро, в которое входят недоминируемые альтернативы. Затем они удаляются из рассмотрения, и процедура повторяется снова уже для оставшихся альтернатив и т.д. Присваивая ранги альтернативам, входящим в соответствующие ядра, строим полный порядок на множестве альтернатив. Второй полный порядок строится аналогично первому, но начиная с класса худших альтернатив (недоминирующих другие) и переходя снизу вверх к лучшим альтернативам. Если два построенных порядка не слишком различны по упорядочению альтернатив, то на их основе строится средний порядок, который и предъявляется ЛПР. Это построение осуществляется на основе следующих правил: · AiPAj строго превосходит, если аi имеет лучший ранг в одном из порядков, и по крайней мере не худший в другом; · AiIAj (эквивалентны), если они имеют одинаковые ранги в двух полных порядках; · АiN Аj (несравнимость), если они имеют одно упорядочение в одном из порядков, противоположное - в другом.
6. Метод ELECTRE III
Этап разработки индексов В методе ELECTRE III используются псевдокритерии и числовые бинарные отношения. Задано N псевдокритериев и уровень вето Индексы согласия и несогласия вычисляются следующим способом:
Для каждой пары альтернатив Аi, Аk строится «числовое» бинарное отношение в следующем виде:
здесь I* — множество критериев, для которых Величину
Этап исследования альтернатив На этом этапе определяется сначала Устанавливается достаточно близкий к Далее для каждой альтернативы аi подсчитываются два индекса: · индекс «силы» — число альтернатив, доминируемых Аi, · индекс «слабости» - число альтернатив, доминирующих Аj Альтернативе Аi присваивается характеризующее ее число, равное разности индексов «силы» и «слабости». Затем строится сверху вниз первый полный порядок альтернатив аналогично тому, как это делается в методе ELECTRE II. Альтернативы с наибольшим значением Другой порядок определяется при подходе снизу вверх. На основе полных двух порядков строится средний, аналогично тому, как это делается в методе ELECTRE II. Отметим, что метод ELECTRE IV близок по идеям к методу ELECTRE III. Наиболее существенное отличие состоит в том, что в ELECTRE IV не используются веса критериев.
7. Пример
Обратимся к нашему примеру, используя метод ELECTRE I. Предположим, что в задаче выбора места для строительства аэропорта заданы альтернативы: А ($180 млн, 70 мин., 10 тыс.); С ($160 млн, 55 мин., 20 тыс.); В ($170 млн, 40 мин., 15 тыс.); В ($150 млн, 50 мин., 25 тыс.). Пусть веса критериев следующие: w1 = 3; w2 = 2; wз = 1. Сохраним те же длины шкал L1 = 100; L2 = 50; L3 = 45. Матрица индексов согласия приведена как табл. 6.1, а матрица индексов несогласия — как табл. 6.2.
Таблица 6.1 Индексы согласия для примера
Таблица 6.2 Индексы несогласия для примера
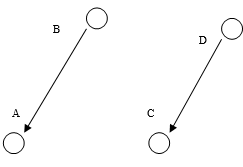
Зададим первые уровни согласия и несогласия: В первое ядро входят альтернативы В и Д , исключается альтернативы А и С, что легко устанавливается с помощью таблицы 6.1 и 6.2 Альтернативы В и D , входящие в ядро, несравнимы приведенных уровнях
Рис. 6.1 Выделение первого ядро Изменив уровни согласия и не согласия: Применив метод ELECTRE III для решения такой же задачи. Функции p и g зададим в следующем виде: Отметим, что мы не используем уровней вето.
Таблица 6.3. Значения постоянных величин
Матрица индексов согласия приведена как таб. 6.4.
Таблица 6.4. Матрица индексов согласия
Различие между матрицами, представленными таб. 6.1 и 6.4, связано с использованием иного способа подсчета индекса согласия. Результаты ранжирования альтернатив сверху вниз приведены на рис. 6.2, а снизу вверх – на рис.6.2,б. Результирующие ранги альтернатив представлены в табл. 6.5.
Рис.6.2. Результаты ранжирования альтернатив
Таблица 6.5. Результирующие ранги альтернатив
8. Пример практического применения метода ELECTRE III
Практическая задача состояла в выборе системы переработки отходов в одном из районов Улу имеется 17 муниципалитетов и проживает около 185 тыс. человек. Было необходимо выбрать систему для переработки 80 тыс тонн твердых отходов на период до 2010г. Рассматривались три основных способа переработки отходов: вывоз на мусорные поля, сжигание и переработка в компост. Кроме того, в качестве предлагалось создание 17 предприятий по переработке в каждом из муниципалитетов, одно централизованное предприятия и промежуточные варианты. Всего рассматривалось 22 альтернативы. В выборе принимали участие представители всех муниципалитетов – группа из 113 человека. По согласовано с членами группы было выбрано восемь критериев оценка альтернатив: 1) стоимость переработки тонны отходов; 2) техническая надежность; 3)общее воздействие на окружающую среду; 4)воздействие на здоровье жителей региона; 5)кислотные выбросы; 6)выбросы загрязненной воды; 7)число рабочих , занятых на предприятиях; 8) количество переработанных отходов. Для консультантов из Финляндии привлекательной особенностью метода ELECTRE III была возможность коллективного определения весов критериев. Каждый член группы из113 человек заполнял вопросник, в котором требовалось назначить вес от одного до семи баллов, каждому из критериев. Ответы усреднялись, и средние значения использовались при выборе. Разброс весов был основной для анализа чувствительности. В итоге была выбрана альтернатива, предусматривающая четыре поля орошения, четыре предприятия по выпуску компоста и одно предприятие по сжиганию мусора.
9. Некоторые сопоставления
В отличие от подходов аналитической иерархии и многокритериальной теории полезности с помощью подхода РИПСА невозможно осуществить компенсацию малых оценок альтернативы по одному критерию ее большими оценками по другому критерию. Введение уровней несогласия или порогов вето не позволяет объявлять альтернативу Аi при парном сравнении более предпочтительной, если по одному или нескольким критериям она существенно уступает альтернативе Aj. Индексы сравнения в методах ELECTRE III, IV и в ряде других методов этого семейства дают возможность учесть неточности в данных и измерениях, совершаемых экспертами. Однако подход РИПСА не гарантирует выполнения двух важных методологических требований: полноты сравнений и транзитивности. Появление отношения несравнимости означает, что в некоторых парах альтернатив нельзя выявить отношение предпочтения. Кроме того, известны случаи, когда в результирующих графах отношений между альтернативами появляются циклы. Авторы методом предлагают в этих случаях два выхода из положений: 1) альтернативы, входящие в цикл, объявляется эквивалентными; 2) выявляется «наиболее слабое » звено в цикле, и цикл размыкается. Хотя методы ELECTRE были первично предложены как эвристические, имеется немало работ по их аксиоматическому обоснованию. Сформировалось и доказано теоремы, характеризующие методы, принадлежности к подходу РИПСА . В частности, исследования показали, что проблема создания системы индексов, гарантирующих заданные желательные свойства метода, близка к проблеме построения правил коллективного выбора. Метода ELECTRE реализованы в виде систем поддержки принятия решений. Эти системы достаточно привлекательны для пользователей. Они разработаны в университете Paris – Dauphine лабораторией анализа и моделирования систем, помогающих в принятии решений . Выводы 1. Одним из первых подходов к сравнению многокритериальных альтернатив является подход, основной на определении бинарного отношения превосходства альтернатив по качеству (outranking relation). Этот подход реализован в виде совокупности методов ELECTRE. Метод ELECTRE позволяют определять для каждой пары альтернатив индексы согласия и несогласия с гипотезой, что одна из альтернатив превосходит другую. 2. При заданных уровнях согласия и несогласия две альтернативы могут находится в отношениях превосходства, эквивалентности и несравнимости. Последовательное выделение ядер позволяет частично упорядочить альтернативы по качеству. 3. В методах семейства ELECTRE можно выделить два основных типа: · этап разработки, на котором строятся индексы попарного сравнения альтернатив; · этап исследования, на котором построенные индексы используются для анализа заданного множества альтернатив. 4. Достоинством методом ELECTRE является поэтапность выявления предпочтение ЛПР в процессе назначения уровней согласия и несогласия и изучения ядер. Детальный анализ позволяет ЛПР сформировать свои предпочтения, определить компромиссы между критериями. Использование отношения несравнимости позволяет выделить пары альтернатив с противоречивыми оценками, остановится на ядре, выделение которого достаточно обоснованно с точки зрения имеющийся информации. 5. При применении методов семейства ELECTRE веса критериев могут отражать мнение группы экспертов, а не только мнение ЛПР.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||