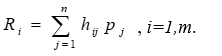Тема 5.  Принятие решений в условиях риска и неопределенности.                        

1. Принятие решений  в условиях  риска

2. Принятие решений в условиях неопределенности

3. Игровые методы обоснования решений

4. Методы коллективной экспертной оценки. Коллективная генерация идей.  Дельфийский метод

 

 

 

1. Принятие решений  в условиях  риска

 

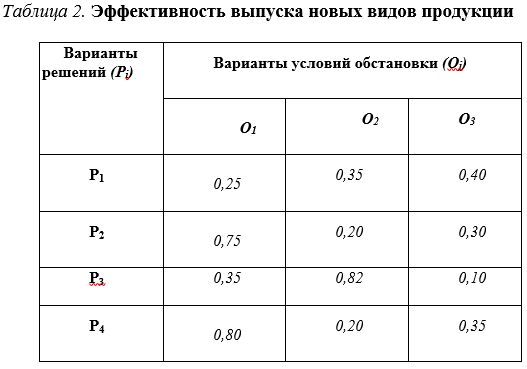
Элементы  неопределенности,  присущие функционированию и развитию  многих экономических  процессов,  обуславливают  появление  ситуаций,  не имеющих однозначного исхода (решения).

 Это обстоятельство  усложняет процесс  принятия  решений  в условиях  неопределенности  и предопределяет  необходимость  использования  соответствующих  методов, которые  дают  возможность  по заданным  целям  и ограничениям  получить  приемлемые для практики (оптимальные  или  рациональные)  управленческие  решения.

Как известно,  в зависимости  от  степени  неопределенности различают  ситуации   риска,   которые характеризуются  тем, что  в результате  каждого  действия  могут  быть  получены  различные  результаты,  вероятность  которых  известны  или может быть  оценена, т.е. каждой альтернативе соответствует  свое распределение вероятностей на множестве исходов.

На  методы  принятия  решений  в условиях  риска  накладывает  существенный  отпечаток  многообразие  критериев  и показателей,  посредством  которых  оценивается  уровень риска.

В самом  общем  виде  постановка и решение задачи  оптимизации  решений, принимаемых  в условиях риска, могут  быть представлены следующим  образом:

- имеется m  возможных  решений P₁,P₁,…,P_m;

- условия  обстановки ПР точно  неизвестны, однако  о них  можно  сделать n   предположений O₁, O₂, …., O_n;

- результат, так  называемый  выигрыш a_ij,  соответствующий  каждой  паре  сочетаний  решений P и  обстановке О,  может  быть  представлен в виде  таблицы эффективности (табл. 1.)

                       
 

 Выигрыши, указанные в табл.1., являются показателями эффективности решений.

Как отмечалось, выбор решения в условиях риска предпола­гает, что вероятности возможных вариантов обстановки изве­стны. Эти вероятности определяются на основе статистических данных, а при их отсутствии — на основе экспертных оценок.

Наличие выигрышей, являющихся показателями эффектив­ности решений при различных условиях обстановки, позволяет определить потери в результате принятия неоптимальных реше­ний - в случае, когда ожидаемое условие обстановки (имею­щее вероятностный характер) не произошло.

Порядок определения потерь будет рассмотрен нами в даль­нейшем в процессе решения конкретной задачи.

При выборе решения в качестве критерия риска использует­ся  показатель

R = hp

Предпочтение отдается решению, имеющему наименьший средневзвешенный показатель риска, определяемый как сумма произведений вероятностей различных вариантов обстановки на соответствующее им значение потерь:

                                                 

  h_ij- потери,p_j- вероятность.

Рассмотрим следующую задачу.

Пусть, например, предприятие готовится к переходу на новые виды продукции, при этом возможны четыре решения P₁ , P₂ , P₃ , P₄, каждому из которых соответствует определенный вид выпуска или их сочетание.

Результаты принятых решений существенно зависят от об­становки, которая в значительной мере не определена.

Пусть варианты обстановки характеризует структура спроса на новую продукцию, которая может быть трех типов: O₁, O₂, O₃.

Выигрыш, характеризующий относительную величину резуль­тата (доходы, прибыль и т.п.), соответствующий каждой паре сочетаний решений Р и обстановки О, представлен в табл. 2.

  

Из табл. 2 видно, что при обстановке O₃, решение P_{2 ,}  в три раза лучше, чем P₃,  а решение P₁, неодинаково для обстановки O₁ и O₃ , и т.д.

Необходимо найти такую стратегию (линию поведения) - решение Р, - которая по сравнению с другими является наи­более выгодной (целесообразной).

Для нахождения таких решений применяется специальный показатель потерь, который определяет, насколько выгодна при­меняемая нами стратегия в данной конкретной обстановке с учетом степени ее неопределенности. Потери рассчитываются как разность между ожидаемым результатом действий при на­личии точных данных обстановки и результатом, который мо­жет быть достигнут, если эти данные не определены

Например, если точно известно, что наступит обстановка O₁, следует принимать решение P₄ , которое в данной обстанов­ке обеспечит наибольший выигрыш - 0,80. Но поскольку точно не известно, какую обстановку ожидать, полагая, что наступит обстановка O₂ можно остановиться  на  решении P₃,  которое при данной обстановке дает выигрыш 0,82.

Если мы приняли решение P₃ (в надежде на обстановку O₂) а наступила обстановка O₁, то  мы получаем выигрыш, равный 0,35 (вместо 0,80 при принятии решения P₄). Таким  образам,  потери при принятии решения P₃ и наступлении обстановки O₁  (H₃₁) составляют 0,80 - 0,35 = 0,45.

В  общем  случае  потери H_ij,  соответствующие каждой  паре  сочетаний  решений P₁ и  обстановки О_j,    определяются как разность  между  максимальным  выигрышем и выигрышем по конк­ретному решению при данной обстановке, т.е. строится матрица сожалений:

 

Если a_ij представляют собой как в нашем случае «выигрыши» или «полезность», то элементы матрицы определяются следующим образом

                               

в противном случае, т. е. когда  a_ij- «потери»

                               

 

Так,  в соответствии  с данным  табл. 1.2, при   остановке О₁,  максимальный выигрыш составляет 0,80, а выигрыш по решениям Р₁ – Р₄  составляет соответственно: 0,25; 0,75; 0,35; 0,80

Тогда при обстановке О₁  потери по:

решению Р₁ (H_п) составят 0,80 - 0,25 = 0,55

решению Р₂ (H₂₁) составят 0,80 - 0,75 = 0,05

решению Р₃ (H₃₁) составят 0,80 - 0,35 = 0,45

решению Р₄ (H₄₁) составят 0,80 - 0,80 = 0.

 

Остальные значения  потерь при различных обстановках представлены в табл 3.

Приведенная таблица потерь существенно дополняет табли­цу эффективности.

Так, основываясь на таблице эффективности, можно прий­ти к выводу, что решение Р₁ при обстановке О₂ равноценно решению Р₄ при обстановке О₃.  Однако анализ указанных реше­ний с использованием данных таблицы 3 показывает, что они составляют соответственно 0,47 и 0,05.

 

 

 

 

Таблица 3. Величина потерь при выпуске новых видов продукции

 

Варианты решений  (Рi)	Варианты условий обстановки (Оi)
	O1	O2	O3
Р1	0,55	0,47	0,00
P2	0,05	0,62	0,10
P3	0,45	0,00	0,20
Р4	0,00	0,72	0,05

 

Такая существенная разница объясняется тем, что способ решения Р₁ при обстановке О₂ имеет эффективность 0,35, в то время как при этой же обстановке можно получить эффектив­ность до 0,82.

Решение Р₄ при обстановке О₃ реализует почти всю возмож­ную эффективность 0,35 из 0,40. Следовательно, решение Р₁ при обстановке О₂ значительно (почти в 10 раз) хуже, чем решение Р₄ при обстановке О_3.

Так, пусть вероятность первого варианта обстановки P₁ = 0,5, второго - 0,3 и третьего - 0,2, тогда показатель риска доя каждого из решений составит:

R₁ = 0,55 • 0,5 + 0,47 • 0,30 + 0,00 • 0,2 = 0,416;

R₂ =0,05-0,5   +0,62-0,3 + 0,10-0,2 = 0,231;

R_з = 0,45 • 0,5 +   0,00 • 0,3 + 0,30 • 0,2 = 0,285;

R₄ = 0,00 • 0,5 + 0,72 • 0,3 + 0,05 • 0,2 = 0,226;

Следовательно, решение Р₄ для данных условий является наи­менее рискованным.

Такой подход к принятию решений в условиях риска позво­ляет получить лишь вероятностные (средневзвешенные) резуль­таты анализа возможных вариантов. В отдельных случаях, в силу вероятностного характера экономических процессов, возможно получение результатов, отличных от планируемых (принятых на основе рассмотренного подхода). Вместе с тем, использование рассмотренного метода значительно повышает степень досто­верности оценок и результатов по сравнению с подходами к принятию решений без количественной оценки вариантов. Мож­но с уверенностью сказать, что при использовании указанного подхода улучшение результатов достигается посредством сокра­щения количества неудачных исходов в числе многократных хозяйственных циклов.

 

                          2.Принятие решений в условиях неопределенности

 

При принятии решений в условиях неопределенности, когда вероятности возможных вариантов обстановки неизвестны, может быть использованы ряд критериев, выбор каждого из ко­торых, наряду с характером решаемой задачи, поставленных целевых установок и ограничений, зависит также от склонно­сти к риску лиц, принимающих решения.

К числу классических критериев, которые используются при принятии решений в условиях неопределенности, можно отнести:

- принцип недостаточного обоснования Лапласа;

- максиминный критерий Вальда;

- минимаксный критерий Сэвиджа;

- критерий обобщенного максимина (пессимизма - оптимиз­ма) Гурвица.

Принцип недостаточного обоснования Лапласа используется в случае, если можно предположить, что любой из вариантов обстановки не более вероятен, чем другой. Тогда вероятности обстановки можно считать равными и производить выбор реше­ния так же, как и в условиях риска, — по минимуму средне­взвешенного показателя риска.

Следовательно, предпочтение следует отдать варианту, ко­торый обеспечивает минимум в выражении:

 

где n- количество рассматриваемых вариантов обстановки,p_j- вероятность появления обстановки O_j.

Рассмотрим выбор вариантов в условиях неопределенности с использованием принципа недостаточного обоснования Лап­ласа на исходных данных приведенного выше примера.

При учете трех вариантов обстановки (n = 3) вероятность каждого варианта составляет 0,33.

Тогда, с учетом приведенных данных о потерях для каждой пары сочетаний решений Р и обстановки О (табл. 3) и вероят­ности каждого варианта обстановки, равной 0,33, средневзве­шенный показатель риска для каждого из решений будет со­ставлять:

R₁= 0,55 • 0,33 + 0,47 • 0,33 + 0,00 • 0,33 = 0,3366; ;

R₂ =0,05 • 0,33 + 0,62 • 0,33 + 0,10 • 0,33 = 0,2541;

R₃ = 0,45 • 0,33 + 0,00 • 0,33 + 0,3 • 0,33 = 0,2475;

R₄ = 0,00 • 0,33 + 0,72 • 0,33 + 0,05 • 0,33 = 0,2541.

В качестве оптимального следует выбрать вариант реше­ния Р₃

 

Как видим, в исходном примере  наилучшим с точки зрения принятого критерия (средневзвешенного показа­теля риска) было бы решение Р₄.

Таким образом, изменение вероятности наступления вари­антов обстановки привело к изменению варианта решения, ко­торому следует отдать предпочтение.

Максиминный критерий Вальда используется в случаях, когда требуется гарантия, чтобы выигрыш в любых условиях оказы­вался не менее чем наибольший из возможных в худших усло­виях.

Наилучшим решением будет то, для которого выигрыш ока­жется максимальным из всех минимальных при различных ва­риантах условий.

Критерий, используемый при таком подходе, получил на­звание максимина. Его формализованное выражение

                                          

 

Как видим, в качестве исходных данных при выборе вариантов решений по критерию Вальда являются выигрыши а_ij , соответствующие каждой паре сочетаний решений Р и обстановки О.

Воспользуемся приведенным ранее примером (в частности, матрицей эффективности решений, представленной в табл. 2)  для иллюстрации выбора оптимального варианта по критерию Вальда.

      Минимальная отдача по вариантам выделена жирным цветом  в  табл. 4.

 

Таблица 4. Эффективность выпуска новых видов продукции

 

Варианты решений (Рi )	Варианты условий обстановки (Oi)
	O1	О2	O3
Р1	0,25	0,35	0,40
P2	0,75	0,20	0,30
P3	0,35	0,82	0,10
Р4	0,80	0,20	0,35

 

Из табл. 4 следует, что максимальный из минимальных ре­зультатов равен 0,25 и, следовательно, предпочтение необходи­мо отдать варианту Р₁ обеспечивающему этот результат.

Это максимальный гарантированный результат (выигрыш), который может быть получен в условиях имеющихся исходных данных. Выбрав решение Р₁, мы независимо от вариантов об­становки получим выигрыш не менее 0,25. При любом другом решении, в случае неблагоприятной обстановки, может быть получен результат (выигрыш) меньше 0,25.
    Так, при выборе решения Р₂ полученный выигрыш в зависи­мости от наступившего варианта обстановки будет колебаться от 0,2 до 0,75. Для решений Р₃ и Р₄ границы, в которых будет колебаться выигрыш, составят соответственно 0,10/0,82 и 0,20/0,80.

 

Данный критерий прост и четок, но консервативен в том смысле, что ориентирует принимающего решение на слишком осторожную линию поведения. Так, этот критерий никак не учитывает, что в случае принятия решения Р₁ (т.е. при ориента­ции на выигрыш 0,25) максимальный выигрыш не превышает 0,4. Однако, выбирая, например, решение Р₄, при гарантиро­ванном выигрыше 0,20 в случае благоприятной обстановки мож­но получить выигрыш, равный 0,80.

Поэтому критерием Вальда, главным образом, пользуются в случаях, когда необходимо обеспечить успех при любых возмож­ных условиях.

Рассмотрим минимаксный критерий Сэвиджа, который  используется в тех случаях, когда требуется в любых условиях избежать большого риска.

Этот критерий также относится к разряду осторожных. Одна­ко, в отличие от критерия Вальда, который направлен на полу­чение гарантированного выигрыша, критерий Сэвиджа мини­мизирует возможные потери.

Критерий минимального сожаления, предложенный Сэвиджем, состоит в применении  минимаксного критерия (независимо от того, какой характер имели элементы a_ij – «доходы» или  «потери») к матрице  сожалений:

                                                           min max h_ij

  

Здесь в качестве исходных данных при выборе решений выс­тупают потери (H_ij), соответствующие каждой паре сочетаний решений Р и обстановки О.

Для иллюстрации выбора по критерию Сэвиджа воспользу­емся приведенным выше примером (в частности, матрицей по­терь, представленной в табл. 3).

Максимальные потери по вариантам выделены в табл. 5 жирным шрифтом.

Таблица 5. Величина потерь при выпуске новых видов продукции

 

Варианты решений (Р1)	Варианты условий обстановки (О1)
	O1	О2	O3
Р1	0,55	0,47	0,00
Р2	0,05	0,62	0,10
Р3	0,45	0,00	0,30
Р4	0,00	0,72	0,05

 

Из табл. 5 следует, что минимальные из максимальных по­терь составляют 0,45 и, следовательно, предпочтение необходи­мо отдать варианту Р₃ обеспечивающему эти потери.

Выбор варианта решения Р₃ гарантирует, что в случае небла­гоприятной обстановки потери не превысят 0,45. В то время как для решений Р₁ Р₂ и Р₄ в случае неблагоприятной обстановки потери составят соответственно: 0,55; 0,62 и 0,72.

Основным исходным допущением этого критерия является предположение о том, что на наступление вариантов обстанов­ки оказывают влияние действия разумных противников (конку­рентов), интересы которых прямо противоположны интересам лица, принимающего решение. Поэтому, если у противников (конкурентов) имеется возможность получить какие-либо пре­имущества, то они ее обязательно используют. Это обстоятель­ство заставляет лицо, принимающее решение, обеспечить ми­нимизацию потерь от этих действий.

Критерий обобщенного максимина (пессимизма—оптимизма) Гурвица используется, если требуется остановиться между ли­нией поведения в расчете на худшее и линией поведения в рас­чете на лучшее.

В этом случае предпочтение отдается варианту решений, для которого окажется максимальным показатель О,  определяемый из выражения:

                     

где k — коэффициент, рассматриваемый как показатель опти­мизма , при k = 0 - линия поведения в расче­те на лучшее, при k = 1 - в расчете на худшее;

 

а_ij — выигрыш, соответствующий i- му решению при j-м ва­рианте обстановки.

Нетрудно убедиться, что при k = 1 критерий Гурвица совпа­дает с критерием Вальда, т.е. ориентацией на осторожное пове­дение. При k = 0 - ориентация на предельный риск, так как большой выигрыш, как правило, сопряжен с большим риском. Значения k между 0 и 1 являются промежуточными между рис­ком и осторожностью и выбираются в зависимости от кон­кретной обстановки и склонности к риску лица, принимающе­го решение.

В табл. 6 приведены значения показателя G для различ­ных вариантов решений в зависимости от величины коэффици­ента k.

 

Таблица 6. Значение показателя G для различных  k

Варианты решений (Рi)	Значение коэффициента k
	0,00	0,25	0,50	0,75	1,00
Р1	0,400	0,362	0,325	0,287	0,250
Р2	0,750	0,612	0,475	0,337	0,200
Р3	0,820	0,640	0,460	0,280	0,100
Р4	0,800	0,650	0,500	0,350	0,200
Оптимальное решение	Р3	Р4	Р4	Р4	Р1

 

Как видим, с изменением коэффициента k изменяется вари­ант решения, которому следует отдать предпочтение.

 

Нами рассмотрены наиболее общие (классические) методы, которые позволяют обосновывать и принимать решение при нео­пределенности экономических данных и ситуаций, недостатке фактической информации об окружающей среде и перспектив­ных ее изменениях.

Следует отметить, что разработанные экономической теори­ей и практикой способы и приемы решения задач в условиях риска и неопределенности не ограничиваются перечисленными методами. В зависимости от конкретной ситуации в процессе анализа используются и другие методы, способствующие реше­нию задач, связанных с минимизацией риска.

Некоторые из них, в частности, основаны на использование среднеквадратического отклонения  и коэффициента вариации (V) как меры риска.

 

Критерий, основанный на байесовском подходе.

В рамках нашего курса  рассмотрим весьма простой формализованный метод решения задач на принятие решений в ус­ловиях неопределенности, который основан на так называемом «байесовском подходе».

Прежде всего, рассмотрим типовой пример задачи на принятие решений, которая может быть решена этим методом.

Перед группой бурильщиков, осуществляющей разведку неф­тяных месторождений,  периодически встает вопрос, бурить ли ей скважину в определенном месте или нет.

При этом заранее неизвестны некоторые обстоятельства: стоимость бурения, запасы нефти на которые можно рассчитывать (в частности, результат может быть нулевым), стоимость эксплуатации скважины и т.д.

Для принятия решения можно заказать различную информа­цию, позволяющую принять решение более обоснованно: результат сейсмической разведки (это стоит достаточно дорого), заказать кар­ту данной местности из космоса (это стоит еще дороже) и т.д. В простейшем случае можно принять решение без использования до­полнительной информации.

В зависимости от результатов бурения можно рассчитывать на получение определенной прибыли, которая является случайной ве­личиной, и задается соответствующим законом распределения.

Если рассмотреть несколько подобных разных задач, можно, не вникая в содержательные особенности, выделить несколько об­щих этапов их решения:

 

• определение в рамках содержательной постановки задачи перечня (группы) событий, которые могут произойти

• составление списка доступных возможностей сбора инфор­мации, постановки эксперимента

• определение упорядоченной во времени последовательно­сти событий, в исходах которых можно получить определенную информацию, и последовательности действий, которые мы можем предпринять

• оценка полезности доступных действий

• определение вероятности каждого неопределенного (имеющего вероятностную природу) события

В качестве основного формального математического инстру­мента рассматриваемого метода используется так называемое «дерево решений» (диаграмма решений).

«Дерево решений» - это граф, содержащий вершины двух ти­пов. К первому типу относятся вершины, которые соответствуют моментам принятия некоторых частных решений человеком (эти вершины будем обозначать квадратиками), к другому типу - вер­шины, соответствующие проявлению случайной природы некоторых событий (эти вершины будем обозначать кружочками).

Можно использовать другое определение, дополняющее пер­вое. «Дерево целей» - это структура задачи в виде хронологически увязанных выборов (моментов принятия решений), которые должен делать человек, решающий задачу на принятие решений, и выбо­ров, определяемых случаем (случайным механизмом).

Продемонстрировать использование рассматриваемого метода и его основного рабочего инструмента - «дерево целей» можно на примере типовой задачи, сформулированной в терминологии урн (терминология, привычная в теории вероятностей).

 

Имеется  N  урн, каждая из которых может быть одного из двух типов - Q1 или Q2. Известно, что 80% урн принадлежат к ти­пу Q1, и 20%  урн - к типу Q2.

В каждой урне находятся 10 шаров (красные и черные). Рас­пределение красных и черных шаров различно в зависимости от типа урны - в урнах типа Q1   4 красных  и 6 черных шаров, в урнах типа Q2   9 красных и 1 черный шар.

Человеку предлагается сыграть в игру. Он случайным образом выбирает одну из  N   урн,  и должен решить, к какому типу принад­лежит выбранная им урна.

Если человек угадывает тип урны, то он выигрывает некото­рую сумму денег, если не угадывает - проигрывает.

У участника игры имеются варианты получить некоторую ин­формацию перед тем, как определить тип урны. За дополнительную плату (8 единиц) можно случайным образом вынуть 1 шар из выбранной урны. За дополнительную плату в 12 единиц можно вы­нуть 2 шара из выбранной урны. За дополнительную плату в 9 еди­ниц можно вынуть 1 шар и решить вынуть ли ещё один шар за 4.5 единиц. При этом шар, вынутый первым, может быть возвращен в урну или нет (возможны варианты) и т.д.

В результате человек может принимать решение, выбирая из следующих вариантов:

• отказаться от игры

• без дополнительной информации определить тип урны

(решение ЕО)

• вынуть один шар из выбранной урны и после этого опре­делить тип урны (решение Е1)

• вынуть два шара из выбранной урны и после этого опреде­лить тип урны (решение Е2)

• вынуть один шар из выбранной урны и решить, выбирать ли ещё один шар. После получения необходимой инфор­мации определить тип урны (решение ЕЗ).

Если участник игры определяет тип урны Q1, то он выигры­вает 40 единиц в случае «истинности», и проигрывает 20 единиц в случае «ложности» утверждения.

Если участник игры определяет тип урны Q2, то он выигры­вает 100 единиц в случае истинности, и проигрывает 5 единиц в случае «ложности» утверждения.

Для использования дерева в решении,  необходимо определить распределение вероятностей для возможных вариантов развития событий. Некоторые распределения вероятностей задаются в условиях задачи. Например, в нашей задаче задаются:

P(Q1) - вероятность выбора урны типа Q1, (P(Q1) = 0.8)

P(Q2) - вероятность выбора урны типа Q2, (P(Q2) = 0.2)

P(R/Q1) - вероятность выбрать красный шар при условии вы­бора урны типа Q1 (P(R/Q1) = 0.4)

P(B/Q1) - вероятность выбрать черный шар при условии вы­бора урны типа Q1 (P(B/Q1) = 0/6)

P(R/Q2) - вероятность выбрать красный шар при условии вы­бора урны типа Q2 (P(R/Q2) = 0.9)

P(B/Q2) - вероятность выбрать черный шар при условии вы­бора урны типа Q2 (P(B/Q2) = 0.1)   

Нам необходимо определить ещё четыре величины:

P(Q1/R), P(Q1/B), P(Q2/R), P(Q2/B), соответственно вероятно­сти выбора урны типа Ql (Q2) при условии, что был вынут крас­ный (черный) шар. Эти вероятности не заданы, их можно найти с помощью известной формулы Байеса.

P(Q1/R) = P(Q1)*P(R/Q1) / (P(Q1)*P(R/Q1)+P(Q2)*P(R/Q2)) =

= 0.8*0.4 / (0.8*0.4 + 0.2*0.9) = 0.64

P(Q1/B) = P(Q1)*P(B/Q1) / (P(Q1)*P(B/Q1)+P(Q2)*P(B/Q2) =

= 0.8*0.6 / (0.8*0.6 + 0.2*0.1) = 0.96

P(Q2/R) = P(Q2)*P(R/Q2) / (P(Q1)*P(R/Q1)+P(Q2)*P(R/Q2)) =

= 0.2*0.9 / 0.5 = 0.36

P(Q2/B) = P(Q2)*P(B/Q2) / (P(Q1)*P(B/Q1)+P(Q2)*P(B/Q2)) =

= 0.2*0.1 / 0.5 = 0.04

По известной формуле полной вероятности определим значе­ние безусловной вероятности достать красный (черный) шар:

P(R ) = P(Q1)*P(R/Q1) + P(Q2)*P(R/Q2) =

= 0.8*0.4 + 0.2*0.9 = 0.5

P(B) = 0.5.

Следует иметь в виду, что равенство вероятностей P(R ) и Р(В) определяется нашими исходными данными (при других исход­ных данных равенства, естественно, не будет).

                          3. Игровые методы обоснования решений

 

Особый, очень большой и разнообразный класс составляют задачи на принятие решений в условиях неопределенности, когда имеется сознательное противодействие «противника». Эти задачи характеризуются тем, что в них участвуют две или более конкури­рующих   стороны,   преследующие   противоположные   цели (конфликтные ситуации).

Методы решения таких задач достаточно сложны и рассмат­риваются в специальном разделе математики - Теория игр.

Введем некоторые понятия и определения:

Игра - упрощенная схематизированная модель конфликтной ситуации, где конкурирующие стороны соблюдают некоторые пра­вила игры.

Правила игры регламентируют:

• возможные варианты действия игроков

• объем информации каждой стороны о поведении другой стороны

• результат игры, к которому приводит любая совокупность ходов (чаще всего результат игры характеризуется число­вой величиной)

Игра развивается во времени, т.е. имеется последовательность действий игроков (игроки делают свои ходы).

Ход - выбор одного из предусмотренных правилами игры дей­ствий и его осуществление.

Различают личные и случайные ходы.

Личный ход - сознательный выбор одного из возможных дей­ствий и его осуществление.

Случайный ход - выбор из числа возможностей, осуществляе­мый с помощью механизма случайного выбора (бросание монеты, выбор карты и т.д.) в соответствии с законом распределения.

Стратегия игрока - совокупность правил, определяющих вы­бор варианта действий при каждом личном ходе в зависимости от ситуации, сложившейся в процессе игры.

Если число стратегий конечное, то считается, что игра - ко­нечная.

Оптимальная стратегия - стратегия, которая при много­кратном повторении игры обеспечивает данному игроку макси­мально возможный средний выигрыш (минимально возможный сред­ний проигрыш).

 

                                3.1. Платежная матрица

Для проведения простейшего анализа игровых задач на при­нятие решения используется так называемая платежная матрица.

Рассмотрим конечную игру, в которой участвуют два игрока А и В. Игрок А имеет m стратегий (Al, A2, ..., Am), а игрок В - n стратегий (Bl, B2, ..., Вn).

Предположим, что при выборе игроком А стратегии Ai и иг­роком В стратегии Bj игрок А получает выигрыш aij. Тогда можно составить платежную матрицу, в которой строки соответствуют стратегиям игрока А, столбцы - стратегиям игрока В, а элементы матрицы - соответствующим выигрышам игрока А.

 

 

 

	B1	B2	…	Вn
A1	a11	а12	...	а1n
A2	а21	а22	…	а2n
...	...	...	...	...
Am	am1	аm2		аmn

 

Рассмотрим простой пример (Игра «поиск»).

Игрок А - прячется, игрок В - ищет игрока А. В распоряжении иг­рока А есть два убежища. Если игрок В «находит» игрока А (с од­ной попытки), то игрок А платит ему 1 руб. Если Игрок В не «находит» игрока А, то он платит игроку А 1руб. Платежная матрица для такой игры будет иметь вид:

 

	B1	B2
A1	-1	1
A2	1	-1

 

Анализ этой простой игры показывает, что, используя пла­тежную матрицу, можно получить далеко нетривиальные выводы:

• если играть только один раз, то вообще нельзя говорить об оптимальной стратегии

• если играть многократно, то игроку А нельзя придержи­ваться какой-либо одной стратегии или чередовать их в каком-либо определенном порядке. В этом случае игрок В со временем поймет закономерность использования стратегий и начнет постоян­но выигрывать.

• игроку А необходимо использовать случайный механизм выбора стратегий (стратегии A1 и A2 должны быть равновероятны).

В нашем примере игрок А должен использовать «смешанную стратегию», когда отдельные чистые стратегии (Al, A2) череду­ются случайным образом.

Пример 2.  (Игра «Пальцы»).

Игроки А и В «выбрасывают» одновременно до 3-х (1, 2 или 3) пальцев. Игрок А выигрывает (величина выигрыша равна сумме «выброшенных» пальцев), если сумма четная и соответственно проигрывает, если сумма - нечетная.                                                               Для данной игры платежная матрица имеет вид:

 

	В1	В2	В3
A1	2	-3	4
A2	-3	4	-5
A3	4	-5	6

 

Анализ этой платежной матрицы позволяет заключить:

• для каждой стратегии игрока А у игрока В есть лучшая страте­гия (для A1 - В2, для A2 - ВЗ, для A3 - В2)

• аналогично у игрока А есть лучшая стратегия игры против игро­ка В

• игрокам А и В необходимо пользоваться «смешанными страте­гиями»

 

              3.2. Нижняя и верхняя цена игры. Принцип минимакса

 

Рассмотрим некоторую игру, определяемую нижеприведенной платежной матрицей, и рассмотрим случай использования в этой игре «чистых» стратегий.

 

	В1	В2	...	Вn
A1	a11	а12		а1n
A2	а21	а22		а2n
...
Am	am1	аm2		аmn

 

Дополним платежную матрицу столбцом с элементами a₁, a₂, …, a_m, где    a_i = min a_ij     (минимизация по j) и строкой с элементами     b₁, b₂, …, b_n,

где b_j = max a_ij.минимизация по i ).  

a = max a_i    или a = max min a_ij - нижняя цена игры - так называемый максимин.

Оказывается, что при любом поведении игрока В игрок А имеет выигрыш не меньший, чем a. Таким образом a это оценка снизу для результата игры игрока А, если в игре исполь­зуются «чистые» стратегии.

Аналогичные рассуждения можно провести для игрока В и ввести     

  b = min b_j     или      b = min max a_ij  - называют минимакс или верхняя цена игры. Придерживаясь «чистой» стратегии, соответствующей минимаксу, игрок В может быть уверен, что проиграет не больше  b.

Принцип, определяющий игрокам выбор максиминной и ми­нимаксной стратегий, называется принципом минимакса.

Рассмотрим игру, характеризующуюся «платежной матрицей»:

 

 

 

	В1	В2	ВЗ
А1	2	-3	4	-3
А2	-3	4	-5	-5
A3	4	-5	6	-5
	4	4	6

 

Для этой игры a = -3, b = 4.

Максиминная стратегия игрока А гарантирует, что игрок А проиграет не более 3 руб., минимаксная стратегия игрока В гаран­тирует, что он проиграет не больше 4 руб.

Для рассматриваемой игры минимаксные стратегии неустой­чивы.

Действительно, пусть Игрок В выбрал стратегию В1, тогда, поняв это, игрок А выберет A3 и будет выигрывать 4 руб. На это игрок В может ответить стратегией В2 и будет выигрывать 5 руб. На это игрок А ответит стратегией А2 и будет выигрывать 4 руб. и т.д.

В нашем случае соответствующие минимаксные стратегии иг­роков неустойчивы, и могут быть изменены после поступления ин­формации о поведении противника.

Однако, существуют игры, для которых значения максимина и минимакса совпадают. При этом минимаксные стратегии игроков А и В («чистые стратегии») являются устойчивыми стратегиями.

В платежной матрице такой игры имеется элемент, который является одновременно минимальным в своей строке и максималь­ным в соответствующем столбце. Такой элемент называют «седловой точкой», а соответствующую игру - игрой с «седловой точкой».

Для игры с «седловой точкой» минимаксные стратегии игро­ков А и В являются оптимальными стратегиями, т.е. если один игрок придерживается своей минимаксной стратегии, то для другого игрока не может быть выгодным отклоняться от своей минимаксной стратегии.

Для игры с «седловой точкой» минимаксные стратегии обла­дают устойчивостью.

Одним из фундаментальных результатов «Теории игр» являет­ся доказательство факта, что «игры с полной информацией» явля­ются играми с «седловой точкой» (к таким играм относятся, напри­мер, шашки, шахматы, крестики-нолики и т.д.).

«Игры с полной информацией» - это игры, в которых каждый игрок при каждом личном ходе знает результаты всех предыдущих ходов - как личных, так и случайных. Таким образом, доказано, что любая «игра с полной информацией» имеет «седловую точку» и, следовательно, оптимальное решение в «чистых стратегиях». Это сильный результат, если учитывать, что класс игр с полной ин­формацией достаточно велик.

Другим интересным фундаментальным результатом «Теории игр» является утверждение, что для каждой «конечной игры» мож­но в классе «смешанных стратегий» найти пару устойчивых опти­мальных стратегий для игроков А и В, обладающих свойством -если один из игроков придерживается своей оптимальной страте­гии, то другому не может быть выгодно отступать от своей (здесь оптимальные стратегии смешанные).

Рассмотренный материал из «Теории игр» является очень кратким введением, позволяющим почувствовать специфику задач этого раздела математики, получить представление об используемом аппарате и сложности задач данной области.

 

4. Методы коллективной экспертной оценки. Коллективная генерация идей.  Дельфийский метод.

 

Если ранее рассмотренные модели и методы решения претен­довали на вполне определенные классы задач на принятие реше­ний, то методы коллективной экспертной оценки могут быть ис­пользованы для решения любых задач на принятие решений.

Такая целевая универсальность методов коллективной экс­пертной оценки, естественно, должна сочетаться со значительной неконкретностью используемых алгоритмов решения задач. Так оно и есть на самом деле.

Сущность методов коллективной экспертной оценки состоит в определении согласованности мнений экспертов по вопросам, требующим принятия решений.

В данном разделе под термином эксперт будем понимать специалиста в определенной области очень высокой квалификации, так что он имеет право делать свои заключения, не всегда обосно­вывать их.

Методы коллективной экспертной оценки, как правило, включают следующие этапы:

• создание рабочих групп, в функции которых входит прове­дение опроса, обработка материалов и анализ результатов коллек­тивной экспертной оценки. Рабочая группа назначает экспертов (количество экспертов - 10-150), которые дают ответы на постав­ленные вопросы

• разработка вопросов (необходимо обеспечить однознач­ность понимания вопросов), которые будут представлены экспертам

• обработка материалов коллективной экспертной оценки, которые характеризуют обобщенное мнение и степень согласован­ности индивидуальных оценок экспертов. Окончательная оценка определяется как среднее в определенном смысле суждение экспер­тов.

 Метод «мозгового штурма»

Основное назначение метода «мозгового штурма» - поиск но­вых идей на основе интуититвного мышления.

В основе метода лежит тезис - «большое число идей включа­ет по крайней мере несколько хороших идей».

Основные условия для реализации метода:

• сформулировать проблему в основных терминах

• не объявлять ни одну идею ошибочной

• поддерживать каждую идею, даже если её осуществление предполагается в далеком будущем

• постоянно поддерживать и подбадривать участников для создания свободных взаимоотношений » стремиться к тому, чтобы высказывания участников были четкими и сжатыми

• критика предыдущих выступлений не допускается

• каждый участник может выступать несколько раз, но не подряд

Важный этап метода - систематизация идей, который вклю­чает:

• составление перечня всех высказанных идей, определение дублирующих и дополняющих идей, формирование комплексных идей

• объединение идей в группы, согласно выделенным призна­кам

• упорядочение идей в группах от более общих к более част­ным.

Часто используется этап деструкции, который включает оценку идей на основе критерия практической реализуемости. Ка­ждая идея подвергается всесторонней критике со стороны участни­ков «мозговой атаки». При этом могут появляться новые идеи. На этом этапе в группу участников «мозговой атаки» привлекаются вы­сококвалифицированные специалисты.

Далее идет оценка критических замечаний и составление списка практически применимых идей.

В результате составляется список идей, которые не опроверг­нуты критикой.

 Метод Дельфи.

Этот метод был в свое время разработан известной Rand Cor­poration для решения задач долгосрочного прогнозирования. Сущность метода заключается в следующем:

• разрабатываются подробные вопросники для ведущих спе­циалистов и экспертов

• вопросы в анкетах составляются так, чтобы ответы на них имели какую-либо количественную характеристику

• опросы экспертов проводятся в несколько туров, в ходе которых вопросы и ответы все более уточняются

• предусматривается ознакомление с результатами опроса всех участников опроса после каждого тура

• использование методов математической статистики для обработки результатов опросов и получения обобщающих характеристик.

С помощью «метода Дельфи» успешно выявляются преобла­дающие суждения авторитетных специалистов по анализируемому вопросу