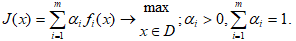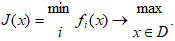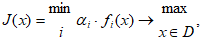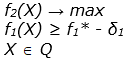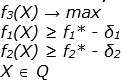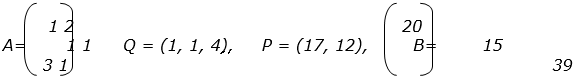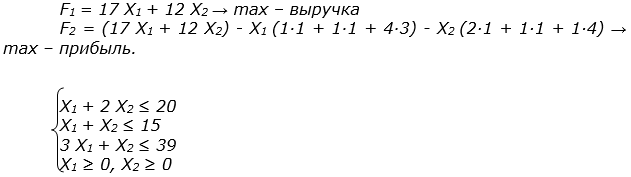|
| ||||||||||||||||||
|
Тема 6. Многокритериальные решениея при обънетивныъ моделях .1. Модели 2. Многокритериальность 3. Разные типы проблем 4. Многокритериальные модели принятия решений в условиях определенности. 5. Методы многокритериальной оптимизации. 6. Методы Многокритериального выбора на основе дополнительной информации
Для анализа и исследования реальных объектов исследователи создают их копии или упрощенные образы, описанные с помощью формального языка. Целями создания модели являются обычно: использование её в решении задач, которые трудно решать на реальном объекте; лучшее понимание объекта; построение улучшенного объекта путем внесения изменений в модель. Естественным требованием к модели является её идентичность реальному объекту. Мы изучаем внешний мир, создавая модели. Мы улучшаем искусственные системы, используя их модели. В обоих случаях роль моделей чрезвычайно велика. Необходимо подчеркнуть, что модели, применяемые в естественных науках, отличаются от моделей, используемых в экономике. Экономические модели описывают процессы, в которых важную роль играют люди. Совершаемые ими действия и их результаты находят отражение в модели. Модели, описывающие поведение людей, активно используются в исследовании операций. Под исследованием операций понимают применение математических количественных методов для обоснования решений во всех областях человеческой деятельности. Основными этапами решения любой задачи в исследовании операций являются: 1. построение модели 2. выбор критерия оптимальности 3. нахождение оптимального решения Для подхода исследования операций характерны следующие особенности. 1. Используемые модели носят объективный характер. Модель отражает существующую реальность, т. е. опираясь на одни и те же данные, различные специалисты-аналитики должны получать одинаковые результаты. 2. Руководитель получает научно-обоснованное решение. Аналитик исследует реальную ситуацию и пытается построить адекватную модель. В этой работе сам ЛПР чаще всего не нужен. Он дает заказ и получает готовое решение. 3. Существует объективный критерий успехов в применении методов исследования операций. Если проблема, требующая решения, ясна и критерий определен, то аналитический метод сразу показывает насколько новое решение лучше старого.
2. Многокритериальность
При широком применении методов исследования операций аналитики стали сталкиваться с задачами, где имеется не один, а несколько критериев оценки качества решения. Опыт использования методов математического моделирования и компьютеров в различных областях человеческой деятельности привел к пониманию многих принципиальных трудностей, возникающих при их внедрении в реальную практику. Оказалось, что ЛПР, при принятии решения учитывает огромное число показателей, которые только в редких случаях удаётся представить в виде одного критерия. Стало очевидно, что методы исследования операций, которые успешно применялись при моделировании различных ситуаций, совершенно недостаточны для решения более сложных проблем, которые по сути своей являются многокритериальными. Многие факторы (социальные, организационные, политические, психологические и т. д.), имеющие существенное влияние на альтернативы не поддаются формализации. Такого рода задачи имеют следующую характерную особенность – модель, описывающая множество допустимых решений объективна, но качество решения оценивается по многим критериям. Для выбора наилучшего варианта решения необходим компромисс между оценками по разным критериям. В условиях задачи отсутствует информация, позволяющая найти такой компромисс. Следовательно, он не может быть определен на основе объективных расчетов. Анализ многих реальных практических проблем, с которыми сталкивались специалисты, естественным образом привел к появлению класса многокритериальных задач. Задачи со многими критериями имеют следующие особенности: -Задача имеет уникальный, новый характер – нет статистических данных, позволяющих обосновать соотношения между различными критериями -На момент принятия решения принципиально отсутствует информация, позволяющая объективно оценить возможные последствия выбора того или иного варианта решения. Это может быть сделано лишь людьми на основе их опыта и интуиции.
3. Разные типы проблем
Подходы исследования операций и принятия решений существенно различаются, так как они направлены на принципиально разные проблемы принятия решений, существующие в окружающем нас реальном мире. Так, в одной классификации, предложенной в 1958 году Г. Саймоном и А. Нотоэллом, выделяются так называемые хорошо и слабо структурированные проблемы. Хорошо структурированные, или количественно сформулированные проблемы – те, в которых существенные зависимости хорошо определены и могут быть выражены в числах или символах, получающих численные оценки. Неструктурированные проблемы, содержащие лишь описание важнейших ресурсов, признаков и характеристик, количественные зависимости между которыми совершенно неизвестны. Слабоструктурированные, или смешанные проблемы, которые содержат как качественные, так и количественные элементы. Можно сказать, что типичные проблемы исследования операций являются хорошо структурированными. По иному обстоит дело в многокритериальных задачах. Здесь часть информации, необходимой для полного и однозначного определения к решению, принципиально отсутствует. Поэтому такие проблемы являются слабоструктурированными. Слабоструктурированные и неструктурированные проблемы исследуются в рамках научного направления, называемого принятием решений при многих критериях. Появление многокритериальности привело к принципиальному изменению характера решаемой задачи.
4. Многокритериальные модели принятия решений в условиях определенности.
Рассмотрим следующую модель задачи ПР: X- множество альтернатив;
Таким образом, мы здесь предполагаем, что каждому решению Соответствует единственный элемент
«Качество» или «полезность» исхода y , а тем самым и соответствующего решения x оценивается несколькими ( m) числами в соответствии с зависимостями fi. Для определенности будем полагать, что функции fi-максимизируются. С помощью суперпозиции
Мы имеем возможность непосредственно оценивать качество самого решения x т. е. считаем, что задано отображение В результате мы приходим к очень распространенной в приложениях многокритериальной модели принятия решений, или задаче многокритериальной оптимизации вида
5. Методы многокритериальной оптимизации.
Вначале рассмотрим традиционные «инженерные» методы многокритериальной оптимизации, сводящие задачу (1) к некоторой ее однокритериальной версии. Рассматривая задачу (1), отметим, что в идеальном случае можно вести поиск такого решения, которое принадлежит пересечению множеств оптимальных решений всех однокритериальных задач. Однако такое пересечение обычно оказывается пустым множеством, поэтому приходится рассматривать так называемое «переговорное» множество эффективных решений (оптимальных по Парето). Некоторые частные критерии могут противоречить друг другу, другие действуют в одном направлении, третьи – индеферентны, безразличны друг другу. Поэтому процесс решения многокритериальных задач неизбежно связан с экспертными оценками, как самих критериев, так и взаимоотношений между ними. Известен ряд методов решения задач многокритериальной оптимизации. Рассмотрим некоторые из них: Метод главного критерия. В данном методе в качестве целевой функции выбирается один из функционалов fi, например fi, наиболее полно с точки зрения исследователя отражающий цель ПР. Остальные требования к результату, описываемые функционалами учитываются с помошью введения необходимых дополнительных ограничений. Таким образом, вместо задачи (1) решается другая, уже однокритериальная задача вида Формально получили более простую задачу поиска максимума функционала fi на новом допустимом множестве D0. Добавились ограничения вида Метод линейной свертки. Он основан на линейном объединении всех частных целевых функционалов
Весовые коэффициенты ai могут при этом рассматриваться как показатели относительной значимости отдельных критериальных функционалов fi. Метод максиминной свертки. Обычно применяется в форме
Здесь, в отличие от метода линейной свертки, на целевой функционал При необходимости нормировки отдельных частных целевых функционалов может быть использована «взвешенная» форма максиминного критерия:
где весовые коэффициенты ai удовлетворяют требованиям (2). Метод последовательных уступок. Он применяется в случае, когда частные критерии могут быть упорядочены в порядке убывания их важности. Предположим, что все частные критерии максимизируются и пронумерованы в порядке убывания их важности. Находим максимальное значение f1* первого по важности критерия в области допустимых решений путем решения однокритериальной задачи. Затем, исходя из практических соображений и принятой точности, назначается величина допустимого отклонения (экономически оправданные уступки) критерия f1 и находится максимальное значение второго критерия f2* при условии, что значение первого критерия не должно отклоняться от своего максимального значения более чем на величину допустимой уступки, т. е. решается задача:
Снова назначается величина уступки
Аналогичные процедуры повторяются до тех пор, пока не будет выявлено максимальное значение последнего по важности критерия fm.
Рассмотрим следующий пример: для выпуска 2-х видов продукции используются 3 вида ресурсов. Известна матрица норм расхода А, цены Q на ресурсы, цены реализации P продукции и запасы В ресурсов.
На основе исходной информации могут быть определены 2 критерия: прибыли и выручка с двумя переменными Х1 – выпуск продукции 1-го вида и Х2 – выпуск продукции 2-го вида. Тогда задача может быть записана следующим образом:
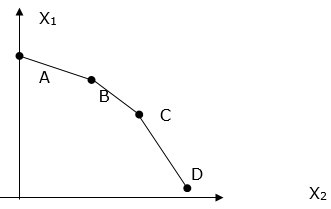
Графически множество допустимых решений может быть изображено следующим образом:
Значения критериев в угловых точках заданы в таблице:
Окончательный выбор останется за ЛПР. Критерий оптимальности итальянского экономиста В. Парето применяется при решении таких задач, когда оптимизация означает улучшение одних показателей при условии, чтобы другие не ухудшались. Определение: Решение задачи (1) Х* fi (X) >= fi (X*), i = 1, m, (3) Причем хотя бы для одного значения i имеет место строгое неравенство. Определение: Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности (т. е. улучшить хотя бы один из них, не ухудшая остальных), принято называть областью Парето, или областью компромиссов, а принадлежащие ей решения эффективными, или оптимальными по Парето. В общем случае эффективные решения не эквивалентны друг другу, так что про два оптимальных по Парето решения нельзя сказать, какое из них лучше. Поэтому при решении многокритериальных задач необходимо дополнительное изучение эффективных решений. В рассмотренном выше примере точки В и С определяют решения оптимальные по Парето. Сказать однозначно какое из этих решений лучше нельзя, поэтому необходимо получить от ЛПР дополнительную информацию для принятия решения. 6. Методы многокритериального выбора на основе дополнительной информации Решением многокритериальной задачи, сформулированной выше, является соответствующее множество Парето- множество недоминируемых по Парето альтернатив. Это множество может оказаться достаточно обширным, а пользователя обычно интересует выбор какого-то «наилучшего» варианта или небольшого их числа. Если какая-либо дополнительная информация о задаче отсутствует, то множество Парето – это лучшее, что можно предложить. Однако при наличии дополнительной информации о системе предпочтений пользователя могут быть применены различные методы сужения исходного множества альтернатив – более сильные, чем методы, основанные на доминировании по Парето. Весьма часто исходной информацией для таких методов выступает само множество Парето и ставится задача его сужения с целью выбора одной или нескольких альтернатив в качестве окончательного результата. Метод t – упорядочения. Пусть решается многокритериальная задача (1). Будем предполагать, что все критериальные функции fi отражают «полезность» объекта с позиций различных критериев и являются соизмеримыми в том смысле, что значения каждой критериальной функции изменяются в одних и тех же пределах [a, b]:
Таким образом, мы предполагаем, что оценочные шкалы критериев являются числовыми и одинаковыми. Требование, связанное с необходимостью приведения всех числовых шкал к единому промежутку достигается с помощью, например, следующих простых преобразований:
Здесь max fi , min fi- максимальные и минимальные значения fi соответственно. Новые оценочные функции Итак, пусть критериальные функции соизмеримы и удовлетворяют условиям (4). Определение. Нормированные критерии fi и fj называются равноценными ( fi = fj), если всякие две векторные оценки Z, W, где одинаковы по предпочтительности при любом Таким образом, если, например, два школьника оцениваются по четырем предметам и имеют оценки (которые необходимо максимизировать) Z = (5,4,4,3), W = (5,5,3,3)
то при условии равноценности критериев f2, f3 приведенные векторные оценки будут одинаковыми по предпочтительности, т.к. 4+4=5+3, а остальные оценки совпадают. Следовательно, если критерии fi и fj равноценны, то можно «забрать» единиц у частной оценки zj и «передать» их частной оценке zi. При этом получим векторную оценку, одинаковую с исходной по предпочтительности. Если в приведенном выше примере считать, что оценка Z предпочтительнее, чем W, то естественно предположить, что критерий f3 важнее критерия f2. Определение. Критерий fi более важен, чем критерий fj (что записывается в виде fi > fj), если векторная оценка менее предпочтительна, чем оценка где с частной оценки zj на частную оценку zi приводит к улучшению ситуации, если fi >fj. На основе выше приведенной операции переноса единиц с одной частной оценки на другую частную оценку происходит сокращение множества Парето решаемой многокритериальной задачи. Рассмотрим пример. Путь Z = (1; 0,5; 0,1; 0,2), W = (0,4; 0,9; 0,1; 0,2)
и пусть утверждается, что критерий f1важнее, чем f2: f1 > f2. Эти векторные оценки, очевидно, несравнимы по Парето. Рассмотрим оценку W' = (0,8; 0,5; 0,1; 0,2)
полученную из W с помощью переноса 0,4 единиц со второй позиции в первую. Согласно определению имеем И, поскольку имеем То естественно считать Методы упорядочения альтернатив, основанные на рассмотренной процедуре переноса (transfer) c учетом ординальной (порядковой) информации пользователя, называются методами t- упорядочения. Частным случаем изложенного метода t- упорядочения является метод, предложенный В.В. Подиновским (метод П - упорядочения). Он основан на том, что мы имеем возможность переставлять численные значения оценок между равноценными и неравноценными критериями. Например, пусть дана векторная оценка Z=(5,10,6) и известно, что f1 > f2. Тогда по Подиковскому оценка Недостатком метода П – упорядочения является его недостаточная «мощность». Например, пусть даны векторные оценки Z=(7,9,6), W=(5,10,6)
при наличии ординальной информации f1> f2. Эти оценки, очевидно, несравнимы по Парето. Несравнимы они и по методу П – упорядочения (никакие перестановки численных значений оценок между f1 и f2 не приводят к их сравнимости по Парето). В то же время легко видеть, что согласно методу t- упорядочения для W'=(6,9,6) полученной из W с помощью переноса одной единицы со второй позиции в первую, мы имеем
и, следовательно, | |||||||||||||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | ||||||||||||||||||
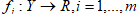
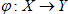
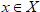
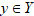
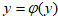
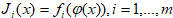
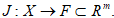
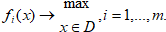 (1)
(1)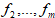 ,
, 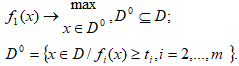
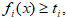
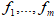 в один:
в один: