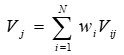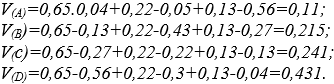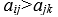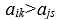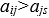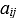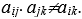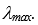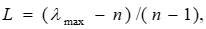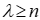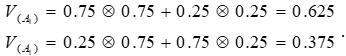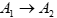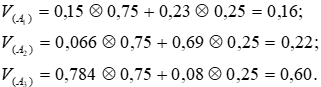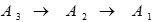Тема 8. Оценка Многокритериальных альтернатив: подход аналитической иерархии

 
         1.Основные этапы подхода аналитической иерархии

2.     Структуризация

3.     Попарные сравнения

4.      Определение наилучшей альтернативы

5.     Проверка согласованности суждений ЛПР

6.      Контрпримеры и противоречия

 

 

 

                   1. Основные этапы подхода аналитической иерархии

 

Подход аналитической иерархии (Analytic Hierarchy  Process  - АНР) широко известен в настоящее время. Мы можем найти в журналах оживленные дискуссии между противника­ми и сторонниками этого подхода.

При подходе MAUT одни и те же усилия ЛПР по построе­нию функции полезности могут быть затрачены при большом и малом числе альтернатив. Не всегда такой подход является обоснованным. В случае небольшого числа заданных альтерна­тив (задачи первой группы) представляется разумным напра­вить усилия ЛПР на сравнение только заданных альтернатив. Именно такая идея лежит в основе метода АНР .

Постановка задачи, решаемой с помощью метода АНР, за­ключается обычно в следующем.

Дано: общая цель (или цели) решения задачи; N критериев оценки альтернатив; n  альтернатив.

Требуется: выбрать наилучшую альтернативу. Площадки А Площадка Площадка Площадка D

 

 

Подход АНР состоит  из совокупности этапов.

1.  Первый этап заключается в структуризации задачи в ви­де иерархической структуры с несколькими уровнями:

                               Цели - критерии - альтернативы.

2.  На втором этапе ЛПР выполняет попарные сравнения
элементов каждого уровня. Результаты сравнений переводятся
в числа при помощи специальной таблицы (см. далее).

3.  Вычисляются  коэффициенты  важности для  элементов
каждого уровня. При этом проверяется согласованность сужде­ний ЛПР.

4.  Подсчитывается количественный индикатор качества каждой из альтернатив и определяется наилучшая альтернатива.

Рассмотрим эти этапы подробнее применительно к основ­ному методу АНР, разработанному Т. Саати, используя для иллюстрации,  пример выбора площадки для строительства аэропорта.

 

2.Структуризация

 

Предположим, что комиссия по выбору места постройки аэропорта предварительно отобрала из нескольких возможных четыре варианта: А, В, С, В. Тогда структура решаемой задачи может быть представлена в виде, показанном на рис. 1.

Варианты имеют следующие оценки по критериям: А (180; 70; 10),

В (170; 40; 15), С (160; 55; 20), D (150; 50; 25).

 

Попарные сравнения

 

При попарных сравнениях в распоряжение ЛПР дается шкала словесных определений уровня важности, причем каж­дому определению ставится в соответствие число (табл. 1).

При сравнении элементов, принадлежащих одному уровню иерархии, ЛПР выражает свое мнение, используя одно из при­веденных в табл. 1 определений. В матрицу сравнения зано­сится соответствующее число. При желании ЛПР может ис­пользовать четные целые числа, выражая промежуточные уров­ни предпочтения по важности. Матрица сравнений критериев выбора площадки для аэропорта приведена в табл. 2.

 

Рис. 1. Иерархическая схема проблемы выбора места для аэропорта

 

 

Таблица. 1.    Шкала относительной важности

Уровень важности	Количественное значение
Равная важность Умеренное превосходство Существенное или сильное превосходство Значительное (большое) превосходство Очень большое превосходство	1 3 5 7 9

 

Таблица   2.     Матрица сравнений для критериев

Критерий	C 1,   Стои­мость	C 2  , Время в пути до центра города	С3   , Количество людей под­вергающихся шумовым воздействиям	Собствен­ный вектор	Вес крите­рия
С1   Стоимость	1	5	3	2,47	0,65
С2 Время в пути до центра города	1/5	1	3	0,848	0,22
Сз Количество   людей, подвергающихся шумовым воздействиям	1/3	1/3	1	0,48	0,13

 

Матрица соответствует следующим предпочтениям гипоте­тического ЛПР: критерий «Стоимость» существенно превосхо­дит критерий «Время в пути» и умеренно превосходит крите­рий «Количество людей, подвергающихся шумовым воздейст­виям»; критерий С₂ умеренно превосходит критерий С_з.

На нижнем уровне иерархической схемы сравниваются за­данные альтернативы (конкретные площадки) по каждому критерию отдельно. Приведем эти сравнения в табл. 3 - 5.

Таблица  3. Сравнение по критерию С₁

Альтернатива	А	В		С	D	Собственный вектор	Вес
А	1	0,2		0,14	0,11	0,23	0,04
В	5	1		0,33	0,2	0,76	0,13
С	7		3	1	1/3	1,63	0,27
В	9		5	3	1	3,4	0,56

 

Таблица 4. Сравнение по критерию С₂

Альтернатива	А	В	С	D	Собственный вектор	Вес
А	1	0,11	0,2	0,14	0,23	0,05
В	9	1	3	1	2,28	0,43
С	5	0,33	1	1	1,14	0,22
D	7	1	1	1	1,63	0,3

 

Таблица   5. Сравнение по критерию Сз

Альтернатива	А	В	С	D	Собственный вектор	Вес
А	1	3	5	9	3,4	0,56
В	0,33	1	3	7	1,63	0,27
С	0,2	0,33	1	5	0,76	0,13
D	0,11	0,14	0,2	1	0,23	0,04

 

4. Вычисление коэффициентов важности

 

Таблицы 2 - 5 позволяют рассчитать коэффициенты важности соответствующих элементов иерархического уровня. Для этого нужно вычислить собственные векторы матрицы, а затем пронормировать их. Формула для этих вычислений: из­влекается корень n-й степени (n — размерность матрицы срав­нений) из произведений элементов каждой строки.

Так, по табл. 2 определяются коэффициенты важности критериев. В предпоследнем столбце таблицы приведены зна­чения собственных векторов. Нормирование этих чисел дает: w₁ = 0,65; w₂ = 0,22; w_з = 0,13, где w_i — вес i-го критерия.

Таким же способом на основе табл. 3 - 5 можно рас­считать важность каждой из площадок по каждому из крите­риев. В таблицах приведены веса соответствующей площадки по каждому из критериев.

 

                         3. Определение наилучшей альтернативы

 

Синтез полученных коэффициентов важности осуществля­ется по формуле

                               

где   V_j-  показатель качества j-й альтернативы;  w_i -  вес  i-го критерия; V_ij - важность j-й альтернативы по i-му критерию.

Для четырех площадок проведенные вычисления позволя­ют определить:

 Итак, альтернатива D — наилучшая.

 

                                       4.Проверка согласованности суждений ЛПР

 

При заполнении матриц попарных сравнений человек мо­жет делать ошибки. Одной из возможных ошибок является на­рушение транзитивности: из  ,  может не следо­вать а  (   - элементы матрицы попарных сравнений). Во-вторых, возможны нарушения согласованности численных су­ждений:

Для обнаружения несогласованности предложен подсчет индекса согласованности сравнений, осуществляемый по мат­рице парных сравнений. Изложим алгоритм этого подсчета.

1.      В матрице парных сравнений суммируются элементы
каждого столбца.

2.   Сумма элементов каждого столбца умножается на соот­ветствующие нормализованные компоненты вектора весов, оп­ределенного из этой же матрицы.

3.      Полученные числа суммируются, значение суммы обозначаем как 

4.   Находим индекс согласованности

                         

5.   где n - число сравниваемых элементов (размер матрицы). За­метим, что для кососимметрической матрицы .

6.   Подсчитывается среднее значение индекса согласованности R  для кососимметричных  матриц, заполненных случайным образом. Так, для матрицы размера n=7 индекс R=1,32, а для матрицы размера n=8 индекс R=1,41.

 

N	1	2	3	4	5	6	7	8	9	10
R	0	0	0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49

 

6. Вычисляется отношение согласованности:

T=L/R

При применении метода желательным считается уровень

Т <= 0,1. Если значение Т превышает этот уровень, рекомендует­ся провести сравнения заново.

 

Система поддержки принятия решений Expert Choice

 

Популярность метода аналитической иерархии определя­ется, не в последнюю очередь, высоким качеством компьютер­ной системы Expert Choice, реализующей этот метод. Эта сис­тема поддержки принятия решений выпускается как коммер­ческий продукт. Она поддерживает построение иерархии на всех уровнях, дает примеры построенных иерархий.

Система допускает ввод информации при осуществлении парных сравнений в качественном и количественном виде, а также в графическом виде. Сразу после заполнения матрицы следует проверка согласованности суждений. ЛПР может полу­чить совет повторить сравнения, если индекс Т превышает зна­чение 0,1. На каждом этапе работы система может привести примеры и дать необходимые разъяснения для пользователя.

 

5. Контрпримеры и противоречия

 

Метод аналитической иерархии возник как эвристическое средство сравнения и выбора альтернатив. Хотя, предпринима­ются усилия разработать аксиоматические основания метода, в большинстве публикаций он предстает как эвристический под­ход, апеллирующий к здравому смыслу пользователя.

Отметим, что подход АНР имеет большее число практиче­ских предложений, чем другие многокритериальные методы. Ежегодно проводятся конференции пользователей этого метода. Одновременно с этим публикуются статьи с анализом сущест­венных методологических недостатков основного метода АНР. Найдено, что введение новой альтернати­вы может в общем случае привести к изменению отношений предпочтений между двумя другими альтернативами (rank reversals).

Приведем иллюстративный пример. Пусть имеются два критерия и две альтернативы: A₁, А₂. В табл. 6 представлены сравнения, позволяющие вычислить веса критериев.

           Таблица 6.  Матрица сравнения для критериев

Критерий	С1	С2	Собственный вектор	Вес
С1	1	3	1,732	0,75
С2	0,333	1	0,577	0,25

 

В табл. 7 и  8 даны сравнения альтернатив по критериям.

 

Таблица 7. Сравнение по критерию С₁

Альтернатива	а1	А2	Собственый вектор	Вес
а1	1	3	1,732	0,75
А2	0,333	1	0,577	0,25

 

 

 

 

 

Таблица 8. Сравнение по критерию С₂

Альтернатива	A1	А2	Собственный вектор	Вес
A1	1	0,333	0,577	0,25
А2	3	1	1,732	0,75

 

Подсчитаем показатели качества альтернатив:

Следовательно, .

 Добавим альтернативу A_з, сравнения с которой представле­ны в табл. 9 и 10.

Таблица 9.  Сравнение по критерию C₁

Альтернатива	A1	А2	Аз	Собственный вектор	Вес
а1	1	3	0,14	0,754	0,15
А2	0,333	1	0,11	0,333	0,066
Аз	7	9	1	3,98	0,784

 

 

Таблица 10. Сравнение по критерию C₂

Альтернатива	а1	А2	Аз	Собственный вектор	Вес
а1	1	0,333	3	1	0,23
А2	3	1	9	3	0,69
Аз	0,333	0,11	1	0,333	0,08

 

Подсчитаем показатели альтернатив:

 

Следовательно,

Добавление A_з привело к изменению отношения между альтернативами A₁  и  А₂.