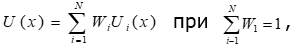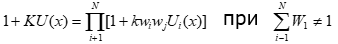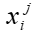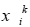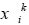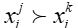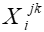Тема 7. Оценка многокритериальных альтернатив: многокритериальная теория полезности

1. Снова об этапах процесса принятия решений

2. Различные группы задач принятия решений

3. Многокритериальная теория полезности (MAUT)

4.Метод SMART - простой метод многокритериальной оценки

5.Первый эвристический метод

6. Веса критериев

7. Как люди назначают веса критериев

8.Практическое применение

1. Снова об этапах процесса принятия решений

В первых темах были определены три основных этапа процесса принятия решений: поиск вариантов решения (альтернатив), изобретение новых альтернатив, выбор наилучшей из группы альтернатив. Все эти этапы, безусловно, встречаются в достаточно сложных реальных ситуациях принятия решений. Мы можем представить себе политика, подготавливающего законопроект для рассмотрения парламентом. Изучая проблему, политический деятель обращается к истории, анализирует современную ситуацию. Зная точки зрения политических партий, представленных в парламенте, он ищет вариант законопроекта, достаточно приемлемый для других и решающий, с его точки зрения, поставленную задачу. Наконец, сравнивая несколько вариантов законопроекта, исходящих от различных авторов, он оценивает их по совокупности критериев (эффективность, затраты, влияние на различные социальные группы, реализуемость и т. д.) и выбирает наилучший.

Если мы обратимся к существующим методам принятия решений, то увидим, что подавляющее большинство этих методов предназначено для решения задач, которые Г. Саймон относит к третьему этапу — к сравнению заданных альтернатив и к выбору наилучшей из них. Легко понять, почему задачи первого и второго этапов не рассматриваются в рамках различных теорий выбора. Задачи эти в основных своих чертах неформализованы и решаются благодаря навыкам и умениям консультанта и ЛПР. Если в процессе принятия решений всегда переплетены наука и искусство, то на первых двух этапах научные методы не играют основной роли. На третьем этапе задача предстает уже в достаточно определенном виде.

В этой, в следующих двух и в восьмой лекции мы рассмотрим наиболее известные методы анализа решений, ориентированные на задачи, при решении которых используются модели субъективного характера. При решении таких задач строится не модель окружающей нас реальности, а модель желаний, предпочтений, политики человека, принимающего решения. Описанные далее методы построения таких моделей реализованы в виде компьютерных систем поддержки принятия решений.

2. Различные группы задач принятия решений

Представим в самых общих чертах группы задач принятия решений.

Задачи первой группы

Дано: группа из n альтернатив (вариантов решения проблемы) и N критериев, предназначенных для оценки альтернатив. Предположим, что каждая из альтернатив имеет оценку по каждому из критериев, полученную либо от экспертов, либо на основании объективных расчетов.

Требуется: построить решающие правила на основе предпочтений ЛПР, позволяющие: выделить лучшую альтернативу;

• упорядочить альтернативы по качеству;

• отнести альтернативы к упорядоченным по качеству классам
решений.

Задачи второй группы

Дано: группа из N критериев, предназначенных для оценки любых возможных альтернатив; альтернативы либо заданы частично, либо появляются после построения решающего правила.

Требуется: на основании предпочтений ЛПР построить решающие правила, позволяющие:

• упорядочить по качеству все возможные альтернативы;

• отнести все возможные альтернативы к одному из нескольких (указанных ЛПР) классов решений.

Примером задач первой группы является многокритериальная оценка имеющихся в продаже товаров, например телевизоров или стиральных машин. Здесь все возможные альтернативы заданы, критерии определены ЛПР; оценки реальных альтернатив по критериям дают, как правило, эксперты. От ЛПР требуется построить правило сравнения объектов, имеющих оценки по многим критериям (например, сравнить стиральные машины на основании таких оценок, как цена, долговечность, стоимость эксплуатации, надежность, возможность ремонта и т.д.).

Примером задач второй группы является построение правила принятия решений для государственного или частного фонда, распределяющего ресурсы на научные исследования. Проекты проведения исследований еще не поступили, но критерии оценки и решающее правило должны быть определены заранее. Обычно таких проектов много, и можно предположить, что они будут достаточно разнообразны по оценкам. Критерии и решающее правило определяет ЛПР. Затем уже поступают проекты, которые оцениваются экспертами по заданным критериям. Решающее правило позволяет сразу же получить целостную оценку проекта.

Представленные выше две группы задач становятся весьма близкими, при рассмотрении в рамках первой задачи большого числа достаточно разнообразных (по своим оценкам) альтернатив. Но при малом числе заданных альтернатив методы решения задач первой и второй групп существенно различаются.

Пример. В силу благоприятных обстоятельств жители одного из городов некой страны стали чаще выезжать за границу. Существующие аэропорты, расположенные около города (назовем его городом М), не соответствовали по своим возможностям новому потоку пассажиров. Возникла необходимость в построении еще одного аэропорта около города М.

Правительство этой страны назначило комиссию по выбору места для аэропорта, которая приступила к работе. Были обследованы различные площадки около города, где постройка аэропорта нужного размера представлялась возможной. После многочисленных дискуссий комиссия определила три основных критерия для оценки вариантов расположения аэропорта.

1. Стоимость постройки. Желательно построить аэропорт
с заданной пропускной способностью за наименьшую возможную цену.

2. Расстояние от города. Желательно, чтобы поездка пассажиров от аэропорта в город и обратно занимала наименьшее время.

3. Минимальное шумовое воздействие. Количество людей, подвергающихся нежелательным шумовым воздействиям, должно быть, по возможности, минимальным.

Легко заметить, что все эти критерии противоречивы. Постройка аэропорта на большом расстоянии от города потребует, вероятно, меньших затрат, хотя время поездки будет больше. Противоречивы также критерии расстояния от города и числа людей, подвергающихся шумовым воздействиям. Как выбрать площадку для аэропорта? Как найти компромисс между критериями?

Подчеркнем некоторые особенности рассматриваемой задачи. Прежде всего, она может быть отнесена к так называемым неструктурированным задачам. Если задачи с объективными моделями (см. предыдущую лекцию) находятся как бы «на границе» с задачами исследования операций, то задачи, похожие на приведенную в нашем примере, «расположены» существенно дальше от этой границы. Хотя все критерии имеют вполне ясное объективное содержание, а оценки по критериям — количественное выражение, нет единой количественной модели, описывающей проблему в целом. Есть лишь набор из трех субъективно (комиссией) определенных критериев. Необходимо выбрать ту из заданных альтернатив (место для строительства), где достигается наиболее предпочтительный, с точки зрения комиссии, компромисс между критериями. Для решения таких задач строятся модели, описывающие предпочтения ЛПР (в данном случае комиссии), применение которых позволяет сделать лучший выбор.

Эти модели строятся по-разному в различных научных школах в области принятия решений. В этой главе мы представим широко известный подход многокритериальной теории полезности (МАUТ).

3. Многокритериальная теория полезности (MAUT)

Научное направление MAUT (Multi - Attribute Utility Theory) отличают следующие особенности:

· строится функция полезности, имеющая аксиоматическое
(чисто математическое) обоснование;

· некоторые условия, определяющие форму этой функции,
подвергаются проверке в диалоге с ЛПР;

· обычно решается задача из второй группы, а полученные результаты используются для оценки заданных альтернатив.

Основные этапы подхода MAUT

Представим этапы решения задачи при подходе MAUT.

1. Разработать перечень критериев.

2. Построить функции полезности по каждому из критериев.

3. Проверить некоторые условия, определяющие вид общей
функции полезности.

4. Построить зависимость между оценками альтернатив по
критериям и общим качеством альтернативы (многокритериальная функция полезности).

5. Оценить все имеющиеся альтернативы и выбрать наилучшую.

Аксиоматическое обоснование

Точно так же, как и классическая теория полезности , MAUT имеет аксиоматическое обоснование. Это означает, что выдвигаются некоторые условия (аксиомы), которым должна удовлетворять функция полезности ЛПР. В случае если условия удовлетворяются, дается доказательство существования функции полезности в том или ином виде. В MAUT эти условия можно разделить на две группы. Первая группа — аксиомы общего характера, идентичные тем, которые использовались в теории полезности.

1. Аксиома полноты, утверждающая, что может быть установлено отношение между полезностями любых альтернатив: либо одна из них превосходит другую, либо они равны.

2. Аксиома транзитивности: из превосходства полезности альтернативы А над полезностью альтернативы В и превосходства полезности В над полезностью следует превосходство полезности альтернативы А над полезностью альтернативы С.

Для соотношений между полезностями альтернатив А, В, С, имеющими вид

Аксиома 3. Oснована на предположении, что функция полезности непрерывна и что можно использовать любые малые части полезностей альтернатив.

Вторая группа условий специфична для МАUТ. Они называются аксиомами (условиями) независимости, позволяющими утверждать, что некоторые взаимоотношения между оценками альтернатив по критериям не зависят от значений по другим критериям.

Приведем несколько условий независимости.

1. Независимость по разности. Предпочтения между двумя альтернативами, отличающимися лишь оценками по порядковой шкале одного критерия С₁, не зависят от одинаковых (фиксированных) оценок по другим критериям С₂, ..., С_N.На первый взгляд, это условие кажется естественным и очевидным. Но возможны случаи, когда оно не выполняется. Так, в статье П. Хампфриса приведен следующий пример: выбор автомобиля. При примерно одинаковой цене ЛПР предпочитает большую по размеру машину. Однако его предпочтение меняется на обратное, когда он узнает, что у машины не гидравлическая, а механическая коробка передач, что усложняет управление.

2. Независимость по полезности. Критерий С₁ называется
независимым по полезности от критериев С₂, ..., С_N, если поря
док предпочтений лотерей, в которых меняются лишь уровни
критерия С₁, не зависит от фиксированных значений по другим
критериям. Напомним, что определение лотереи было дано в
лекции 2. Как мы увидим далее, лотереи используются при построении функций полезности по отдельным критериям.

3. Независимость по предпочтению является одним из наиболее важных и часто используемых условий. Два критерия С₁ и С₂ независимы по предпочтению от других критериев С₃, .., С_N, если предпочтения между альтернативами, различающимися лишь оценками по С₁, С₂, не зависят от фиксированных значений по другим критериям.

Приведем пример нарушения условия независимости по предпочтению - выбор дачи для летнего отдыха (табл. 1). Вполне возможно, что альтернатива А предпочтительнее альтернативы В, если по критерию «Расстояние от города» оба варианта имеют оценку «Дача расположена недалеко от города». В то же время, если оба варианта имеют по последнему критерию оценку «Дача расположена далеко от города», вариант В может оказаться предпочтительнее варианта А.

Таблица 1. Задача выбора дачи для летнего отдыха

Альтернатива

Критерий

Альтернатива

Качество дачи

(комфортность)

Наличие магазина

недалеко от дачи

Расстояние

от города

A

В

Хорошее

Среднее

Нет магазина

Есть магазин

Первые два условия независимости относились к независимости одного критерия от остальных, третье условие — к независимости пары критериев от прочих.

Судя по литературе, отсутствуют примеры зависимости трех и большего числа критериев от остальных, которая не проявлялась бы в нарушении условия независимости по предпочтению. По мнению известных ученых Г. Фишера и Д. Винтерфельда , появление такой зависимости «неопределенно по своей природе и трудно обнаружимо». В связи с этим понятно особое внимание, уделяемое проверке условия независимости по предпочтению.

Основные теоремы

Если аксиомы первой группы и некоторые условия независимости выполнены, то из этого следует строгий вывод о существовании многокритериальной функции полезности в определенном виде.

Приведем без доказательств основную теорему многокритериальной теории полезности, на которой основаны практические методы оценки альтернатив.

Если условия независимости по полезности и независимости по предпочтению выполнены, то функция полезности является аддитивной

либо мультипликативной

где U, U_i — функции полезности, изменяющиеся от 0 до 1; w_i - коэффициенты важности (веса) критериев, причем 0< W_i<1; коэффициент k > 1. Таким образом, многокритериальную функцию полезности можно определить, если известны значения коэффициентов w_i, k, а также однокритериальные функции полезности U_i(x).

Полученный теоретический результат является основой метода, неоднократно использованного для решения практических задач. Обсудим приведенные выше этапы применения этого метода, используя в качестве примера задачу выбора площадки для строительства аэропорта

Построение однокритериальных функций полезности

Выше был приведен перечень критериев для оценки вариантов постройки аэропорта. Предположим, что после рассмотрения вариантов разброс оценок по критериям может быть представлен табл. 2.

Таблица 2. Разброс оценок вариантов постройки аэропорта

Критерий

Наихудшее

значение

Наилучшее

значение

(С₁) Стоимость постройки аэропорта

$ 200 млн

$ 100 млн

(С₂) Время поездки от центра города

90 мин.

40 мин.

(Сз) Количество людей, подвергающихся шумовым воздействиям

50 тыс.

5 тыс.

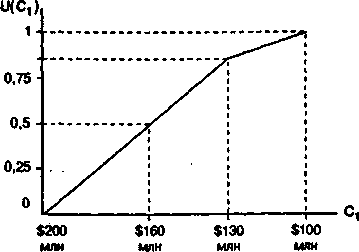
Зная диапазон изменения оценок по каждому из критериев, построим функцию, определяющую полезность для ЛПР каждой оценки из этого диапазона. Максимальное значение этой функции положим равным единице, а минимальное - нулю.

На рис.1 приведен пример построения функции полезности ЛПР для критерия «Стоимость постройки аэропорта».

Первоначально известны две точки функции полезности: U($100 млн)=1, U($200 млн)=0. Для нахождения промежуточных точек используются типовые лотереи (см. лекцию 2). В лотерее 1 на рис. 2 (слева) перед ЛПР ставится следующая задача: «Определите эквивалент определенности для лотереи, имеющей с равными вероятностями (р=0,5) минимальную и максимальную стоимости постройки». ЛПР предъявляют ряд значений (например, $120 млн, $130 млн и т.д.) и спрашивают: выше или ниже данного значения находится, по его мнению, эквивалент определенности. Предположим, что ЛПР остановился на значении $160 млн.

Рис. 1. Функция полезности для критерия С₁   «Стоимость постройки аэропорта»

Рис 4.2. Типовые лотереи, используемые при построении функции полезности по одному критерию

Тогда делается вывод, что U=0,5 соответствует $160 млн. Аналогично определяются другие значения функции полезности. Так, правая лотерея на рис.2 позволяет определить точку U($130 млн) = 0,85. Идентичным образом строятся функции полезности для каждого из критериев.

Проверка условий независимости

Для определения общей функции полезности необходимо проверить условия независимости по полезности и независимости по предпочтению. Проверку условия независимости по полезности можно совместить с предыдущим этапом построения однокритериальных функций полезности.

На рис. 3 приведена левая лотерея из рис. 2. Сначала лицу, принимающему решение, сообщается, что при нахождении эквивалента определенности он должен принять во внимание, что по остальным критериям имеются наилучшие значения (сверху справа на рис. 3). Затем перед ЛПР ставится та же задача, но уже при предположении, что по прочим критериям имеются наихудшие значения (снизу справа на рис. 3). Если эквивалент определенности в двух случаях одинаков, то делается вывод, что критерий не зависит по полезности от прочих критериев.

Проверка условий независимости

Для определения общей функции полезности необходимо проверить условия независимости по полезности и независимости по предпочтению. Проверку условия независимости по полезности можно совместить с предыдущим этапом построения однокритериальных функций полезности.

На рис. 3 приведена левая лотерея из рис. 2. Сначала лицу, принимающему решение, сообщается, что при нахождении эквивалента определенности он должен принять во внимание, что по остальным критериям имеются наилучшие значения (сверху справа на рис. 3). Затем перед ЛПР ставится та же задача, но уже при предположении, что по прочим критериям имеются наихудшие значения (снизу справа на рис. 3). Если эквивалент определенности в двух случаях одинаков, то делается вывод, что критерий не зависит по полезности от прочих критериев.

Рис.3. Проверка условия независимости по полезности

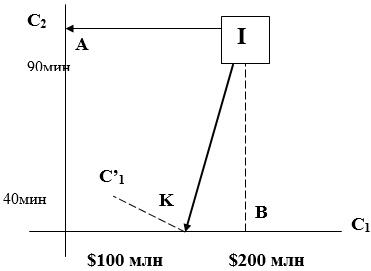
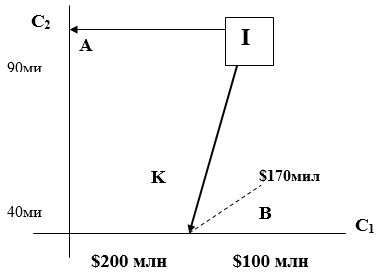
Отметим, что для полноты проверки условия независимости по полезности следует осуществлять эту проверку для всех лотерей (например, для лотереи 2 на рис. 2). Однако часто довольствуются приближенной проверкой — только для первой из лотерей, используемых при построении однокритериальных функций полезности.

При проверке условия независимости по предпочтению рассматривают плоскости, где по осям отложены значения двух критериев. Пример такой плоскости для критериев   С_{1 ,}С₂ приведен на рис. 4. Сначала предполагается, что по прочим критериям (в нашем случае — по критерию С₃) имеются наилучшие значения (С₃ = 5 тыс. человек).

Первоначально ЛПР должен определить свое предпочтение между альтернативами [(С₂)min; (С₁)mах] [(С₂)max; (С₁)min]]. В нашем случае ЛПР сравнивает площадки для постройки аэропорта с оценками (90, $100 млн) (40, $200 млн) - две крайние точки А и В на осях, при условии, что C₃=5 тыс. Предположим, что вариант А предпочтительнее. Это означает, что критерий стоимости более важен для ЛПР, чем критерий расстояния. Далее определяется такая точка на шкале критерия C₁, что варианты А и К одинаково предпочтительны для ЛПР. Иначе говоря, ищется такая стоимость строительства С₁, при которой одинаково предпочтительны варианты (90, $100 млн) и (40, С₁^* ). Затем точно такой же поиск точки безразличия осуществляется при С₃ = 50 тыс. Если результаты совпадают, то делается вывод, что пара критериев C₁, C₂ не зависит по предпочтению от третьего критерия.

Для полной проверки условия независимости по предпочтениям следует рассмотреть все лары критериев. Однако при приближенной проверке выбираются один или два наиболее существенных критерия и прочие рассматриваются только в паре с ними.

При проверке и первого, и второго условий независимости критерии, независимость от которых проверялась, имели крайние значения. Строго говоря, следовало бы рассмотреть и промежуточные значения, но обычно такая проверка считается достаточной.

Что делать, если какие-то из условий независимости не выполняются? Теория не дает единственного ответа на этот вопрос. Предлагается определить группу независимых критериев, найти функции полезности для подгрупп зависимых и независимых критериев и сформировать общую функцию полезности «по частям» либо переформулировать задачу. Можно сказать, что нарушение условий независимости существенно усложняет задачу. Поэтому в дальнейшем мы предполагаем, что условия независимости выполняются.

Определение весовых коэффициентов (коэффициентов важности) критериев

В MAUT существенно используются веса (коэффициенты важности) критериев. Считается, что ЛПР может найти коэффициенты — числа, которые определяют важность критериев. Отношения между весами критериев устанавливаются поиском точек безразличия на плоскостях двух критериев. В отличие от проверки условий независимости по предпочтению по осям упорядочиваются значения критериев от худших к лучшим.

На рис. 5 показана плоскость критериев С₁, С₂. Альтернативы А и К находятся в отношении безразличия, которое определяется так же, как и при проверке условия независимости по предпочтению (см. рис. 4).

Рис. 5. Определение отношения между весами критериев С₁и С₂



В точке равновесия полезности альтернатив равны, что позволяет записать U($200 млн, 40 мин.) =U($170 млн, 90 мин.). Это означает, что критерий стоимости важнее для ЛПР: W₁>W₂.

Используя полученные ранее однокритериальные функции полезности (рис. 2), находим W₂ = 0,4W₁. Аналогичным образом определяется соотношение между весами критериев С₁ и Сз. Пусть Wз = W₁, U($150 млн) = 0,6w₁. Итак, мы выразили веса всех критериев через вес наиболее важного из них и упорядочили критерии по важности : w₁>w₃>w₂.

Для нахождения численного значения веса критерия С₁ (и, следовательно, всех критериев) ЛПР предлагается сравнить две стратегии, представленные на рис. 6, и определить вероятность р, при которой обе стратегии равноценны. Первая стратегия - это альтернатива, имеющая лучшую оценку по первому критерию и худшую — по двум другим. Вторая стратегия — это лотерея, дающая с вероятностью р альтернативу со всеми лучшими оценками и с вероятностью (1—р) — альтернативу со всеми худшими оценками.

Предположим, что такое р найдено. Тогда U(А) = U(В), или w₁ = р. Пусть w₁ = 0,55. Тогда w₂ = 0,22; w_з = 0,33.





с. 6. Определение коэффициента W

Определение полезности альтернатив

После нахождения весов критериев и построения однокритериальных функций полезности мы имеем всю необходимую информацию. В соответствии с теоретическими результатами остается установить вид функции полезности. В нашем примере сумма коэффициентов важности критериев

Считая полученное значение достаточно близким к единице, выбираем аддитивную форму представления функции полезности:

Зная оценки альтернатив (вариантов площадок), можем подставить их в эту формулу, определить полезность каждой альтернативы, сравнить полезности и выбрать альтернативу с наибольшей полезностью.

Пусть заданы четыре альтернативы со следующими оценками:

А ($ 180 млн, 70 мин., 10 тыс.);

В ($ 170 млн, 40 мин., 15 тыс.);

С ($ 160 млн, 55 мин., 20 тыс.);

D ($ 150 млн, 50 мин., 25 тыс.).

Подставляя в формулы для вычисления полезности альтернатив значения полезностей оценок и веса критериев, получаем:

Итак, альтернатива D — лучшая.

                  4.Метод SMART - простой метод многокритериальной оценки

Подход, основанный на теории многокритериальной полезности, требует достаточно много усилий при практическом применении. В детальном примере из книги приведено множество вопросов к ЛПР, ответы ЛПР в многочасовом диалоге с консультантом. Как реакцию на сложность методов, основанных на MAUT, можно оценить появление ряда эвристических методов, не имеющих строго математического обоснования, но использующих простые процедуры получения информации в ее агрегации в общую оценку альтернативы.

Одним из наиболее известных методов такого типа является метод SMART, предложенный В. Эдвардсом. Метод можно представить как совокупность следующих этапов:

1.   Упорядочить критерии по важности.

2.   Присвоить   наиболее   важному   критерию   оценку   100
баллов. Исходя из попарного отношения критериев по важности, дать в баллах оценку каждому из критериев.

3. Сложить полученные баллы. Произвести нормировку весов критериев, разделив присвоенные баллы на сумму весов.

4. Измерить значение каждой альтернативы по каждому из
критериев по шкале от 0 до 100 баллов.

5. Определить общую оценку каждой альтернативы, используя формулу взвешенной суммы баллов.

6.    Выбрать как лучшую альтернативу, имеющую наибольшую общую оценку.

7.    Произвести, оценку чувствительности результата к изменениям весов.

По признанию автора, метод SMART не учитывает возможную зависимость измерений и неаддитивность при определении общей ценности альтернативы. Однако, по его мнению, метод прост и надежен при практических применениях, что более существенно. Проверка чувствительности к изменениям весов позволяет учесть влияние неточностей при измерениях и возможной зависимости между критериями.

5.Первый эвристический метод

Существует много вариантов метода SMART, а также много других эвристических (не имеющих строгого обоснования) методов принятия решений. Весьма вероятно, что первый из них был предложен в письме знаменитого американского ученого и политического деятеля Б. Франклина к своему другу Д. Пристли, который задал ему вопрос о том, как следует принимать решения. Заметим, что это письмо было послано 19 сентября 1772 г. Цитируем его по одной из многочисленных ссылок.

«Когда встречаются трудные случаи, то они трудны, главным образом, потому, что при их рассмотрении все доводы «за» и «против» не присутствуют в уме одновременно; иногда присутствует одна часть, в другое время - иная, причем первая исчезает из вида. Следовательно, различные цели или склонности по очереди берут «верх» и появляется неопределенность, которая озадачивает нас.

Мой путь преодоления этого состоит в том, чтобы разделить половину листа бумаги линией на два столбца; в одном писать доводы «за», а в другом - «против». Затем, после размышления в течение трех или четырех дней, я излагаю под другими заголовками короткие намеки на разные побуждения, которые в различные моменты времени приходят мне в голову и говорят «за» или «против» варианта действий.

Когда я имею все это вместе в поле зрения, я пытаюсь оценить их соответствующие веса; если я найду два, каждый на другой стороне, которые кажутся равными, я их вычеркиваю. Если я нахожу довод «за», равный двум доводам «против», я вычеркиваю все три. Если я считаю, что некоторые два довода «за» равны трем доводам «против», я вычеркиваю все пять; продолжая таким образом я нахожу со временем, где находится баланс; и если через день или два дальнейших размышлений ничего нового не появляется на каждой стороне, я прихожу к соответствующей определенности».

1.     Веса критериев

Понятие коэффициентов важности (весов) критериев применяется как в строгих методах, основанных на MAUT, так и в эвристических методах. Формализация этого понятия была предложена В.В. Подиновским.

Обозначим векторную оценку альтернативы А_i как Х_i=(х₁ⁱ...х_Nⁱ). Обозначим через векторную оценку, полученную из x_i перестановкой ее компонентов и . Предположим, что все критерии — числовые и большие значения лучше меньших.

Определение 1. Критерии С_i и С_j - равноважные, если каждые две векторные оценки x_i и одинаковы по предпочтительности.

Определение 2. Утверждение «критерий С_j важнее критерия С_k» означает, что векторная оценка x_i в которой   , предпочтительнее оценки .

Таким образом, упорядочение критериев по важности предполагает, что есть какая-то общая для всех критериев шкала с одинаковой интерпретацией оценок.

На основе формальных определений можно получить различные правила сравнения альтернатив. Так, можно упорядочить компоненты двух векторов x_i  и x_j по невозрастанию и затем почленно сравнить, определяя случаи эквивалентности и доминирования по Э-П.

Наряду с приведенными выше определениями вводятся понятия степени превосходства критериев (один критерий в t раз важнее другого) и количественные веса критериев.

7. Как люди назначают веса критериев

Как в методах, имеющих аксиоматическое обоснование, так и в эвристических методах информация, необходимая для определения коэффициентов важности критериев может быть получена только от ЛПР. Существуют различные способы определения весов критериев. Приведем наиболее известные из них.

1. Метод отношений, который был представлен выше как
этап в методе SMART. ЛПР ранжирует критерии по важности,
вес наиболее важного назначается как 100 баллов (либо вес
наименее важного назначается как 10 баллов), а веса других
критериев определяются из отношений критериев по важности.

2. Метод наибольших отклонений (swing). Предполагаются худшие оценки по всем критериям, а затем ЛПР просят
оценить, по какому критерию изменение от худшей оценки до
лучшей оценки наиболее важно. Затем находится второй по
важности критерий и т.д. Изменению наиболее важного критерия (swing) присваивается 100 баллов. ЛПР просят определить
в баллах значения изменений от худших до лучших оценок по
остальным критериям.

3.    Метод компенсации был представлен выше как этап метода, основанного на MAUT. При методе компенсаций сравниваются две альтернативы, различающиеся оценками только по
двум критериям, и определяются точки безразличия на плоскостях двух критериев.

4. Метод определения цены критериев является вариантом
метода наибольших отклонений. ЛПР должен определить, какую сумму денег он готов заплатить за переход от худшего к
лучшему значению по каждому из критериев. При этом как базовый берется критерий стоимости.

5.    Метод взвешенной полезности также был представлен в
виде последнего этапа метода, основанного на MAUT. При этом
методе ЛПР назначает вероятность р, при которой он безразличен при выборе между альтернативой, имеющей лучшую оценку по i-му критерию и худшую — по остальным, и лотереей, дающей с вероятностью р альтернативу со всеми лучшими оценками и с вероятностью (1—р) — альтернативу со всеми худшими оценками.

Наряду с различными способами определения весов принято рассматривать две различные структуры объединения критериев: иерархическую (критерии более общего характера разделяются на частные) и неиерархическую.

В настоящее время известны результаты многих психологических экспериментов, в которых сравнивались различные способы назначения весов критериев. Общий результат неутешителен: эти способы дают различные результаты, которые могут привести к различиям в упорядочении альтернатив. Иначе говоря, человеческие ошибки при определении весов критериев тем или иным способом могут привести к различным результатам при принятии решений.

8. Практическое применение

Методы, основанные на MAUT, а также упрощенные эвристические методы применялись для решения большого количества практических задач. Примером одной из таких задач является выбор способа утилизации оружейного плутония. После работы группы экспертов было принято решение включить в список 13 альтернатив, разбитых на три группы: непосредственное хранение (две альтернативы); спекание в стеклообразный материал (шесть альтернатив); сжигание в различного типа реакторах (пять альтернатив).

Для оценки альтернатив использовались четыре критерия: стоимость (капиталовложения); стоимость жизненного цикла; время начала утилизации и количество лет для выполнения утилизации.

Для каждого из критериев эксперты построили однокритериальные функции полезности и нашли полезности для каждой из альтернатив. Эксперты определили также веса критериев. Для агрегации оценок использовалась формула взвешенной суммы оценок критериев. Для проверки чувствительности результатов анализа к возможным неточностям в весах критериев было проведено статистическое моделирование, позволившее получить окончательное ранжирование альтернатив.

Выводы

1.Существуют две группы задач принятия решений. В задачах
первой группы осуществляется анализ заданных альтернатив.
В задачах второй группы находится решающее правило, позволяющее оценить любые альтернативы. Разработаны многокритериальные методы решения задач, принадлежащих к первой и второй группам.

2.Многокритериальная теория полезности (MAUT) представляет
собой дальнейшее развитие теории полезности. Методы MAUT
имеют аксиоматическое обоснование: вводятся аксиомы и доказывается существование функции полезности в той или иной
форме. Особо важную роль играют аксиомы (условия) независимости, определяющие, что отношения между частью критериальных оценок альтернатив не зависят от фиксированных значений по другим критериям.

3.Методы MAUT позволяют определить полезность каждой из альтернатив. Наиболее целесообразно применение этих методов
для задач первой группы с большим числом альтернатив.

4.Имеется большое число эвристических методов, использующих
аддитивную формулу взвешенной суммы оценок альтернатив
без исследования вопросов о зависимости критериев и без строгого обоснования вида функции полезности. Одним из известных
методов такого типа является метод SMARТ.

5.Существуют различные подходы к выявлению предпочтений
ЛПР по отношению к относительной важности критериев. Психологические исследования показывают, что различные методы
выявления весов критериев приводят к различным результатам.

Сайт создан по технологии «Конструктор сайтов e-Publish»