|
| |||||||||||||||||
|
Тема 4. Аксиоматические теории рационального поведения.1.Рациональный выбор в экономике. 2. Аксиомы рационального поведения. 3. Деревья решений 4. Парадокс Алле 5. Нерациональное поведение. Эвристики. 6.Объяснения отклонений от рационального поведения 7. Теория проспектов.
1.Рациональный выбор в экономике.
Задача выбора является одной из центральных в экономике. Два основных действующих лица в экономике – покупатель и производитель – постоянно вовлечены в процесс выбора. Потребитель решает, что покупать и за какую цену. Производитель решает, во что вкладывать капитал, какие товары следует производить и др. Основное допущение экономической теории состоит в том, что человек делает рациональный выбор. Рациональный выбор означает предположение, что решение человека является результатом упорядоченного процесса мышления. Для определения этого понятия в строго математической форме выводятся аксиомы рационального поведения. При условии, что аксиомы справедливы, доказывается, что существует некая функция, устанавливающая человеческий выбор – функция полезности. Под полезностью будем понимать величину, которая в процессе выбора максимизирует личность с рациональным экономическим мышлением. Иначе говоря – полезность – это воображаемая мера психологической и потребительской ценности различных благ. С содержательной точки зрения делается предположение, что человек оценивает различные альтернативы и выбирает из них ту, полезность которой больше. ЗПР с рассмотрением полезностей были первыми, которые привлекли внимание исследователей. Постановка таких задач заключается в следующем: человек выбирает какие-то действия, где на получаемый результат (исход) действия влияют случайные события, неподвластные человеку, но, имея некоторые знания о вероятностях этих событий, человек может рассчитывать наиболее выгодную совокупность и очерёдность своих действий. Человек, который следует аксиомам рационального выбора, называется в экономике рациональным человеком.
2. Аксиомы рационального поведения.
Через x, у, z различные исходы (результаты) процесса выбора, а через p, q – вероятности тех или иных исходов. Лотереей называется игра с двумя исходами: исходом x, получаемым с вероятностью p, и исходом y, получаемым с вероятностью (1-p) ( рис.1)
Ожидаемая (или средняя цена) лотереи определяется по формуле p x+(1-p)y. Приведем аксиомы рационального выбора: Аксиома 1. Пусть P означает строгое предпочтение (похожие на > в математике); R – не строгое предпочтение (похожее на >=); I – безразличие (похожее на =). Аксиома 1. требует выполнения 2-х условий: 1) связности: либо x R y, либо y R x, либо и то и другое вместе; 2) транзитивности: из x R y и y R x следует x R z Аксиома 2. Если x I y, то (x, p, z) I (y, p, z) (через (x, p, y) обозначается лотерея на рис.1). Аксиома 3. Если x P y, то x P (x, p, y) P y Аксиома 4. Если x P y P z , то существует вероятность p, такая, что yI (x, p, z). Аксиомы, приведенные выше достаточно просты для понимания. В предположении, что они выполняются, имеет место теорема, которая гласит, что существует числовая функция полезности U, определенная на множестве исходов и такая, что: 1) x R y тогда и только тогда, когда U (x) >= U(y) 2) U (x, p, y) = p U(x) + (1-p) U(y)
3. Деревья решений
Для представления своих возможных действий и для нахождения последовательности правильных решений используется дерево решений. Рассмотрим пример задачи с вазами. Экспериментатор случайно выбирает вазу из множества ваз, содержащего 700 ваз 1-го типа и 300 ваз 2-го типа. Если перед испытуемым находится ваза 1-го типа и он угадает это, то он получит выигрыш 350 у.е., если не угадает, то его проигрыш составит 50 у.е. Если перед ним ваза 2-го типа и он это угадает, то получит выигрыш 500 у.е., если не угадает, его проигрыш составит 100 у.е. Испытуемый может предпринять одно из следующих действий: d1 – сказать, что ваза 1-го типа; d2 – сказать, что ваза 2-го типа. Условия задачи можно представить в таблице 1.
Таблица 1.
Какое действие предпринять человеку? На основе теории полезности для этого необходимо оценить среднюю (ожидаемую) полезность каждого из действий и выбрать действие с максимальной ожидаемой полезностью. Оценка полезности дает: U (d1) = 0.7 *350 – 0.3 * 50 = 230 y.e. U (d2) = 0.3 *500 – 0.7 * 100 = 80 y.e. Следовательно, разумный человек выберет действие d1, а не действие d2. Отсюда следует общий рецепт действий для рационального человека: для каждого действия определить ожидаемую полезность и выбрать действие с наибольшей полезностью. Таблица 1. может быть представлена в виде дерева решений . Дерево решений удобно использовать для представления своих возможных действий и для нахождения последовательности правильных решений, ведущих к максимальной ожидаемой полезности.
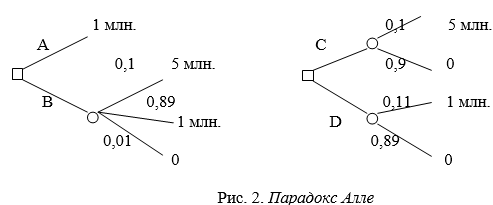
4. Парадокс Алле Рассмотрим две лотереи, представленные на рис. 2.
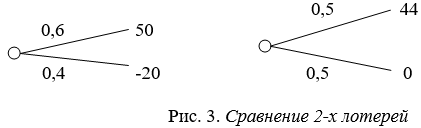
Обозначим: U ( 5млн )=1; U(1млн ) =U; U (0) = 0. В левой лотереи есть выбор между действиями А (получить 1 млн.) и В (согласиться на лотерею). В экспериментах подавляющее большинство людей предпочитает А. Откуда следует U > 0.1*1 + 0.89*U + 0.01*O или U > 10/11 В правой лотерее есть выбор между действиями С и D (две лотереи). Подавляющее большинство людей предпочитает действие С (почти та же вероятность проиграть, но выигрыш больше). Тогда 0.1*1 + 0.9*O > 0.11*U + 0.89*O т.е. U < 10/11. Совершая такой выбор, люди действуют не в соответствии с функцией полезности. Полученный парадокс носит название парадокса Алле. Рассмотрим ещё пример. Две лотереи, показанные на рис.3 имеют одинаковые средние цены.
0.6*50 + 0.4* (-20) = 22 0.5*44 + 0.5 * 0 = 22. Однако предъявление различным группам лотерей показало, что люди предпочитают правую лотерею, где при той же средней цене риск проигрыша исключен. Эти и другие примеры говорят о нерациональном поведении людей в задачах принятия решений.
5. Нерациональное поведение. Эвристики.
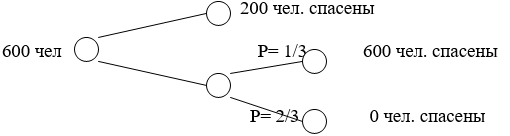
Один из наиболее известных примеров нерационального поведения людей – «дилемма генерала». Генерал потерпел поражение в войне и хочет вывести свои войска (600 чел.) с территории противника. У него есть две возможные дороги с возможными потерями при выборе каждой из них. Данные о дорогах и возможных потерях представлены на рис. 4.
Рис. 4. Дилемма генерала
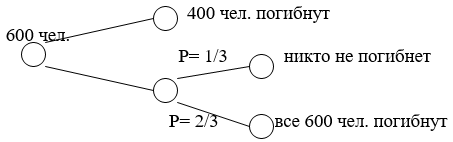
Большинство людей рассматривающих дилемму выбирают первую дорогу, стараясь избежать лотереи, когда в одном из исходов погибает весь личный состав соединения. Но эта же дилемма была представлена используемым в ином виде (рис. 5.)
Рис. 5. Иное представление дилеммы генерала
Теперь уже большинство испытуемых выбирает вторую дорогу, т. к. на ней с вероятностью р = 1/3 можно спасти все соединение. Легко видеть, что лотереи на рис. 4 и 5 эквивалентны. Эти и другие примеры демонстрируют отклонение поведения людей от рационального поведения, определяют эвристики, которые используются при принятии решений. Перечислим наиболее известные эвристики.
1. Суждение по представительности. Люди часто судят о вероятности того, что объект А принадлежит к классу В только по похожести А на типовой объект класса В. Они почти не учитывают априорные вероятности, влияющие на эту принадлежность. 2. Суждение по встречаемости. Люди часто определяют вероятности событий по тому, как часто они сами сталкивались с этими событиями и насколько важными для них были эти встречи. 3. Суждение по точке отсчета. Если при определении вероятностей используется начальная информация как точка отсчета, то она существенно влияет на результат. 4. Сверхдоверие. Людям свойственно чрезмерно доверять своим суждениям, особенно в случаях, когда они выносят суждения о прошлых событиях. 5. Стремление к исключению риска. Люди стремятся исключить альтернативы связанные с риском.
6.Объяснения отклонений от рационального поведения.
Признание нерациональности человеческого поведения привело к поиску его причин, основными из которых являются: -Недостаток информации у ЛПР в процессе выбора -Недостаточный опыт ЛПР -Стремление ЛПР найти решение, оптимальное с точки зрения совокупности критериев (целей), строго упорядоченных по важности, но он не может его найти -Различие между объективно требуемым временем для реализации планов и субъективным горизонтом планирования ЛПР. При анализе решений экономического выбора знание и учет нерационального человеческого поведения весьма важно. Существует и такое мнение, что рынок приучает к рациональности, что значительные отклонения от рациональности могут привести к разорению ЛПР. Стремление учесть реальное поведение людей и приблизить теорию к жизни привело к появлению теории проспектов.
7. Теория проспектов.
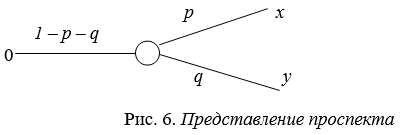
Теория проспектов была разработана для того, чтобы учесть реальные черты человеческого поведения в задачах с субъективными вероятностными оценками. Теория проспектов позволяет учесть три поведенческих эффекта: 1. эффект определенности, т. е. тенденцию придавать больший вес детерминированным исходам 2. эффект отражения, т. е. тенденцию к изменению предпочтений при переходе от выигрышей к потерям 3. эффект изоляции, т. е. тенденцию к упрощению выбора путем исключения общих компонентов вариантов решений. Рассмотрим игру (x, p, y, q), где исход Х осуществляется с вероятностью p, исход Y – с вероятностью q, а нулевой исход – с вероятностью (1 – p – q), рис. 6. В теории проспектов игра, представленная на рис. 6, называется проспектом. Оценивается ценность (а неожидаемая полезность) этой игры по следующей формуле: V = V(x)* П(р) + V(y)* П(q), где V(x), V(y) – ценность исходов x, y соответственно, V(0) = 0 и П(р), П(q) – вес (важность) вероятностей p, q соответственно.
Отметим некоторые отличия теории проспектов от теории полезности: -Использование функции от вероятностей вместо вероятностей -Полезность определялась как прибавление к первоначальному благосостоянию человека. Ценность же отсчитывается от любого уровня, принятого за - исходный. -Для учета поведенческих аспектов предполагается, что функция V(x) ценности – выпуклая для выигрышей и вогнутая – для потерь (Рис. 7.) Рис. 7. Функция ценности V(x).
Функция вероятности П(р) построена специальным образом для учета поведенческих аспектов. Прежде всего П(р) не подчиняется всем законам теории вероятностей. Отметим следующие свойства П(р): 1) П(0) = 0 2) П(р) + П(1 – р) < 1 3) При малых вероятностях П(р)>р 4) Отношение П(р) / П(q) ближе к единице при малых вероятностях, чем при больших. 5) П(р) плохо определена у крайних значений. Покажем, что применение новой теории проспектов позволяет избежать парадокса Алле. Из левой лотереи следует U > П(0,1) / 1 – П(0,89) Из правой лотереи следует П(0,1) / П(0,11) > U Или же П(0,1) / П(0,11) > U > П(0,1) / 1- П(0,89) Так как из свойств функции П(р) вытекает возможность выполнения неравенства 1 – П(0,89) > П(0,11) и 1 > П(0,89) + П(0,11), то в теории проспектов парадокс Алле уже не имеет места. | ||||||||||||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | |||||||||||||||||