|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Лекция 4 Логические основы функционирования вычислительных машин
1. Комбинационные схемы Обработка входной информации Х в выходную Y в любых схемах ВМ обеспечивается преобразователями или цифровыми автоматами двух видов: комбинационными схемами и схемами с памятью. Комбинационные схемы (КС) — это схемы, у которых выходные сигналы Y = (у1, у2,..., уm) в любой момент дискретного времени однозначно определяются совокупностью входных сигналов Х= (х1 х2,..., хп), поступающих в тот же момент времени t. Реализуемый в КС способ обработки информации называется комбинационным потому, что результат обработки зависит только от комбинации входных сигналов и формируется сразу же при поступлении входных сигналов. Поэтому одним из достоинств, комбинационных схем является их высокое быстродействие. Преобразование информации однозначно описывается логическими функциями вида Y = f(X). Логические функции и соответствующие им комбинационные схемы подразделяют на регулярные и нерегулярные структуры. Регулярные структуры предполагают построение схемы таким образом, что каждый из ее выходов строится по аналогии с предыдущими. В нерегулярных структурах такая аналогия отсутствует. В практике проектирования ВМ накоплен огромный опыт по синтезу различных схем. Многие регулярные структуры положены в основу построения отдельных ИС малой и средней степени интеграции или отдельных функциональных частей БИС и СБИС. Из регулярных комбинационных схем наиболее распространены дешифраторы, шифраторы, схемы сравнения, комбинационные сумматоры, коммутаторы и др. Рассмотрим принципы построения подобных регулярных структур. Дешифраторы (ДШ) — это комбинационные схемы с п входами и т=2n выходами. Единичный сигнал, формирующийся на одном из т выходов, однозначно соответствует комбинации входных сигналов. Например, разработка структуры ДШ для n=3 позволяет получить следующую таблицу истинности (табл. 1.3) и логические зависимости. Дешифраторы широко используются в ВМ для выбора информации по определенному адресу, для расшифровки кода операции и др. Логические зависимости дешифратора:
Таблица 1.3 Таблица истинности шифратора (входы и выходы указаны в верхней части таблицы) и дешифратора (входы и выходы в нижней части таблицы)
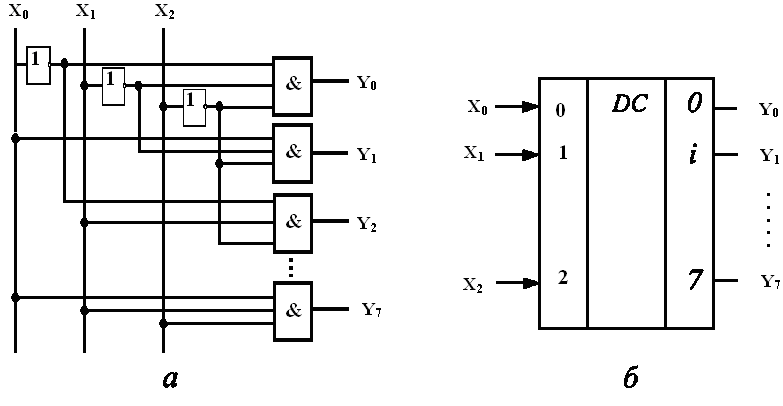
На рис. 4. представлены структурная схема ДШ, построенная в базисе (И, НЕ), и условное ее обозначение на принципиальных электрических схемах ВМ. Кружочки у линий, выходящих из логических элементов, указывают на инверсию функций, реализуемых элементами.
Рис. 4. Структурная схема дешифратора (а) и обозначение дешифратора на принципиальных электрических схемах (б)
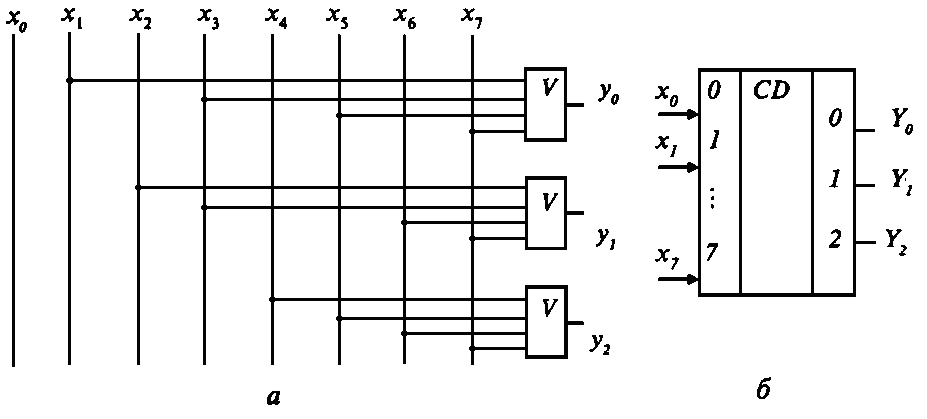
Рис. 5. Структурная схема шифратора (а) и обозначение шифратора на принципиальных электрических схемах (б) Шифратор (ШР) решает задачу, обратную схемам ДШ, т.е. по номеру входного сигнала формирует однозначную комбинацию выходных сигналов. Пример построения ШР иллюстрируется таблицей истинности (табл. 1.3) и схемами на рис. 5. Состояния входов ШР в табл. 1.3 содержат только по одному единичному элементу. Другие произвольные комбинации входов недопустимы. Рассмотрим логическое устройство, называемое сумматором. Его назначение состоит в нахождении суммы двух двоичных чисел. Этот узел интересен для нас тем, что он лежит в основе АЛУ ЦП и иллюстрирует некоторые принципы выполнения вычислительных операций в компьютере. Для простоты начнем с изучения логической структуры простейшего возможно устройства, являющегося звеном сумматора. Это устройство – полусумматор. Он реализует сложение двух одноразрядных двоичных чисел, которые обозначим А и В в результате получается, вообще говоря, двухразрядное двоичное число. Его младшую цифру обозначим S, а старшую, которая при сложении многоразрядных чисел будет перенесена в старший разряд, через Со (от английских слов «Carry out» – «выходной перенос»). Для лучшего понимания происходящего вспомните Правило типа «ноль пишем, один в уме». Обе цифры можно получить по следующим логическим формулам (черта над символом обозначает операцию NOT, знак ^ – конъюнкцию, знак v – дизъюнкцию):
Таблица 1.4 Таблица истинности для полусумматора
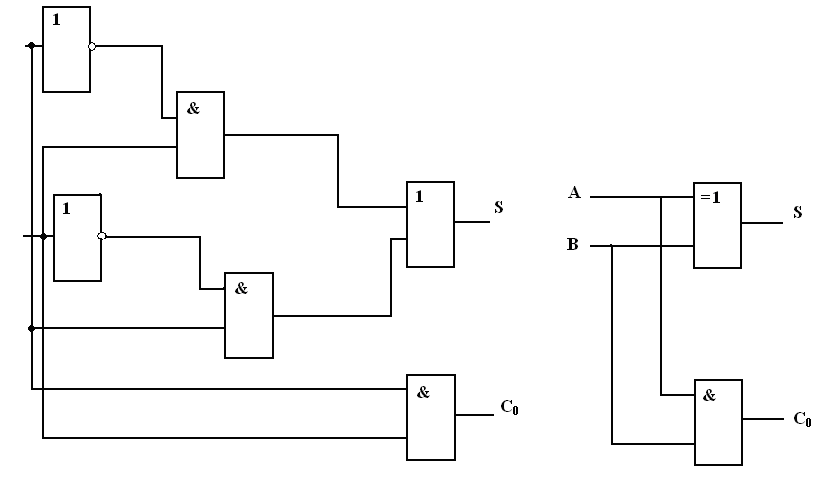
Это легко проверить перебором всех четырех возможных случаев сочетания значении А и В, пользуясь табл. 1.4 и табл. 1.5. Мысленно объединим в табл. 1.4 столбцы А, В и Со. Полученная таблица напоминает базовый логический элемент И. Аналогично, сравнив первые три столбца А, В и S с имеющимися в предыдущем разделе таблицами истинности для распространенных логических элементов, обнаружим подходящий для наших целей элемент «исключающее ИЛИ». Таким образом, для реализации полусумматора достаточно соединить параллельно входы двух логических элементов (рис. 6). Таблица 1.5 Таблица истинности для полного сумматора
Ниже приведены два варианта логической схемы полусумматора: с использованием лишь базовых логических элементов и с использованием логического элемента «исключающее ИЛИ». Видно, что вторая схема существенно проще.
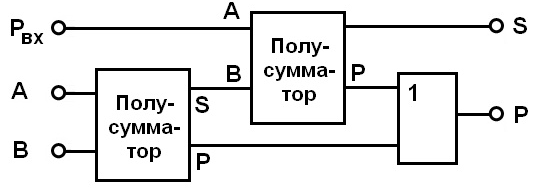
Рис 6. Логическая схема полусумматора (два варианта) Полный одноразрядный сумматор «умеет» при сложении двух цифр учитывать возможное наличие единицы, переносимой из старшего разряда (той, которая при обычном сложении столбиком остается «в уме»). Обозначим этот «бит переноса» через Ci (от английского «Carry in» – «входной перенос»). При построении схемы сумматор удобно представить в виде двух полусумматоров, из которых первый суммирует разряды А и В, а второй к полученному результату прибавляет бит переноса Ci.
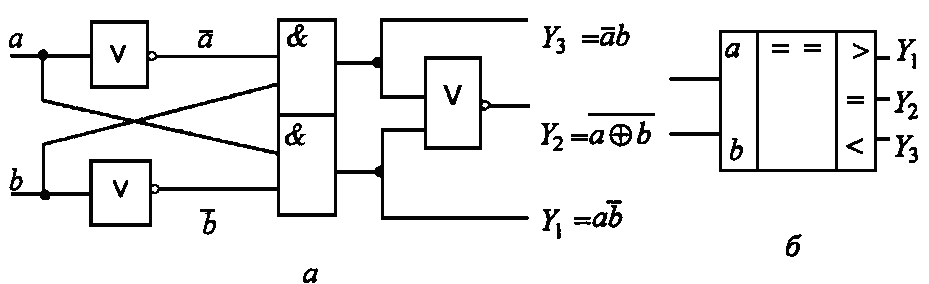
Рис7. Сумматор, составленный из двух полусумматоров Заметим, что для суммирования младших разрядов чисел полусумматора уже достаточно, так как в этом случае отсутствует сигнал входного переноса. Соединив два полусумматора как показано на рис. 7, получим полный сумматор, способный осуществить сложение двух двоичных разрядов с учетом возможности переноса. Перейти к многоразрядным числам можно путем последовательного соединения соответствующего количества сумматоров. Схемы сравнения, или компаратор, обычно строятся как поразрядные. Они широко используются неавтономно, и в составе более сложных схем, например, при построении сумматоров. Таблица истинности (табл. 1.6) отражает логику работы i-го разряда схемы сравнения при сравнении двух векторов — А и В. На рис. 9. показана структурная схема компаратора. Таблица 1.6 Таблица истинности компаратора
На схеме 1.13. У1 и У3 соответствующие сигналам «больше» и «меньше».
Рис. 9. Структурная схема компаратора (а) и обозначение компаратора на принципиальных электрических схемах (б) 2. Схемы с памятью Более сложным преобразователем информации являются схемы с памятью. Наличие памяти в схеме позволяет запоминать промежуточные состояния обработки и учитывать их значения в дальнейших преобразованиях. Выходные сигналы Y= (y1,y2,…,yn) в схемах данного типа формируются не только по совокупности входных сигналов Х = (x1,x2,…,xn), но и по совокупности состояний схем памяти Q = (q1,q2,…,qk). При этом различают текущий дискретный момент времени t и последующий (t + 1) момент времени. Передача значения Q между моментами времени t и (t+1) осуществляется обычно с применением двухступенчатой памяти и синхронизирующих импульсов (СИ). В качестве простейшего запоминающего элемента в современных ЭВМ используют триггеры. Перейдем к описанию работы триггера. Соответствующая его работе таблица истинности (табл. 1. 7) приведена ниже. Таблица 1. 7 Таблица истинности RS-триггера
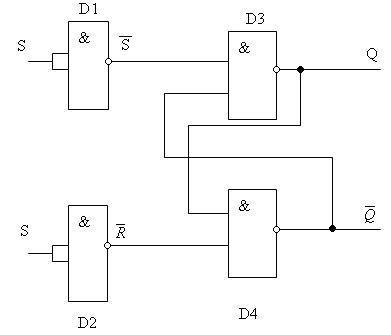
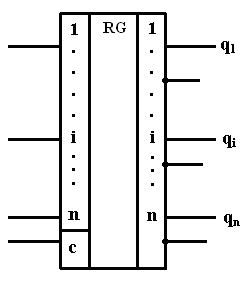
Рис. 10. Логическая схема триггера Как видно из рис. 10, простейший вариант триггера собирается из четырех логических элементов И-НЕ, причем два из них играют вспомогательную роль Триггер имеет два входа, обозначенные на схеме R и S, а также два выхода, помеченные буквой Q – прямой и инверсный (черта над Q у инверсного выхода означает отрицание). Триггер устроен таким образом, что на прямом и инверсном выходах сигналы всегда противоположны. Как работает триггер? Пусть на входе R установлена 1, а на S – 0. Логические элементы D1 и D2 инвертируют эти сигналы, т. е. меняют их значения на противоположные. В результате на вход элемента D3 поступает 1, а на D4 – 0. Поскольку на одном из входов D4 есть 0, независимо от состояния другого входа на его выходе (он же является инверсным выходом триггера!) обязательно установится 1. Эта единица передается на вход элемента D3 и в сочетании с 1 на другом входе порождает на выходе D3 логический 0. Итак, при R=1 и S=0 на прямом выходе триггера устанавливается 0, а на инверсном – 1. Обозначение состояния триггера по договоренности связывается с прямым выходом. Тогда при описанной выше комбинации входных сигналов результирующее состояние можно условно назвать нулевым: говорят, что триггер «устанавливается 0» или «сбрасывается». Сброс по-английски называется «Reset», отсюда вход, появление сигнала на котором приводит к сбросу триггера, обычно обозначают буквой R. Проведите аналогичные рассуждения для «симметричного» случая R = 0 и S = 1. Вы увидите, что на прямом выходе получится логическая 1, а на инверсном – 0. Триггер перейдет в единичное состояние – «установится» (установка по-английски – «Set»). Теперь рассмотрим наиболее распространенную и интересную ситуацию R = 0 и с = 0 – входных сигналов нет. Тогда на входы элементов D3 и D4, связанные с R и с – будет подана 1 и их выходной сигнал будет зависеть от сигналов на противоположных входах. Нетрудно убедится, что такое состояние будет устойчивым. Пусть, например, на прямом выходе 1. Тогда наличие единиц на обоих входах элемента D4 «подтверждает» нулевой сигнал на его выходе. В свою очередь, наличие 0 на инверсном выходе передается на D3 и поддерживает его выходное единичное состояние. Аналогично доказывается устойчивость картины и для противоположного состояния триггера, когда Q = 0. Таким образом, при отсутствии входных сигналов триггер сохраняет свое «предыдущее» состояние. Иными словами, если на вход R подать 1, а затем убрать, триггер установится в нулевое состояние и будет его сохранять, пока не поступит сигнал на другой вход S. В последнем случае он перебросится в единичное состояние, и после прекращения действия входного сигнала будет сохранять на прямом выходе 1. Мы видим, что триггер обладает замечательным свойством: после снятия входных сигналов он сохраняет свое состояние, а значит, может служить устройством для хранения одного бита информации. В заключение проанализируем последнюю комбинацию входных сигналов: R = 1 и S = 1. Нетрудно убедиться (проделайте необходимые рассуждения самостоятельно), что в этом случае на обоих выходах триггера установится 1! Такое состояние помимо своей логической абсурдности еще и является неустойчивым: после снятия входных сигналов триггер случайным образом перейдет в одно из своих устойчивых состояний. Вследствие этого, комбинация R = 1 и S = 1 никогда не используется на практике и является запрещенной. Мы рассмотрели простейший RS-триггер. Существуют и другие разновидности этого интересного и полезного устройства. Все они различаются не столько принципом работы, сколько входной логикой, усложняющей «поведение» триггера. Триггеры очень широко применяются в вычислительной технике. На их основе изготовляются всевозможные регистры для хранения и некоторых видов обработки (например, сдвига) двоичной информации, счетчики импульсов и даже интегральные микросхемы статического ОЗУ, не требующие для сохранения информации специальных процессов регенерации. Множество триггеров входят в состав любого микропроцессора. Триггер помнит только один двоичный разряд. Для хранения многоразрядных чисел триггеры объединяют в устройство, называемое регистром. Регистр — важнейший элемент ВМ, являющийся типовым блоком памяти малого объёма ОЗУ. Различают регистры общего и специального назначения. Регистры составляют основу архитектуры процессора. Среди обязательного набора регистров можно отметить следующие. Регистр данных — служит для временного хранения промежуточных результатов при выполнении операций. Регистр аккумулятор — регистр временного хранения, который используется в процессе вычислении (например, в нем формируется результат выполнения команды умножения). Регистр указатель стека — используется при операциях со стеком, т.е. такой структурой данных, которая работает по принципу: последним вошел — первым вышел, т.е. последнее записанное в нем значение извлекается из него первым. Пока отметим только, что стеки используются для организации подпрограмм. Индексные, указательные и базовые регистры используются для хранения и вычисления адресов операндов в памяти. Регистры-счетчики используются для организации циклических участков в программах. Регистры общего назначения, имеющиеся во многих ВМ, могут использоваться для любых целей. Точное назначение такого регистра определяет программист при написании программы. Они могут использоваться для временного хранения данных, в качестве аккумуляторов, а также в качестве индексных, базовых, указательных регистров. Количество регистров и связей между ними оказывает существенное влияние на сложность и стоимость процессора. Однако, с другой стороны, наличие большого количества регистров с богатым набором возможностей упрощает программирование и повышает гибкость программного обеспечения. Кроме перечисленных регистров в состав ЦП могут входить регистры специального назначения, внутренние системные регистры, не доступные программно и используемые во время внутренних пересылок информации при выполнении команд. Это так называемые индикаторы, флаги и пр. Условное обозначение регистра изображено на рис. 11.
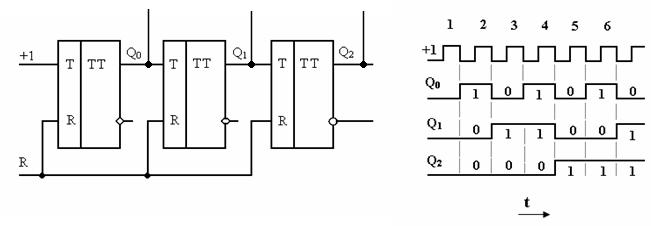
Рис. 11. Условное обозначение регистра. С (Clock — часы) — вход синхронизирующих тактовых импульсов Счётчиком называется функциональный узел, предназначенный для подсчета числа поступающих на его входы сигналов (обычно импульсов) и фиксации результата в виде многоразрядного двоичного числа. Количество разрядов (триггеров) в счётчике п определяет количество различных устойчивых состояний 2п такой триггерной системы. Последние называют коэффициентом перерасчёта Ксч. В основу построения любого счётчика положено свойство Т – триггера каждый раз изменять своё состояние при подаче очередного сигнала на счётный вход (рис.12.)
Рис. 12. Схема простейшего суммирующего двоичного счётчика и временные диаграммы, поясняющие его работу
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||