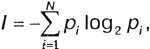Запись чисел с фиксированной точкой. При представлении в памяти компьютера чисел в естественной форме устанавливается фиксированная длина разрядной сетки. Точку (запятую) можно зафиксировать в начале, середине или конце разрядной сетки. При этом распределение разрядов между целой и дробной частями остается неизменным для любых чисел. В связи с этим существует другое название естественной формы представления чисел - с фиксированной точкой (запятой). В современных компьютерах эта форма используется для представления целых чисел.
Обычно целые числа занимают в памяти компьютеров один, два или четыре байта. Один, как правило, старший бит отводится под знак числа. Знак положительного числа "+" кодируется нулем, а знак отрицательного числа "-" - единицей. Целые числа без знака в двухбайтовом формате могут принимать значения от 0 до 216-1 (до 65535), а со знаком - от -215 до +215-1, т.е. от -32768 до 32767.
Достоинствами естественной формы являются простота и наглядность представления чисел, простота алгоритмов реализации операций, а, следовательно, простота устройств и высокая скорость выполнения операций; недостатком - конечный диапазон представления величин. Неудобство представления чисел в форме с фиксированной точкой проявляется при решении задач, в которых фигурируют как очень малые, так и очень большие числа.
Запись чисел с плавающей точкой. Обработка очень больших и очень маленьких чисел производится в экспоненциальной форме. В этом случае положение запятой в записи числа может изменяться. Поэтому представление в памяти чисел в экспоненциальной форме называется представлением с плавающей точкой (запятой). Любое число А в экспоненциальной форме представляется в виде:
А = mА  qp,
qp,
где mA - мантисса числа, q - основание системы счисления, p - порядок числа.
Для однозначности представления чисел c плавающей точкой используется нормализованная форма, при которой мантисса отвечает условию:
q-1  |mА| < 1.
|mА| < 1.
Это означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.
Число в форме с плавающей точкой занимает в памяти компьютера четыре или восемь байт. При записи числа с плавающей точкой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Любое вещественное число в современных компьютерах представляется в экспоненциальной форме с нормализованной мантиссой. При этом мантисса является правильной двоичной дробью, а порядок - целым числом.
Пример. Преобразуйте десятичное число 888,888, записанное в естественной форме, в экспоненциальную форму с нормализованной мантиссой.
Решение. 888,888 = 0,888888  103
103
Нормализованная мантисса mА = 0,888888, порядок p = 3.
Кодирование текстовой информации.
В традиционных кодировках для кодирования одного символа используется 8 бит. Легко подсчитать по формуле 2.3, что такой 8-разрядный код позволяет закодировать 256 различных символов.
Присвоение символу определенного числового кода - это вопрос соглашения. В качестве международного стандарта принята кодовая таблица ASCII (American Standard Code for Information Interchange), кодирующая первую половину символов с числовыми кодами от 0 до 127 (коды от 0 до 32 отведены не символам, а функциональным клавишам). Данную таблицу можно найти в любом учебном пособии по информатике.
Национальные стандарты кодировочных таблиц включают международную часть кодовой таблицы без изменений, а во второй половине содержат коды национальных алфавитов, символы псевдографики и некоторые математические знаки. К сожалению, в настоящее время существуют пять различных кодировок кириллицы (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO), что вызывает дополнительные трудности при работе с русскоязычными документами.
Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 ("Код обмена информацией, 8-битный"). Эта кодировка применялась еще в 70-ые годы на компьютерах серии ЕС ЭВМ, а с середины 80-х стала использоваться в первых русифицированных версиях операционной системы UNIX.
Наиболее распространенной в настоящее время является кодировка Microsoft Windows, обозначаемая сокращением CP1251 ("CP" означает "Code Page", "кодовая страница").
От начала 90-ых годов, времени господства операционной системы MS DOS, остается кодировка CP866. Компьютеры фирмы Apple, работающие под управлением операционной системы Mac OS, используют свою собственную кодировку Mac. Кроме того, Международная организация по стандартизации (International Standards Organization, ISO) утвердила в качестве стандарта для русского языка еще одну кодировку под названием ISO 8859-5.
В конце 90-ых годов появился новый международный стандарт Unicode, который отводит под один символ не один байт, а два, и поэтому с его помощью можно закодировать не 256, а 65536 различных символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
Пример. Представьте в форме шестнадцатеричного кода слово "ЭВМ" во всех пяти кодировках. Воспользуйтесь таблицами CP866, Mac и ISO и компьютерным калькулятором для перевода чисел из десятичной в шестнадцатеричную систему счисления.
Последовательности десятичных кодов слова "ЭВМ" в различных кодировках составляем на основе кодировочных таблиц:
КОИ8-Р: 252 247 237
CP1251: 221 194 204
CP866: 157 130 140
Mac: 157 130 140
ISO: 205 178 188
Переводим с помощью калькулятора последовательности кодов из десятичной системы в шестнадцатеричную:
КОИ8-Р: FC F7 ED
CP1251: DD C2 CC
CP866: 9D 82 8C
Mac: 9D 82 8C
ISO: CD B2 BC
Кодирование графической информации.
Графические изображения, хранящиеся в аналоговой (непрерывной) форме на бумаге, фото- и кинопленке, могут быть преобразованы в цифровой компьютерный формат путем пространственной дискретизации. Это реализуется путем сканирования, результатом которого является растровое изображение. Растровое изображение состоит из отдельных точек (пикселей - англ. pixel образовано от словосочетания picture element, что означает элемент изображения), каждая из которых может иметь свой цвет.
Качество растрового изображения определяется его разрешением (количеством точек по вертикали и по горизонтали) и используемой палитрой цветов (16, 256, 65536 цветов и более).
Из данной формулы можно определить какое количество бит информации необходимо выделить для хранения цвета точки (глубину цвета I) для каждой палитры цветов (N - количество отображаемых цветов).
N=2I
Пример. Определить объем видеопамяти компьютера, который необходим для реализации графического режима монитора с разрешающей способностью 1024*768 точек и палитрой из 65536 цветов (High Color).
Глубина цвета составляет:
I = log265 536 = 16 бит
Количество точек изображения равно:
1024*768 = 786 432
Требуемый объем видеопамяти равен:
16 бит *786 432 = 12 582 912 бит = 1,2 Мбайта
Важнейшими характеристиками монитора являются размеры его экрана, которые задаются величиной его диагонали в дюймах (15", 17", 21" и т.д.) и размером точки экрана (0,25 мм или 0,28 мм), а разрешающая способность экрана монитора задается количеством точек по вертикали и горизонтали (640 на 480, 800 на 600 и т.д.). Следовательно, для каждого монитора существует физически максимально возможная разрешающая способность экрана.
Кодирование звуковой информации.
В аналоговой форме звук представляет собой волну с непрерывно меняющейся амплитудой и частотой. При преобразовании звука в цифровую дискретную форму производится временная дискретизация, при которой в определенные моменты времени амплитуда звуковой волны измеряется и квантуется, т.е. ей присваивается определенное значение из некоторого фиксированного набора. Данный метод называется еще импульсно-кодовой модуляцией PCM (Pulse Code Modulation).
Преобразование непрерывной звуковой волны в последовательность звуковых импульсов различной амплитуды производится с помощью аналого-цифрового преобразователя размещенного на звуковой плате. Современные 16-битные звуковые карты обеспечивают возможность кодирования 65536 различных уровней громкости или 16-битную глубину кодирования звука. Качество кодирования звука зависит и от частоты дискретизации - количества измерений уровня сигнала в единицу времени. Эта величина может принимать значения от 8 до 48 кГц.
Пример. Оцените информационный объем высококачественного стереоаудиофайла длительностью звучания 1 секунда, если "глубина" дискретизации 16 бит, а частота 24 кГц.
Информационный объем звукового файла длительностью в 1 секунду равен:
16 бит *24 000 = 384000 бит  47 Кбайт
47 Кбайт
Соответственно, чтобы узнать информационный объем файла, длительностью 1 минуту, нужно умножить полученное число на 60.
Формула Шеннона.
Количество информации как мера уменьшения неопределенности знаний. Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию.
Сообщения обычно содержат информацию о каких-либо событиях. Количество информации для событий с различными вероятностями определяется по формуле, которую предложил К.Шеннон в 1948 году:
где I - количество информации, N - количество возможных событий, pi - вероятности отдельных событий.
Если события равновероятны, то количество информации определяется по формуле:
I = log21/N
или из показательного уравнения: N = 2I.
Единицы измерения количества информации. За единицу количества информации принят 1 бит - количество информации, содержащееся в сообщении, уменьшающем неопределенность знаний в два раза.
Принята следующая система единиц измерения количества информации:
1 байт = 8 бит
1 Кбайт = 210 байт
1 Мбайт = 210 Кбайт = 220 байт
1 Гбайт = 210 Мбайт = 220 Кбайт = 230 байт
Пример. После экзамена по информатике, который сдавали ваши друзья, объявляются оценки ("2", "3", "4" или "5"). Какое количество информации будет нести сообщение об оценке учащегося A, который выучил лишь половину билетов, и сообщение об оценке учащегося B, который выучил все билеты.
Опыт показывает, что для учащегося A все четыре оценки (события) равновероятны и тогда количество информации, которое несет сообщение об оценке можно вычислить по формуле 2.2:
I = log24 = 2 бит
На основании опыта можно также предположить, что для учащегося B наиболее вероятной оценкой является "5" (p1 = 1/2), вероятность оценки "4" в два раза меньше (p2 = 1/4), а вероятности оценок "2" и "3" еще в два раза меньше (p3 = p4 = 1/8). Так как события неравновероятны, воспользуемся для подсчета количества информации в сообщении формулой 2.1:
I = -(1/2·log21/2 + 1/4·log21/4 + 1/8·log21/8 + 1/8·log21/8) бит = 1,75 бит
Вычисления показали, что при равновероятных событиях мы получаем большее количество информации, чем при неравновероятных событиях.