§6.
Преобразование случайных процессов динамическими системами
Случайные
явления, процессы обычно подвергаются различным воздействиям других протекании
их в конкретных системах и устройствах. К примеру, электрические сигналы –
случайные процессы – при прохождении через системы связи или управления могут
складываться ил ослабляться, интегрироваться или дифференцироваться.
Пусть
система S
осуществляет преобразование сигналов, функций, процессов, зависящих от времени t. Случайный процесс
![]() , подлежащий преобразованию данной системой,
называется входным сигналом, входным воздействием. Функция
, подлежащий преобразованию данной системой,
называется входным сигналом, входным воздействием. Функция ![]() , получаемая в результате преобразования S, называется входным сигналом,
реакцией системы S.
, получаемая в результате преобразования S, называется входным сигналом,
реакцией системы S.
К
примеру, при полете летального объекта, системы S, в качестве входного
сигнала-воздействия ![]() можно
рассматривать колебания атмосферы, а в качестве выходного сигнала
можно
рассматривать колебания атмосферы, а в качестве выходного сигнала ![]() – колебания
летального объекта относительно его центра масс.
– колебания
летального объекта относительно его центра масс.
Математически,
символически преобразование входного случайного сигнала-процесса ![]() , поступающего на вход системы S, в выходной сигнал-процесс
, поступающего на вход системы S, в выходной сигнал-процесс ![]() записывается в
виде соотношения
записывается в
виде соотношения
![]()
где
![]() – оператор,
задающий воздействие системы S.
– оператор,
задающий воздействие системы S.
В
общем случае воздействие зависит от момента его действия, чем и объясняется
зависимость оператора А от документа времени.
При
решении различных задач рассматриваются оператор интегрирования, оператор
решения дифференциального уравнения, оператор решения интегрального уравнения,
оператор возведения в степень и т.д.
Оператор
![]() называется
линейным однородным на классе функций С, если справедливо равенство
называется
линейным однородным на классе функций С, если справедливо равенство
![]()
При
любых числах ![]() и любых
функциях
и любых
функциях ![]() из С.
из С.
Линейным
неоднородным оператором L,
порожденным линейным однородным оператором ![]() и неслучайной
функцией
и неслучайной
функцией ![]() , называется оператор, действующий по закону
, называется оператор, действующий по закону
![]()
Как
мы уже знаем, свойства случайного процесса характеризуется с той или иной
полнотой моментными функциями, являющиеся результатом приложения к случайным
процессам понятия моментов случайных величин. К основным из них относятся функции математического ожидания
дисперсии и ковариационной функции. Приведем уравнения связи осредненных
характеристик случайных процессов при некоторых простейших их преобразованиях.
Возможность применения к данной случайной функции должна быть проверена в
каждом конкретном случае.
Если
![]() – линейный однородный оператор и y(t)=L{x(t)}, то осредненные характеристики
случайных процессов
– линейный однородный оператор и y(t)=L{x(t)}, то осредненные характеристики
случайных процессов ![]() и
и ![]() связаны
соотношениями
связаны
соотношениями
![]() (4)
(4)
![]() (5)
(5)
Пусть
L
есть линейный неоднородный оператор, заданный соотношением (3) и y(t)=L{x(t)}. Тогда имеют место формулы
![]() (6)
(6)
![]() (7)
(7)
При
преобразовании
![]() (8)
(8)
где
![]() ,
, ![]() – неслучайные функции, справедливы формулы
– неслучайные функции, справедливы формулы
![]() (9)
(9)
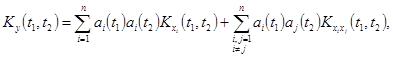 (10)
(10)
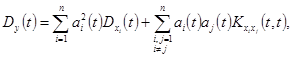 (11)
(11)
Если
в (8) случайные процессы ![]() взаимно некоррелированы, т.е.
взаимно некоррелированы, т.е. ![]() ,
, ![]() при любых
при любых ![]() и
и ![]() , то
, то
![]() (12)
(12)
![]() (13)
(13)
Нелинейные
операторы не обладают общими свойствами, которыми обладают линейные операторы. Каждый
нелинейный оператор обладает своими свойствами. Поэтому общих правил нахождения
характеристик случайного процесса полученного в результате преобразования
исходного случайного процесса x(t) нелинейной системой ![]() , нет.
, нет.
Задача 1.
На RC
– цепочку, изображенную на рисунке, подается случайное напряжение ![]() с характеристиками
с характеристиками ![]() и
и ![]() . Найти математическое ожидание, ковариационную
функцию и дисперсию напряжения y(t) на выходе RC-цепочки
. Найти математическое ожидание, ковариационную
функцию и дисперсию напряжения y(t) на выходе RC-цепочки
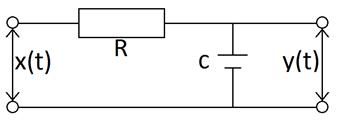
Решение.
Дифференциальное уравнение, описывающее связь между входящими и выходящими
напряжениями RC
цепочки, составляется на основе законов Кирхгофа и имеет вид
![]() (14)
(14)
Общее
решение линейного дифференциального уравнения первого порядка
![]()
имеет
вид
![]() (15)
(15)
где
С – произвольная постоянная .
При
каждом исходе ![]() для
произвольной реализации y(t) из (14) согласно (15) имеем, что
для
произвольной реализации y(t) из (14) согласно (15) имеем, что
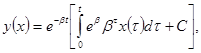
где С – произвольная постоянная. Так как в начальный момент
времени ![]() , то с=0 и имеем связь напряжений
, то с=0 и имеем связь напряжений
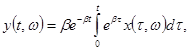 (16)
(16)
Таким
образом, случайный процесс, напряжение ![]() , является результатом применения к случайному
напряжению
, является результатом применения к случайному
напряжению ![]() оператора
оператора ![]() , действующего по закону
, действующего по закону
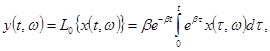 (17)
(17)
Нетрудно
убедиться, что ![]() , то есть оператор
, то есть оператор ![]() является
линейным однородным .
является
линейным однородным .
Определим
теперь характеристики напряжения ![]() на выходе
устройства. Математическое ожидание равно
на выходе
устройства. Математическое ожидание равно
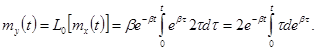
Поскольку
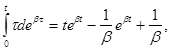 (18)
(18)
То
для математического ожидания получим выражение
![]()
Ковариационная функция ![]() согласно
формуле (5) равна
согласно
формуле (5) равна
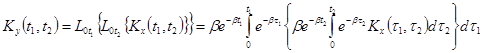
Найдем
внутренний интеграл; так как
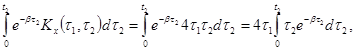
То
согласно (18) получим:
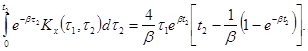
Следовательно
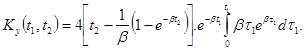
Применяя
к интегралу в полученном соотношении ту же формулу (18), мы получим функции
выходного напряжения ![]() :
:
![]()
Дисперсия
процесса равна
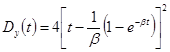
Интерес
представляют следующие асимптотики:
![]() ~
~![]()
![]() ~
~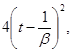
![]() ;
;
![]() ~
~![]()
![]() ,
,![]() ;
;
Задача 2.
На вход квадратичного детектора подается случайный процесс ![]() , где
, где ![]() и
и ![]() –
некоррелированные, центрированные, нормально распределенные случайные величины
с дисперсиями
–
некоррелированные, центрированные, нормально распределенные случайные величины
с дисперсиями ![]() . На выходе детектора получается случайный процесс
. На выходе детектора получается случайный процесс ![]() . Найти характеристики случайного процесса
. Найти характеристики случайного процесса ![]() .
.
Решение.
Найдем характеристики искомого процесса ![]() . По условию задачи
. По условию задачи ![]() и потому
и потому ![]() .
.
В
силу центрированности случайного процесса имеем:
![]()
![]() .
.
Так
как ![]() ,
, ![]() , то
, то ![]() .
.
Дисперсия
![]()
Найдем
теперь характеристики выходного процесса
![]()
Согласно
свойствам случайных величин ![]() и
и ![]() очевидным
образом имеем:
очевидным
образом имеем:
![]()
Процесс
![]() можно представить
в следующем виде
можно представить
в следующем виде
![]()
Введем
следующие случайные процессы:
![]() ,
,
![]() ,
,
![]() .
.
В
результате принятых обозначений случайный процесс ![]() представляется
в виде суммы трех центрированных случайных процессов:
представляется
в виде суммы трех центрированных случайных процессов:
![]() .
.
Определим
ковариацию функции ![]() процесса y(t). Согласно принятым обозначениям
имеем представление
процесса y(t). Согласно принятым обозначениям
имеем представление
![]()
Приведем
теперь некоторые соотношения, которым удовлетворяют случайные величины ![]() и
и ![]() . Так как
. Так как ![]() и
и ![]() распределены
нормально с параметрами
распределены
нормально с параметрами ![]() и
и ![]() , то
, то ![]()
Отсюда
непосредственно следует , что ![]()
В
случае некоррелированных случайных величин ![]() ~
~![]() ,
, ![]() ~
~![]() справедливы равенства,
справедливы равенства,
![]()
![]()
![]() ,
,
Поэтому
имеют место следующие равенства:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Поэтому
![]() ,
,
т.е.
![]()
Дисперсия
процесса равна
![]()
Осредненные характеристики входного x(t) и выходного y(t) процессов связаны соотношениями
![]()
Задача 3.
На вход квадратичного детектора поступает случайный процесс
![]()
где
![]() и
и ![]() –
некоррелированные, центрированные нормально распределенные случайные величины с
дисперсиями
–
некоррелированные, центрированные нормально распределенные случайные величины с
дисперсиями ![]() . Найти характеристики случайного процесса
. Найти характеристики случайного процесса ![]() на выходе
детектора
на выходе
детектора
Решение.
Как нетрудно заметить, мы в данном случае имеем обобщение предыдущей задачи.
Сначала определим характеристики исходного процесса x(t) для сравнения с характеристиками
полученного на выходе сигнала.
Поскольку
![]() для любого
для любого ![]() , то очевидным образом
, то очевидным образом
![]()
Поэтому
в нашем случае ![]() и потому
и потому ![]()
Согласно
условию задачи ![]() ,
, ![]() , а
, а ![]() ,
, ![]() при
при ![]()
С
учетом этих моментов получаем следующее представление для ковариоционной
функции:
![]()
Дисперсия процесса равна
![]()
Найдем
теперь характеристики преобразования сигнала. Ясно, что
![]()
В силу некоррелированности случайных величин ![]() ,
, ![]() очевидным
образом получим, что
очевидным
образом получим, что
![]()
Значит,
для центрированного процесса ![]() справедливо
представление
справедливо
представление
![]()
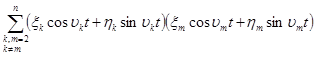
Проводя
последовательно соответствующие выкладки, мы придем к следующим формулам
![]() ,
,
![]()
1.
Случайный процесс ![]() , где
, где ![]() и
и ![]() – независимы и равномерно распределенные
на отрезке [-2;2] случайные величины, преобразовываются по закону
– независимы и равномерно распределенные
на отрезке [-2;2] случайные величины, преобразовываются по закону
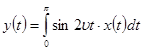
Найти
характеристики выходного сигнала y(t)
2.
На вход квадратичного детектора
поступает случайный сигнал ![]() , где
, где ![]() и
и ![]() – независимые случайные
величины, распределенные по показательному закону с параметром
– независимые случайные
величины, распределенные по показательному закону с параметром ![]() . Найти характеристики выходного сигнала.
. Найти характеристики выходного сигнала.
3.
На вход линейной динамической системы,
описываемой уравнением ![]() , поступает случайный сигнал
, поступает случайный сигнал ![]() с
характеристиками
с
характеристиками ![]() ,
, ![]() .
.
Найти
характеристики ![]() ,
, ![]() и
и ![]() на выходе
системы.
на выходе
системы.
4.
Динамическая система суммирует
поступающие случайные сигналы ![]() по закону
по закону
![]()
Найти
характеристики выходного сигнала y(t), если на систему поступили
случайные синусоиды ![]() , где
, где ![]() – независимые
амплитуды с характеристиками
– независимые
амплитуды с характеристиками ![]() ,
, ![]() .
.
Найти характеристики ![]() ,
, ![]() и
и ![]() случайного
процесса
случайного
процесса ![]() , где
, где ![]() и
и ![]() – заданные функции,
а x(t) – дифференцируемая случайная
функция с известными
– заданные функции,
а x(t) – дифференцируемая случайная
функция с известными ![]() и
и ![]() .
.