§ 3. Осредненные характеристики случайного процесса

Математическим ожиданием и дисперсией случайного процесса , называются такие неслучайные функции и , которые для каждого равны соответственно математическому ожиданию и дисперсии сечения процесса в этот момент времени:

, .

Ковариационной функцией случайного процесса называется неслучайная функция двух переменных

.

Корреляционной функцией случайного процесса называется функция

.

Для любых ковариационная функция численно равна ковариации сечений случайного процесса и в моменты времени и характеризует степень линейной зависимости между сечениями.

Взаимные ковариационная функция и корреляционная функция двух случайных процессов определяются по формулам

,

.

Если и есть соответственно одномерная и двумерная функции распределения случайного процесса, то

,

,

.

При наличии одномерной и двумерной плотностей распределений и случайного процесса его осредненные характеристики определяются формулами

,

,

.

Ковариационная функция удовлетворяет следующим свойствам:

1. Симметричность: .

2. Ограниченность: .

3. Неотрицательная определенность: при любом и любой комплекснозначной функции справедливо неравенство:

.

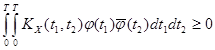Согласно соотношениями (1) из неравенства Коши-Буняковского следует, что для существования , , при всех достаточно выполнение условия

. (2)

Случайный процесс , , удовлетворяющей условию (2), называется процессом с конечным моментом второго порядка или гильбертовым случайным процессом.

Задача 1. Случайный процесс задан уравнением , , где - действительная случайная величина с математическим ожиданием и дисперсией , и - неслучайные функции на . Найти , , .

Решение. По определению очевидным образом имеем, что

.

Положим .Тогда в данном случае и потому по определению имеем:

,

т.е. .

Дисперсия процесса .

Задача 2. Случайный процесс имеет вид

, ,

где - действительные некоррелированные случайные величины с известными параметрами , , а - заданные на неслучайные функции. Найти , и .

Решение. По определению

,

то есть

.

Аналогично по определению

.

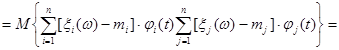
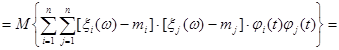
Так как , - некоррелированные случайные величины, то

Следовательно,

,

а

.

Задача 3. Задана двумерная плотность случайного процесса в виде

.

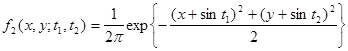Вычислить основные характеристики процесса , и .

Решение. Определим одномерную плотность распределения по формуле

.

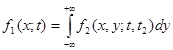Согласно этой формуле

.

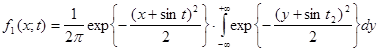Проведя замену , мы получим

.

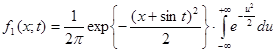Но поскольку

,

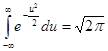то для одномерной плотности получим представление

.

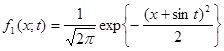Математическое ожидание процесса равно

.

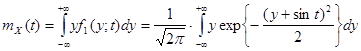Как и выше, проведя замену , получим

,

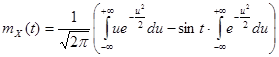откуда имеем, что

.

Найдем дисперсию случайного процесса. По определению

.

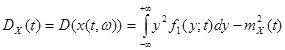Поэтому

.

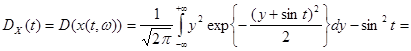
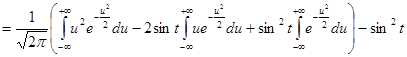Второй интеграл в полученном выражении равен нулю. Следовательно,

,

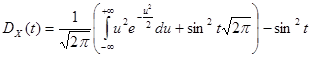
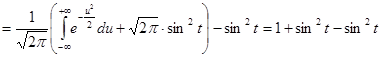то есть

.

Заметим, что при

.

Пусть теперь . По определению ковариационной функции

.

Как нетрудно видеть из выражения для двумерной плотности, выполняется равенство

.

Следовательно, сечения и независимы при и потому

.

Значит, при и потому для ковариационной функции получаем выражение

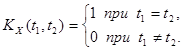
1. Найти математическое ожидание, дисперсию и ковариационную функцию случайного процесса , где - случайная величина, равномерно распределенная на отрезке .

2. Найти осредненные основные характеристики синусоиды постоянной частоты со случайной амплитудой , если и .

3. Случайный процесс задан уравнением

,

где и - некоррелированные случайные величины с , , , .Найти осредненные характеристики процесса.

4. Дан случайный процесс

,

где и - случайные величины с , , , , . Найти математическое ожидание и ковариационную функцию процесса.

5. Найти ковариационную функцию процесса , где случайные величины , независимы, имеет распределение , а имеет равномерное распределение на .

6. Найти математическое ожидание и ковариационную функцию комплексного случайного процесса , где и -независимые случайные величины, , , а случайная величина распределена по закону Коши с плотностью распределения , где .