ГЛАВА I. Случайные процессы и их преобразования.

§ 1. Случайные функции, процессы. Конечномерные распределения

Пусть есть произвольное множество¸ а - -алгебра его подмножеств. Тогда пара называется измеримым пространством.

На множестве различными способами можно определить вероятность . После введения вероятности элементы множества и множества из -алгебры становятся случайными. Тройка называется вероятностным пространством или вероятностной моделью. Как нетрудно видеть, на одном и том же множестве можно построить различные вероятностные пространства, модели.

Наименьшая -алгебра ,содержащая систему множеств числовой прямой, являющихся конечной суммой непересекающихся промежутков вида , называется борелевской -алгеброй множеств числовой прямой и обозначается символом .

Определение. Пусть есть вероятностное пространство, - числовая прямая с системой борелевских множеств. Действительная функция , определенная на , называется - измеримой функцией или действительной случайной величиной, если для любого множества из выполняется включение .

Определение. Пусть - вероятностное пространство, - измеримое пространство, - некоторое множество. Случайной функцией , определенной на множестве и вероятностном пространстве , называется отображение , являющееся при каждом из измеримым отображением в , т. е. такое, что для любого множества и фиксированного справедливо включение

.

Если множество есть временная ось или ее подмножество , то случайная функция называется случайным процессов. Обычно случайные процессы обозначаются символами , , и т.д. Как правило, второй аргумент не указывается. В дальнейшем будем рассматривать действительные случайные процессы, т. е. случай .

Случайная величина , в которую обращается случайный процесс при , называется сечением случайного процесса, соответствующего данному значению аргумента . Сечение есть совокупность всевозможных значений случайного процесса, принимаемых им в данный момент времени.

Реализацией случайного процесса называется неслучайная функция , в которую обращается случайный процесс в результате опыта, исходом которого является случайное событие . Реализацию называют также траекторией процесса.

Пусть дан случайный процесс , .При фиксированном закон распределения случайной величины называется одномерным законом распределения процесса. Одномерные распределения образуют семейство одномерных распределений процесса

, , . (1)

Для процессов с дискретным распределением всех сечений одномерный закон распределения задается, как обычно, таблицей всех возможных значений данного сечения с их вероятностями:

, , …, ,…,

, , …, ,…, (2)

, .

При любом натуральном и любых из и из аналогично определяется семейство –мерных распределений процесса:

. (3)

Разумеется, семейство -мерных распределений (3) удовлетворяет следующим условиям согласованности:, (4)

, (5)

где - любая перестановка индексов .

Теорема (Колмогорова). Для любого согласованного семейства распределений (3) можно построить вероятностное пространство и семейство определенных на нем случайных величин , так, чтобы данное семейство распределений было распределением последовательности случайных величин .

Задача 1. Случайный процесс является случайный функцией вида , , где ~ - случайная величина, равномерно распределена на отрезке .Описать множество сечений и траекторий случайного процесса.

Решение. Пусть есть произвольный фиксированный момент времени. Так как и , то или .

Итак, значения сечения принадлежат отрезку , причем оно, сечение, также равномерно распределено на этом отрезке.

При произвольном случайном исходе траектория имеет вид . Уравнение есть уравнение прямой с тангенсом угла наклона , проходящей через начало координат.

Поэтому траектории процесса , т. е. неслучайные функции являются прямыми линиями, выходящими из точки со случайным тангенсом угла наклона, равным .

Случайный процесс называется регулярным, если ее траектории в каждой точке непрерывны справа и имеют конечные пределы слева.

Процесс регулярен, т. к. все его траектории непрерывны.

Задача 2. Пусть случайный процесс имеет вид

при , ; ,

где , - последовательность конечных случайных величин. Описать траектории случайного процесса . Является ли этот процесс регулярным?

Решение. При фиксированном мы имеем фиксированную числовую последовательность , т. е. конкретную функцию , ,

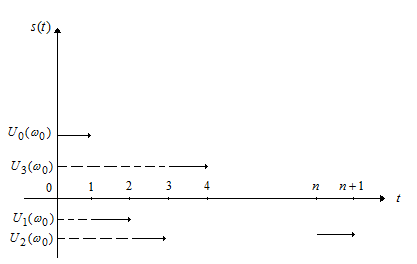
Как нетрудно видеть, траектории процесса есть кусочно-постоянные функции, испытывающие разрывы в точках Эти функции непрерывны справа, имеют пределы слева, равные

.

Поскольку , т. е. по условию, то процесс регулярен.

Задача 3. Случайный процесс задан соотношением

, ,

где - некоторая случайная с функцией распределения , а -- положительная неслучайная функция. Найти семейство конечномерных распределений процесса .

Решение. По определению - мерной функции распределения процесса

.

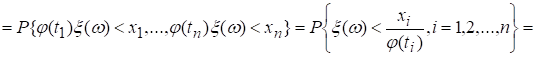
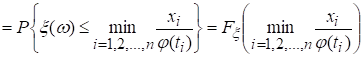Итак,

.

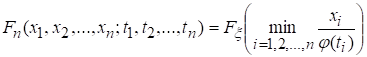Значение функции от - переменных равно значение функции от одной переменной , где .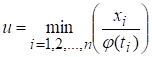

1. Случайный процесс задан уравнением , , где - случайная величина, равномерно распределенная на промежутке . Описать множество сечений и траекторий случайного процесса.

2. Описать множество траекторий и сечений случайного процесса , , где - случайна величина, распределенная по закону Пуассона с параметром .

3. Случайный процесс задан соотношением , , где – случайная величина, имеющая показательное распределение с параметром . Найти семейство конечномерных распределений.

4. Случайный процесс имеет вид , , где -- случайная величина, равномерно-распределенная на . Найти одномерную функцию распределения и одномерную плотность этого процесса.

5. Случайный процесс задан в виде , где - случайная величина непрерывного типа, подчиняющаяся закону , а - неслучайная константа. Найти одномерную плотность .

6. Случайный процесс задан в виде , где и - независимые случайные величины, подчиняющиеся одному и тому же закону распределения . Найти одномерную плотность .

7. Заданы плотности и независимых случайных величин и . Найти одномерную плотность процесса , .