§5. Интегрирование случайных функций

Траектория случайного процесса является неслучайной функцией и интеграл от нее определяется как обычный интеграл Римана. Потраекторная интегрируемость случайного процесса, поэтому вводится следующим образом.

Определение. Случайная функция x(t) называется интегрированной потраекторно на отрезке [a,b], если почти все её траектории интегрируемы на этом отрезке, т. е.

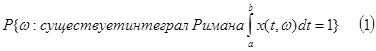
Введем теперь понятие интеграла от случайной функции в среднеквадратическом смысле. Пусть случайная функция x(t) определена на . На отрезке построим разбиение произвольное и на каждом из промежутков этого разбиения выберем произвольную точку .

Определение. Если при и существует предел в среднеквадратическом

Не зависящий от способа разбиения и выбора точек , то случайная x(t) называется с. к. – интегрируемой на [a,b], а случайная величина называется ее с. к. – интегралом по [a,b] и обозначается символом.

Имеет место следующий простой критерий с. к. – интегрируемости случайной функции.

Теорема 1. Для того чтобы случайная функция x(t) была с. к. – интегрируема на отрезке [a,b], необходимо и достаточно, чтобы существовал конечный интеграл

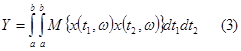
Нетрудно убедиться в том, что существование конечного интервала (3) эквивалентно существованию интегралов Римана

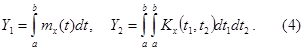
Для с. к. – интеграла справедливы многие свойства обычного интеграла от неслучайных функций. Приведем три из них, часто используемые при преобразования .

1. Линейность интеграла: если – неслучайные коэффициенты, а – с. к. – интегрируемые на случайные функции, то

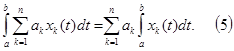
2. Формула интегрирования по частям: если – непрерывно дифференцируемая неслучайная функция, а x(t) случайная функция, имеющая с. к. – непрерывную с. к. – производную, то

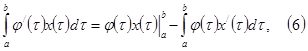
3. Правило дифференцирования по верхнему пределу: если x(t) – с. к. непрерывная случайная функция, то с. к. – производная, случайной функции

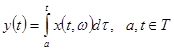
то с единичной вероятностью выполняется равенство

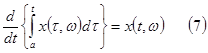
Приведем в едином утверждении несколько равенств, связывающих интеграл от случайного процесса с его осредненными характеристиками.

Теорема 2. Если случайная функция с. к. – интегрируема на

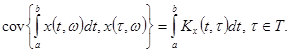
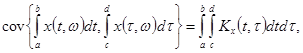
Задача 1. Доказать, что всякая случайная x(t), с. к. – непрерывна на конечном промежутке [a,b], является с. к. – интегрируемой на [a,b].

Решение. Случайный процесс x(t) с. к. – непрерывен на отрезке [a,b] тогда и только, когда математическое ожидание непрерывно на [a,b], а ковариационная функция непрерывна на диагонали, при

Следовательно, согласно условию задачи функция непрерывна на [a,b], поэтому интервал определяемый первой формулой из (4), существует как интервал от непрерывной функции на конечном отрезке. Поскольку ковариационная функция непрерывна на диагонали, при , то она непрерывна и на квадрате . Значит, существует и второй интервал из (4). Согласно теореме 1, функция является с. к. – интегрируемой.

Задача 2. Случайный процесс задается уравнением где и – центрированные некоррелированные случайные величины с конечной дисперсией Определить осредненные характеристики процесса

Решение. Поскольку и – центрированные случайные величины, то и потому очевидными образом имеем: .

Так как

,

то

Согласно условию задачи имеем, что

Следовательно, т.е. .

Найдем теперь характеристики процесса y(t). Математическое ожидание .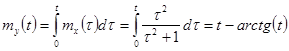

Ковариационная функция

.

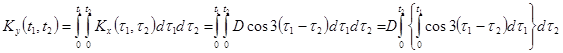Интегрирование по переменной приводит к равенству .

Проводя интегрирование по второй переменной мы получим окончательное выражение для ковариационной функции:

Полагая полученном выражении, находим дисперсию: .

Задача 3. Пусть функция есть с. к. непрерывная случайная функция. Доказать, что при любом и заданном почти всюду на справедливо равенство

.

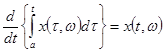Решение. Пусть приращение h таково, что , . Тогда для приращения случайной функции 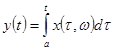получим равенство

.

Докажем, что

(8)

При

.

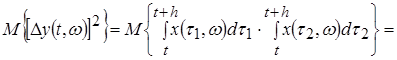
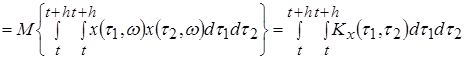В силу с. к. – непрерывности x(t) ковариационная функция непрерывна и потому из последнего равенства получаем равенство –

.

Точно также можно показать, что имеет место соотношение

.

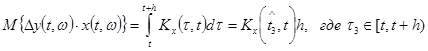Следовательно, имеет место представление

(9)

Поскольку , то при аргументы . Тогда в силу непрерывности функции при имеем:

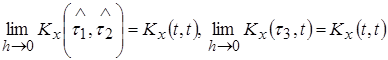
Из последних соотношений согласно (9) получим, что имеет место равенство (8), т.е. .

Итак, мы показали требуемое при

Пусть теперь и . В этом случае

(10)

Производная от второго интеграла в (10) существует в силу непрерывности , а производная от первого интеграла существует по доказанному нами. Следовательно, требуемое нами доказать утверждение полностью обоснованно.

Задача 4. На ход интегратора, работающего по принципу 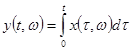, где – произвольная реализация случайного процесса на входе, поступает случайный процесс x(t) с ковариационной функцией и математическим ожиданием . Найти математическое ожидание и дисперсию случайного процесса математическое ожидание и дисперсию случайного процесса y(t) на выходе интегратора.

Решение. Математическое ожидание случайного процесса y(t) на выходе интегратора равно

,

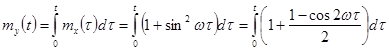Оттуда имеем: .

Ковариационная функция равна

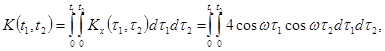
т.е.

.

1. Случайный процесс задан каноническим разложением , где и – случайные величины с одной и той же дисперсией Д. Найти математическое ожидание, дисперсию и ковариационную функцию процесса

2. Случайный процесс задан каноническим разложением с характеристиками , . Найти математическое ожидание и дисперсию процесса

3. На вход интегратора, работающего по принципу , где – поступающий случайный сигнал, процесс, поступает случайный процесс x(t) с осредненными характеристиками , . Найти осредненные характеристики процесса y(t) на выходе интегратора.

4. Задана ковариационная функция случайного процесса x(t). Показать, что взаимная ковариационная функция случайных процессов x(t) и может быть представлена в виде .

5. Ковариационная функция случайного процесса x(t) задана в виде . Найти взаимную ковариационную функцию случайных процессов x(t) и .