МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное
образовательное учреждение высшего профессионального образования
«Дагестанский государственный
университет»
Факультет математики и компьютерных наук
Кафедра математического анализа
Курс лекций по дисциплине
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
(II семестр)
Направление
09.03.02 – Информационные системы и технологии
Профиль подготовки
Информационные системы
и технологии
Уровень высшего образования: бакалавр
Форма обучения: очная
Автор-составитель
Магомедова
Вазипат Гусеновна
Махачкала - 2017
Оглавление
Тема 1. Неопределенный интеграл. Основные
методы интегрирования
Тема 2. Интеграл Римана. Суммы Дарбу
Тема 3. Свойства интеграла Римана. Теоремы о среднем.
Основная теорема интегрального исчисления
Тема
4. Методы замены переменной и интегрирования по
частям
Тема 5. Несобственные интегралы.
Признаки сходимости
Тема 6. Двойной интеграл. Свойства. Вычисление
Тема 7. Числовые ряды. Их свойства
Тема 8. Сходимость рядов с неотрицательными членами
Тема 9. Знакопеременные ряды. Их сходимость
Тема 10. Степенной ряд. Функциональные свойства
Модуль 3. Дифференциальные уравнения
Тема 11. Дифференциальные уравнения первого
порядка
Тема 12. Линейные дифференциальные уравнения с
постоянными коэффициентами
Тема 13. Приложения интегралов, рядов и
дифференциальных уравнений
Модуль 1. Интегралы
Тема 1. Неопределенный интеграл. Основные методы интегрирования
Функция ![]() называется первообразной
для функции
называется первообразной
для функции ![]() на промежутке
на промежутке ![]() , если
, если ![]() для любого
для любого ![]() .
.
Свойство первообразных.
Теорема 1. Если ![]() - первообразная для
функции
- первообразная для
функции ![]() на промежутке
на промежутке ![]() , то
, то ![]() (
(![]() - константа) - тоже первообразная для функции
- константа) - тоже первообразная для функции ![]() на промежутке
на промежутке ![]() .
.
Доказательство. ![]() .
.
Теорема 2. Пусть ![]() - две первообразных
для функции
- две первообразных
для функции ![]() , тогда они различаются на некоторую константу (
, тогда они различаются на некоторую константу (![]() - константа).
- константа).
Рассмотрим функцию ![]() , она непрерывна и дифференцируема на всей числовой оси, как
и функции
, она непрерывна и дифференцируема на всей числовой оси, как
и функции ![]() . Тогда для любых конечных значений
. Тогда для любых конечных значений ![]() по формуле конечных
приращений Лагранжа
по формуле конечных
приращений Лагранжа ![]() .
.
Следовательно, ![]()
Неопределенным интегралом ![]() (интеграл от функции
(интеграл от функции ![]() по
по
![]() ) называется совокупность всех
первообразных функций для функции
) называется совокупность всех
первообразных функций для функции ![]() .
.
![]() .
.
Функция ![]() , стоящая под знаком интеграла, называется подынтегральной
функцией, а выражение
, стоящая под знаком интеграла, называется подынтегральной
функцией, а выражение ![]() - подынтегральным
выражением.
- подынтегральным
выражением.
Свойства неопределенного интеграла.
1) ![]()
2) ![]() .
.
Запишем таблицу значений
ряда неопределённых интегралов, получающуюся непосредственно из соответствующей
таблицы производных элементарных функций.
1.  .
.
Если число a таково,
что степень ![]() имеет смысл и для всех
x £ 0, то формула 1 справедлива на любом
промежутке.
имеет смысл и для всех
x £ 0, то формула 1 справедлива на любом
промежутке.
2. ![]() .
.
3.  .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10. ![]() .
.
11.  .
.
12.  .
.
13. ![]() .
.
14.  .
.
15.  .
.
16.  .
.
Пример. Вычислить интеграл  .
.
Оглавление
Основные методы интегрирования
Метод подведения под дифференциал.
Пусть известен интеграл ![]() (
(![]() - первообразная для функции
- первообразная для функции ![]() ). Тогда
). Тогда ![]()
Доказательство. ![]() по
теореме о сложной функции. Следовательно, функция
по
теореме о сложной функции. Следовательно, функция ![]() и
и ![]() являются
первообразными для функции
являются
первообразными для функции ![]() и, по теоремам о первообразных, различаются на константу.
и, по теоремам о первообразных, различаются на константу.
Этот метод применяется часто. Например, ![]() ,
,  .
.
Это – универсальный метод, метод подведения под дифференциал является
частным случаем метода замены переменной.
Теорема. Пусть функция ![]() непрерывно
дифференцируема в некоторой области и имеет непрерывно дифференцируемую
обратную функцию
непрерывно
дифференцируема в некоторой области и имеет непрерывно дифференцируемую
обратную функцию ![]() . Тогда
. Тогда ![]() где
где ![]() .
.
Доказательство. Дифференцируя обе части, используя
теоремы о производной сложной функции и инвариантность формы записи первого
дифференциала, получим тождество дифференциалов.
![]() , где
, где ![]() . Из него следует равенство интегралов в левой и правой
частях.
. Из него следует равенство интегралов в левой и правой
частях.
Заметим, что требования к обратной функции нужны, чтобы суметь
возвратиться обратно, от переменной ![]() к переменной
к переменной ![]() .
.
Для вычисления интегралов вида ![]() , если вместо него удобно вычислять интеграл
, если вместо него удобно вычислять интеграл ![]() , пользуются методом интегрирования по частям.
, пользуются методом интегрирования по частям.
Теорема. Если функции ![]() и
и ![]() дифференцируемы на
некотором промежутке и на этом промежутке существует интеграл
дифференцируемы на
некотором промежутке и на этом промежутке существует интеграл ![]() , то на нём существует и интеграл
, то на нём существует и интеграл ![]() , причём
, причём
![]() .
.
Доказательство. Докажем справедливость этой формулы.
Дифференцируя произведение функций, получим ![]() или
или ![]() .
.
Интегралы левой и правой частей существуют (![]() ).
).
Интегрируя, получим нужное соотношение.
Примеры.
1. ![]() .
.
2.  .
.
Здесь взяли  .
.
3. ![]()
Вычислим интегралы ![]() ,
, ![]() .
.
4. ![]() , 5.
, 5. ![]()

 .
.
Теперь, подставляя второй интеграл в первый, получим
![]() .
.
Аналогично, подставляя первый интеграл во второй,
получим
![]() .
.
Интегрирование выражений, содержащих квадратный трехчлен.
Квадратный трехчлен ![]() , выделяя полный квадрат, можно привести к виду
, выделяя полный квадрат, можно привести к виду
![]() =
=  ,
,
где ![]() ,
,  .
.
Знак «+» выбирается, если ![]() , знак «-» выбирается, если
, знак «-» выбирается, если ![]() . Если
. Если ![]() .
.
1.  .
.
Если ![]() , то
, то  .
.
Если ![]() , то
, то  .
.
Если ![]() , то
, то ![]()
2.
 .
.
Если ![]() ,
,![]() , то под корнем стоит
отрицательное число, интеграл в функциях действительной переменной вычислить не
удастся.
, то под корнем стоит
отрицательное число, интеграл в функциях действительной переменной вычислить не
удастся.
Если ![]() ,
, ![]() , то
, то  =
= ![]() .
.
Если ![]() ,
, ![]() , то
, то ![]() =
= ![]() .
.
Если ![]() , то
, то  .
.
Если ![]() , то
, то  =
= .
.
3. 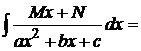
 =
=
 .
.
Интеграл ![]() вычислен в п.1.
вычислен в п.1.
4. ![]() =
=
![]() .
.
Интеграл  вычислен в п.2.
вычислен в п.2.
Примеры.
1. 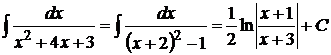
2. 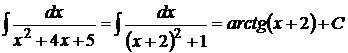
3. 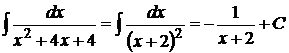
4. 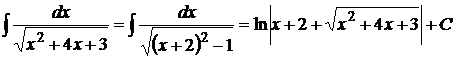
5. 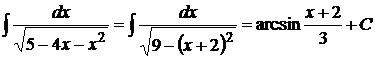
Оглавление
Интегрирование рациональных функций
Рациональная функция – это отношение
двух многочленов (полиномов).
Утверждение 1. Если
степень числителя больше либо равно степени знаменателя, то рациональную функцию можно привести к сумме некоторого многочлена
и рациональной функции, у которой степень числителя будет меньше степени
знаменателя.
Доказательство основано на правиле деления многочленов с остатком,
например, на алгоритме деления многочленов «уголком».
Пример.  .
.
Отсюда следует, что ![]() .
.
Интеграл от многочлена равен по свойствам линейности интеграла сумме
произведений интегралов от степенных функций на постоянные коэффициенты.
Интеграл от степенной функции легко вычислить по таблице интегралов.
Рассмотрим рациональную функцию ![]() .
.
Многочлен ![]() – знаменатель рациональной дроби может иметь действительный корень
– знаменатель рациональной дроби может иметь действительный корень
![]() некоторой
некоторой ![]() - ой кратности. Тогда
- ой кратности. Тогда ![]()
![]() , где многочлен
, где многочлен ![]() уже не имеет корня
уже не имеет корня ![]() . В этом случае из рациональной дроби можно выделить
элементарную рациональную дробь вида
. В этом случае из рациональной дроби можно выделить
элементарную рациональную дробь вида ![]() .
.
Утверждение 2. Пусть ![]() - действительный
корень
- действительный
корень ![]() - ой кратности полинома
- ой кратности полинома ![]() – знаменателя рациональной дроби. Тогда
– знаменателя рациональной дроби. Тогда
![]() =
= ![]()
![]() , где многочлен
, где многочлен ![]() уже не имеет корня
уже не имеет корня ![]() .
.
Доказательство. Приведем дроби к общему знаменателю ![]() и приравняем числители
полученных дробей.
и приравняем числители
полученных дробей.
![]() . Тогда выражение
. Тогда выражение ![]() должно делиться на
должно делиться на ![]() , т.е.
, т.е. ![]() . Этого можно добиться, выбрав
. Этого можно добиться, выбрав ![]() .
.
Замечание 1. В условиях утверждения 2 рациональную
дробь можно представить в виде
![]() где
где ![]() не имеет корня
не имеет корня ![]() .
.
Доказательство. Применим лемму 2 ![]() раз и получим
указанное разложение.
раз и получим
указанное разложение.
Полином ![]() – знаменатель рациональной дроби может иметь пару комплексно
сопряженных корней
– знаменатель рациональной дроби может иметь пару комплексно
сопряженных корней ![]()
![]() -ой кратности. Тогда
-ой кратности. Тогда

При этом ![]() уже не являются
корнями полинома
уже не являются
корнями полинома ![]() . В этом случае из рациональной дроби тоже можно выделить
некоторую элементарную рациональную дробь вида
. В этом случае из рациональной дроби тоже можно выделить
некоторую элементарную рациональную дробь вида ![]() .
.
Утверждение 3. Пусть ![]() – знаменатель рациональной дроби
– знаменатель рациональной дроби ![]() имеет пару комплексно
сопряженных корней
имеет пару комплексно
сопряженных корней ![]()
![]() - ой кратности. Тогда рациональную дробь можно представить в
виде
- ой кратности. Тогда рациональную дробь можно представить в
виде
![]() =
= ![]()
 , где
, где ![]() уже не являются
корнями полинома
уже не являются
корнями полинома ![]() .
.
Доказательство. Приведем дроби к общему знаменателю и приравняем
числители полученных дробей.
![]() =
= .
. ![]() должно делиться как на
должно делиться как на ![]() , так и на
, так и на ![]() . Поэтому
. Поэтому
![]() ,
, ![]() , где
, где ![]() =
=![]() ,
, ![]() =
=![]() .
.
Отсюда имеем систему уравнений для определения констант ![]()
 ,
,
 .
.
Определитель этой системы равен ![]() , так как корни комплексные и
, так как корни комплексные и ![]() . Поэтому система имеет единственное решение.
. Поэтому система имеет единственное решение.
Замечание 2. В условиях утверждения 2 рациональную
дробь можно представить в виде
![]() =
= ![]() +
+![]() + …+
+ …+![]() +
+ ![]() ,
,
где ![]() уже не являются
корнями полинома
уже не являются
корнями полинома ![]() .
.
Теорема. Рациональная функция может быть
представлена в виде
![]() =
=![]() +
+![]() +…+
+…+![]() +…+
+…+![]() +
+![]() + …+
+ …+![]() + …+
+ …+![]() ,
,
где ![]() - простой действительный корень
- простой действительный корень ![]() ,
, ![]() - действительный корень
- действительный корень ![]() кратности
кратности ![]() ,
, ![]() - пара комплексно сопряженных корней кратности
- пара комплексно сопряженных корней кратности ![]()
![]() (комплексно сопряженные
корни
(комплексно сопряженные
корни ![]() ),
), ![]() - простая пара комплексно сопряженных корней
- простая пара комплексно сопряженных корней ![]() (корни
(корни ![]() ).
).
Замечание 3. Задача интегрирования рациональной
функции сводится к задачам интегрирования элементарных рациональных дробей
четырех типов
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4)![]() .
.
Способы вычисления
коэффициентов при разложении рациональной дроби на
элементарные.
Пример. 
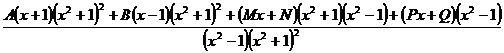
Теперь надо приравнивать многочлены в числителях дробей и определять
неизвестные коэффициенты A, B, M, N, P, Q.
Это можно сделать двумя способами.
1 способ – приравнивать коэффициенты
при одинаковых степенях переменной, составлять и решать систему уравнений.
X5| 3=A+B+M
X4| 1=A-B+N
X3| 7=2A+2B+P
X2| 2=2A-2B+Q Решение системы A=2, B=1, M=N=Q=0, P=1.
X |2=A+B-N-P
1 |1=A-B-N-Q
2 способ – задавать значения
неизвестной, вычислять значения числителей и составлять систему уравнений.
X=1 | 16=8A
X= -1| -8=-8B
X=0
| 1=A-B-N-P
X=2
| 181=75A-25B+30M+15N+6P+3Q
X=-2 | -96= -25A-75B-30M+15N-6P+3Q
X=-3 | -824= -200A –400B-240M –80N
–24P+8Q
Решая эту систему уравнений, получим то же решение A=2, B=1, M=N=Q=0, P=1.
Какой способ применять – зависит от того, где получается более простая и
удобная для решения система уравнений.
В данном примере вторая система сложнее первой.
![]() Интегрирование
простейших рациональных дробей.
Интегрирование
простейших рациональных дробей.
1)
![]() ,
,
2)
![]()
3) ![]()
![]() =
=
![]() (пример рассмотрен во
второй лекции). Для того, чтобы вычислить интеграл от
дроби в п.3, достаточно в соответствующем примере второй лекции обозначить
коэффициенты другими буквами.
(пример рассмотрен во
второй лекции). Для того, чтобы вычислить интеграл от
дроби в п.3, достаточно в соответствующем примере второй лекции обозначить
коэффициенты другими буквами.
4)
![]()
![]()
![]() =
= =
=
![]() , где
, где ![]() .
.
Вычислим интеграл ![]() .
.
![]() .=
.= 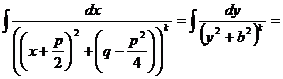
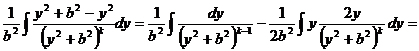
![]() -
- =
= 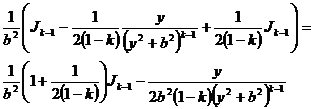
По этой рекуррентной формуле можно последовательно вычислять интегралы ![]() при различных
при различных
![]() , предварительно вычислив
, предварительно вычислив
![]() .
.
Таким образом, показано, что все простейшие рациональные дроби
интегрируемы. Следовательно, класс рациональных функций представляет собой
класс интегрируемых функций.
При интегрировании конкретных рациональных функций выделяют целую часть и раскладывают рациональную дробь на простейшие. Затем
интегрируют простейшие рациональные дроби.
Пример. ![]()
Составляем и решаем систему уравнений относительно неопределенных
коэффициентов (первый способ определения коэффициентов)
 Получим
Получим ![]()
Можно воспользоваться и вторым способом определения коэффициентов.
X=0 | -1 = B-A-C
X=1 | 4 = A+B+2B+C+B-A-C= 4B
X=-1| -2 = A+B-2B-C+B-A-C= -2C. Отсюда C=1, B=1,
A=1.
Вторая система проще, чем первая.
Теперь интегрируем сумму элементарных дробей.
![]()
Оглавление
Интегрирование иррациональностей и тригонометрических функций
1. ![]() , где
, где ![]() – рациональная функция
своих аргументов.
– рациональная функция
своих аргументов.
Такие интегралы всегда можно взять универсальной
тригонометрической подстановкой :
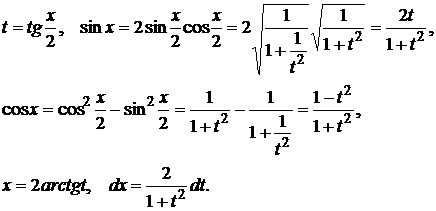
2. ![]() .
.
А) Если ![]() нечетна
по sin x, то делают подстановку t = cos x.
нечетна
по sin x, то делают подстановку t = cos x.
Б) Если ![]() нечетна
по cos x, то делают подстановку t = sin x.
нечетна
по cos x, то делают подстановку t = sin x.
В) Если ![]() не меняет знака при
изменении знака sin x или cos x, то делают подстановку t = tg x.
не меняет знака при
изменении знака sin x или cos x, то делают подстановку t = tg x.
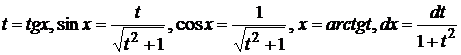
Пример.  . Здесь мы имеем случай В). Подстановкой
. Здесь мы имеем случай В). Подстановкой ![]() этот интеграл сводится
к интегралу
этот интеграл сводится
к интегралу 
 .
.
3. Интегралы ![]()
сводятся к табличным интегралам от
синуса и косинуса, если преобразовать произведение тригонометрических функций в
сумму по формулам
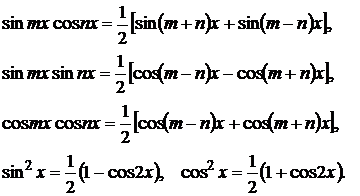
Пример. ![]()
4.
Интегралы
вида ![]()
a) Если m или n – нечетное положительное число, то sin x или cos x вносят под дифференциал.
Пример.![]()
b) Если m, n – четные положительные числа, то
применяют формулы удвоения аргумента ![]()
Пример. ![]()
c) ![]() , где m – целое положительное число, берутся с использованием формул
, где m – целое положительное число, берутся с использованием формул
![]() .
.
Пример. 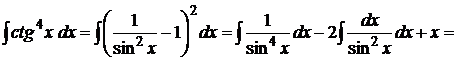
= - ![]()
d) В общем случае интегралы вида ![]() вычисляются по рекуррентным формулам с
использованием основного тригонометрического тождества.
вычисляются по рекуррентным формулам с
использованием основного тригонометрического тождества.
Пример. 
 =
=  .
.
Интегрирование иррациональных
функций.
Рассмотрим интегралы от некоторых иррациональностей,
для которых известны рационализирующие подстановки.
 , где R – рациональная функция аргументов.
Рационализирующая подстановка
, где R – рациональная функция аргументов.
Рационализирующая подстановка ![]() , где
, где ![]() .
.
Не все интегралы могут быть вычислены в элементарных функциях.
Такие интегралы называются неберущимися. Такими
являются, например,  и многие другие
интегралы. Для них составляются специальные таблицы, которые можно найти в
различных учебниках и справочниках.
и многие другие
интегралы. Для них составляются специальные таблицы, которые можно найти в
различных учебниках и справочниках.
Оглавление
Тема 2. Интеграл Римана. Суммы Дарбу
Задача вычисления площади криволинейной трапеции
Рассмотрим криволинейную трапецию, образованную отрезком ![]() осью Oх, прямыми
осью Oх, прямыми ![]() (на
них лежат боковые стороны трапеции) и графиком функции
(на
них лежат боковые стороны трапеции) и графиком функции ![]() .
.
Разобьем произвольным образом отрезок ![]() точками
точками ![]() . Обозначим
. Обозначим ![]() . На каждом отрезке
. На каждом отрезке ![]() отметим точку
отметим точку ![]() . Вычислим
. Вычислим ![]() . Обозначим
. Обозначим ![]() - площадь части
криволинейной трапеции над отрезком
- площадь части
криволинейной трапеции над отрезком ![]() , S – площадь всей криволинейной трапеции. Тогда
, S – площадь всей криволинейной трапеции. Тогда

Пусть функция ![]() непрерывна на каждом
отрезке
непрерывна на каждом
отрезке ![]() . По второй теореме Вейерштрасса выполняется неравенство
. По второй теореме Вейерштрасса выполняется неравенство ![]() , где
, где ![]() - нижняя и верхняя грани функции на отрезке
- нижняя и верхняя грани функции на отрезке ![]() . Тогда
. Тогда

Сумма  называется интегральной суммой, суммы
называется интегральной суммой, суммы  ,
,  называются соответственно нижней и верхней суммами Дарбу.
называются соответственно нижней и верхней суммами Дарбу.
Будем измельчать разбиение так, чтобы ![]() . Если существует
предел интегральных сумм при
. Если существует
предел интегральных сумм при ![]() , то он называется
определенным интегралом (по Риману) от функции
, то он называется
определенным интегралом (по Риману) от функции ![]() по отрезку
по отрезку ![]() :
:  .
.
Если существуют пределы нижней и верхней сумм Дарбу
при ![]() , то они называются нижним
, то они называются нижним ![]() и верхним
и верхним ![]() интегралами Дарбу.
интегралами Дарбу.
Для того,
чтобы существовал определенный интеграл по Риману  , необходимо и достаточно, чтобы существовали и были равны
нижний и верхний интегралы Дарбу.
, необходимо и достаточно, чтобы существовали и были равны
нижний и верхний интегралы Дарбу.
Если определенный интеграл существует
как предел интегральных сумм, то он не зависит
-
от выбора разбиения, лишь бы ![]() ,
,
-
от
выбора точек ![]() на частичных отрезках,
на частичных отрезках,
-
от способа разбиения отрезка, лишь бы
![]() .
.
Поэтому (критерий Римана) для
интегрируемости по Риману ограниченной на отрезке функции необходимо и
достаточно, чтобы существовало некоторое конкретное разбиение отрезка, на
котором ![]() для любого
для любого ![]() .
.
Теорема. Если функция непрерывна на отрезке,
то она интегрируема на этом отрезке.
Теорема. Если функция кусочно непрерывна на
отрезке (имеет на нем не более конечного числа разрывов первого рода), то она
интегрируема на этом отрезке.
От задачи вычисления площади криволинейной трапеции мы пришли к определенному
интегралу. Если функция принимает на отрезке неотрицательные значения, то определенный интеграл можно интерпретировать
как площадь под графиком функции. В этом состоит геометрический смысл определенного интеграла.
К понятию интеграла можно придти и от других задач. К схеме определенного
интеграла сводится любая задача вычисления некоторой величины, аддитивно
зависящей от множества, т.е. величины I, удовлетворяющей соотношению ![]() , где А, В – отрезки оси Oх (в общем случае определенного интеграла
по некоторому множеству А, В – некоторые множества). В качестве таких величин
можно выбрать длину отрезка, длину кривой, площадь поверхности, объем пространственного
тела, массу указанных множеств и т.д.
, где А, В – отрезки оси Oх (в общем случае определенного интеграла
по некоторому множеству А, В – некоторые множества). В качестве таких величин
можно выбрать длину отрезка, длину кривой, площадь поверхности, объем пространственного
тела, массу указанных множеств и т.д.
Оглавление
Тема 3. Свойства интеграла Римана. Теоремы о среднем
Свойства определенного интеграла.
1. Свойство аддитивности (по
множеству)
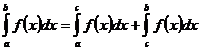
Пусть ![]() . Выберем разбиение так, чтобы точка с
была границей элемента разбиения
. Выберем разбиение так, чтобы точка с
была границей элемента разбиения ![]() . Это возможно (следствие). Составим интегральную сумму
. Это возможно (следствие). Составим интегральную сумму ![]() . Будем измельчать разбиение, сохраняя точку с границей элемента
разбиения. Это возможно (следствие). Тогда предел при
. Будем измельчать разбиение, сохраняя точку с границей элемента
разбиения. Это возможно (следствие). Тогда предел при ![]() левой части равенства интегральных сумм равен
левой части равенства интегральных сумм равен  , первого слагаемого правой части
, первого слагаемого правой части  , второго слагаемого правой части
, второго слагаемого правой части  .
.
2.  .
.
Составляя интегральную сумму для
интеграла в правой части равенства, заметим, что элемент разбиения надо
проходить в другом направлении, от конца отрезка к началу. Поэтому для этого
интеграла интегральная сумма будет ![]() -
- ![]() . Переходя к пределу при измельчении разбиения, получим
. Переходя к пределу при измельчении разбиения, получим  .
.
3.  .
.
4. Если на отрезке ![]() , то
, то  .
.
5. Если на отрезке ![]() , то
, то  .
.
6.  .
.
7.  .
.
8. Пусть на отрезке ![]()
![]() и функция
и функция ![]() интегрируема на
отрезке. Тогда
интегрируема на
отрезке. Тогда 
9. (Первая теорема о среднем) Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() . Тогда существует
. Тогда существует ![]() , что
, что  (или
(или  ).
).
Геометрически, смысл этого соотношения состоит в том, что площадь
криволинейной трапеции равна площади прямоугольника с тем же основанием и
высотой ![]() .
.
Оглавление
Формула Ньютона-Лейбница. Интеграл с переменным верхним пределом
Определенный интеграл представляет собой функцию пределов интегрирования.
Это ясно даже из геометрической интерпретации интеграла как площади
криволинейной трапеции. Изменяя пределы интегрирования, мы изменяем основание
трапеции, изменяя тем самым ее площадь.
Рассмотрим интеграл как функцию верхнего предела интегрирования – интеграл с переменным верхним пределом  . Переменную интегрирования можно заменить другой буквой, например, z или t или какой-либо другой. От этого значение определенного
интеграла не меняется.
. Переменную интегрирования можно заменить другой буквой, например, z или t или какой-либо другой. От этого значение определенного
интеграла не меняется.
Теорема. Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , пусть
, пусть ![]() . Тогда интеграл с переменным верхним пределом является
первообразной этой функции, т.е.
. Тогда интеграл с переменным верхним пределом является
первообразной этой функции, т.е. ![]() для любого
для любого ![]() .
.
Доказательство. 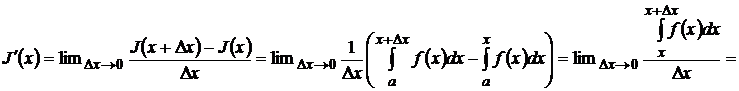
![]() .
.
При доказательстве мы воспользовались теоремой о среднем  и непрерывностью функции
и непрерывностью функции ![]() .
.
Теорема (Формула Ньютона – Лейбница). Пусть
функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() - некоторая
первообразная функции
- некоторая
первообразная функции ![]() . Тогда
. Тогда  .
.
Доказательство. Из теоремы о производной интеграла
по переменному верхнему пределу следует, что ![]() , т.е.
, т.е. ![]() - первообразная для функции
- первообразная для функции ![]() . По теоремам о первообразных две первообразных отличаются на
константу т.е.
. По теоремам о первообразных две первообразных отличаются на
константу т.е. ![]() Но
Но ![]() , поэтому
, поэтому ![]() . Тогда
. Тогда  . Следовательно,
. Следовательно,  .
.
Оглавление
Тема 4. Методы замены переменной и интегрирования по частям
Методы вычисления остаются теми же, что и методы вычисления
неопределенного интеграла, но разница есть. В неопределенном интеграле, делая
замену переменной, надо затем возвратиться к исходной функции, в определенном
интеграле этого делать не нужно, при замене пересчитываются и пределы
интегрирования для новой переменной. Определенный интеграл при постоянных
пределах интегрирования – число и все равно, в каких переменных считать это
число. Но требование взаимной однозначности функции – замены и в определенном
интеграле сохраняется.
Теорема. Пусть
1) ![]() непрерывны при
непрерывны при ![]() ,
,
2) значения ![]() ,
, ![]() не выходят за границы
не выходят за границы ![]() ,
,
3) ![]() ,
,
Тогда 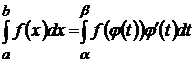
Доказательство.  .
.
Пример  .
.
![]()
Теорема. Пусть
функции ![]() непрерывны на
непрерывны на ![]() . Тогда
. Тогда
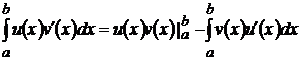
Доказательство остается тем же, что для неопределенного интеграла, только
интегрирование проводится в пределах от a до b.
Интегрирование четных и нечетных функций на отрезке, симметричном относительно
начала координат.
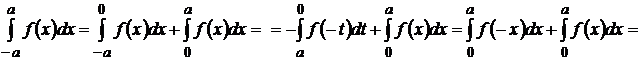
![]()
 , так
как
, так
как  .
.
Интегрирование периодических функций на отрезке длины, кратной периоду.
Если ![]() - периодическая
функция с периодом T, то
- периодическая
функция с периодом T, то  .
.
Доказательство.
 .
.
![]()
![]()
Поэтому интеграл от периодической функции на отрезке, длиной равной
периоду, можно вычислять на любом таком отрезке, результат будет тем же самым.
Заметим, что  . Поэтому, например,
. Поэтому, например,  .
.
Когда встречаются интегралы от
синусов и косинусов на отрезке длины, кратной периоду, то такие интегралы
вычислять не стоит, они равны нулю.
Оглавление
Тема 5. Несобственные интегралы. Признаки сходимости
Пусть отрезок ![]() числовой оси
неограничен. Это возможно в трех случаях:
числовой оси
неограничен. Это возможно в трех случаях: ![]() . Определим несобственные интегралы как пределы
. Определим несобственные интегралы как пределы
 ,
,
 ,
,
 . В последнем интеграле a и b независимо друг от друга стремятся к
. В последнем интеграле a и b независимо друг от друга стремятся к ![]() . Если
. Если ![]() , то предел в правой части последнего равенства называется
главным значением несобственного интеграла.
, то предел в правой части последнего равенства называется
главным значением несобственного интеграла.
Если эти пределы существуют и конечны, то несобственные интегралы
называются сходящимися. Если предел
не существует или бесконечен, то такой несобственный интеграл называется расходящимся.
Если сходятся интегралы от функций ![]() , то сходятся интегралы от функций
, то сходятся интегралы от функций ![]() .
Это следует из теорем о пределах.
.
Это следует из теорем о пределах.
Пример. ![]() , интеграл сходится.
, интеграл сходится.
Пример. ![]() , интеграл расходится.
, интеграл расходится.
Пример. ![]() сходится
при
сходится
при ![]() и расходится при
и расходится при ![]() . Проверьте это.
. Проверьте это.
Рассмотрим интеграл Дирихле ![]() .
.
 .
.
При ![]()
![]() , интеграл расходится.
, интеграл расходится.
Итак, несобственный интеграл
Дирихле первого рода ![]() сходится при
сходится при ![]() расходится при
расходится при ![]()
Признаки сравнения несобственных интегралов (достаточные признаки сходимости и расходимости несобственных
интегралов).
Теорема. Пусть при ![]() выполнено неравенство
выполнено неравенство ![]() .
.
Если интеграл  сходится, то и
интеграл
сходится, то и
интеграл  сходится.
сходится.
Если интеграл  расходится, то и
интеграл
расходится, то и
интеграл  расходится.
расходится.
Доказательство. Проинтегрируем неравенство ![]() на отрезке
на отрезке ![]() ,
,
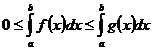 . Так как обе функции на отрезке имеют только положительные
значения, то интегралы от этих функций представляют собой возрастающие функции
от верхнего предела b.
. Так как обе функции на отрезке имеют только положительные
значения, то интегралы от этих функций представляют собой возрастающие функции
от верхнего предела b.
Если  сходится (
сходится ( = I), то при любом b > a
= I), то при любом b > a ![]()
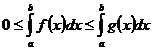
![]()
 = I (I – конечное число).
= I (I – конечное число).
Поэтому  - монотонно возрастающая, ограниченная функция верхнего
предела интегрирования b. Следовательно, по теореме Вейерштрасса этот интеграл как
функция b имеет предел
- монотонно возрастающая, ограниченная функция верхнего
предела интегрирования b. Следовательно, по теореме Вейерштрасса этот интеграл как
функция b имеет предел
 , т.е. интеграл
, т.е. интеграл  сходится.
сходится.
Пусть теперь расходится. Если
расходится. Если  сходится, то по доказанному и
сходится, то по доказанному и  сходится,
противоречие. Теорема доказана.
сходится,
противоречие. Теорема доказана.
Теорема. Пусть при x>a ![]() . Если существует конечный предел
. Если существует конечный предел ![]() , то интегралы
, то интегралы  ,
,  , сходятся или расходятся одновременно (если один сходится,
то и другой сходится, если один расходится, то и другой расходится).
, сходятся или расходятся одновременно (если один сходится,
то и другой сходится, если один расходится, то и другой расходится).
Эталонами служат обычно интегралы Дирихле или интегралы от показательной
функции.
Пример. ![]() сходится
по второму признаку сравнения, интеграл сравнения
сходится
по второму признаку сравнения, интеграл сравнения ![]() .
.
Пример. ![]() сходится
по первому признаку, интеграл сравнения
сходится
по первому признаку, интеграл сравнения
![]() .
.
Несобственные интегралы от разрывной функции по конечному промежутку (второго
рода).
Функция может терпеть разрыв на левом конце отрезка ![]() , на правом конце или в некоторой внутренней точке с отрезка.
, на правом конце или в некоторой внутренней точке с отрезка.
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() за исключением точки x= a, тогда несобственным интегралом
второго рода от функции
за исключением точки x= a, тогда несобственным интегралом
второго рода от функции ![]() по отрезку
по отрезку ![]()
 называется предел
называется предел  =
= .
.
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() за исключением точки x= b, тогда несобственным интегралом
второго рода от функции
за исключением точки x= b, тогда несобственным интегралом
второго рода от функции ![]() по отрезку
по отрезку ![]()
 называется предел
называется предел  =
= .
.
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() за исключением точки x=
за исключением точки x= ![]() ,
тогда несобственным интегралом второго рода от функции
,
тогда несобственным интегралом второго рода от функции ![]() по отрезку
по отрезку ![]() называется
называется  =
= (интегралы в правой части определены выше).
(интегралы в правой части определены выше).
Если указанные пределы существуют и конечны, то интегралы называются сходящимися, если предел бесконечен или
не существует вообще, то интеграл расходится.
Если сходятся интегралы от функций ![]() , то сходятся интегралы от функций
, то сходятся интегралы от функций ![]() .
Это следует из теорем о пределах.
.
Это следует из теорем о пределах.
Пример. 
![]() Интеграл расходится,
так как пределы в правой части равенства бесконечны.
Интеграл расходится,
так как пределы в правой части равенства бесконечны.
Заметим, если здесь формально применить формулу Ньютона-Лейбница (она
неприменима, т.к. функция разрывна), получим ответ 2.
Еще раз убеждаемся, что теоремы следует применять, внимательно проверяя условия
их применимости.
Рассмотрим несобственный интеграл
Дирихле второго рода  .
.
 .
.
При ![]()
 , интеграл расходится.
, интеграл расходится.
Итак, несобственный интеграл
Дирихле второго рода  сходится при
сходится при ![]() расходится при
расходится при ![]()
Замечание. Интегралы Дирихле первого и второго
рода расходятся при n=1. При n>1 интеграл Дирихле первого рода сходится, а интеграл Дирихле второго
рода расходится. При n<1 интеграл Дирихле первого рода расходится, а интеграл
Дирихле второго рода сходится.
Признаки сравнения интегралов остаются верными и для интегралов второго
рода. Эталонами сравнения служат обычно интегралы Дирихле и интегралы от
показательной функции.
Примеры.  сходится сравнением с несобственным интегралом Дирихле
сходится сравнением с несобственным интегралом Дирихле
![]() (n=
(n=![]() ) по второму признаку сравнения. Вспомните, что сумма
бесконечно малых функций в знаменателе эквивалентна при
) по второму признаку сравнения. Вспомните, что сумма
бесконечно малых функций в знаменателе эквивалентна при ![]() бесконечно малой наинизшего порядка малости. Можно доказать эквивалентность
непосредственным вычислением предела.
бесконечно малой наинизшего порядка малости. Можно доказать эквивалентность
непосредственным вычислением предела.
![]() расходится
сравнением с интегралом
расходится
сравнением с интегралом ![]() по второму признаку
сравнения.
по второму признаку
сравнения.
Абсолютная сходимость несобственных интегралов.
До сих пор при анализе сходимости несобственных интегралов мы
предполагали, что подинтегральная функция принимает
только положительные значения. Откажемся от этого предположения. Будем
исследовать сходимость несобственных интегралов первого рода вида  , где
, где ![]() может принимать
значения любого знака. Полученные результаты переносятся по аналогии на остальные
несобственные интегралы первого и второго рода.
может принимать
значения любого знака. Полученные результаты переносятся по аналогии на остальные
несобственные интегралы первого и второго рода.
Интеграл  называется абсолютно
сходящимся, если сходится несобственный интеграл
называется абсолютно
сходящимся, если сходится несобственный интеграл  .
.
Теорема. Если интеграл  абсолютно сходится, то
он сходится.
абсолютно сходится, то
он сходится.
Доказательство. Введем в рассмотрение две вспомогательные функции ![]() . Эти функции принимают только положительные значения. Кроме
того,
. Эти функции принимают только положительные значения. Кроме
того, ![]() . По первому признаку сравнения из абсолютной сходимости
интеграла
. По первому признаку сравнения из абсолютной сходимости
интеграла , т.е. из сходимости интеграла
, т.е. из сходимости интеграла  следует сходимость интегралов
следует сходимость интегралов
 ,
,  . Тогда сходится интеграл
. Тогда сходится интеграл  . Теорема доказана.
. Теорема доказана.
Пример.  абсолютно сходится, так как
абсолютно сходится, так как ![]() а интеграл
а интеграл  сходится.
сходится.
Условная сходимость несобственных интегралов.
Интеграл  называется условно сходящимся, если он сходится, а
интеграл
называется условно сходящимся, если он сходится, а
интеграл  расходится.
расходится.
Покажем, что интеграл  условно сходится.
условно сходится.
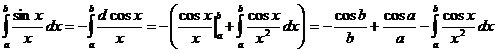
Перейдем к пределу при ![]() . Интеграл в правой части равенства абсолютно сходится,
обозначим его I.
. Интеграл в правой части равенства абсолютно сходится,
обозначим его I.
 . Поэтому интеграл
. Поэтому интеграл  сходится.
сходится.
Покажем, что этот интеграл не сходится абсолютно. Справедливо неравенство
![]() .
.  .
.
Переходя к пределу при ![]() , видим, что интеграл
, видим, что интеграл  сходится (аналогично интегралу
сходится (аналогично интегралу  ), интеграл
), интеграл  расходится. Поэтому
интеграл
расходится. Поэтому
интеграл  расходится. Если бы он
сходился, то складывая его с сходящимся интегралом 0.5
расходится. Если бы он
сходился, то складывая его с сходящимся интегралом 0.5 , получили бы сходящийся интеграл (0.5
, получили бы сходящийся интеграл (0.5![]() ), а этот интеграл расходится.
), а этот интеграл расходится.
Используя неравенство ![]() и расходимость
интеграла
и расходимость
интеграла  , по первому признаку сравнения получаем расходимость
интеграла
, по первому признаку сравнения получаем расходимость
интеграла  . Следовательно, интеграл
. Следовательно, интеграл  условно сходится.
условно сходится.
Оглавление
Тема 6. Двойной интеграл. Свойства. Вычисление
Пусть
функция ![]() определена внутри некоторой области
определена внутри некоторой области ![]() и на ее границе. Разобьем область
и на ее границе. Разобьем область ![]() на
на ![]() частичных областей
частичных областей ![]() .
Их площади обозначим через
.
Их площади обозначим через ![]() .
Наибольшую хорду (отрезок, соединяющий две точки границы области) каждой из
областей назовем ее диаметром. Через
.
Наибольшую хорду (отрезок, соединяющий две точки границы области) каждой из
областей назовем ее диаметром. Через ![]() обозначим
диаметр, наибольший из всех
обозначим
диаметр, наибольший из всех ![]() диаметров. В каждой частичной области возьмем
по точке (
диаметров. В каждой частичной области возьмем
по точке (![]() в области
в области ![]() ,
,
![]() в области
в области ![]() ,
и т.д.). Составим интегральную сумму:
,
и т.д.). Составим интегральную сумму: ![]() .
.
Устремим
![]() к бесконечности так, чтобы
к бесконечности так, чтобы ![]() стремилось к нулю. Конечный предел
последовательности Sn (если он существует) при h → 0 , который не зависит ни от способа разбиения
области D , ни от выбора точек
стремилось к нулю. Конечный предел
последовательности Sn (если он существует) при h → 0 , который не зависит ни от способа разбиения
области D , ни от выбора точек ![]() ,
называется двойным интегралом функции
,
называется двойным интегралом функции ![]() и обозначается
и обозначается
 .
.
Функция
f(x,y) называется
интегрируемой функцией на области D . Область D называется областью
интегрирования.
Непрерывная
на замкнутой области функция является интегрируемой на этой области.
Пусть
интегрируемая функция f(x,y)
принимает в области D только положительные значения. Тогда двойной интеграл
 численно равен объему вертикального цилиндрического тела, построенного на
основании D и ограниченного сверху соответствующим куском поверхности z = f(x,y).
численно равен объему вертикального цилиндрического тела, построенного на
основании D и ограниченного сверху соответствующим куском поверхности z = f(x,y).
Вычисление двойного
интеграла
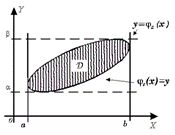
Если
граница области D пересекается всякой прямой x = c (c - const)
не более чем в двух точках, то область D называется правильной в направлении
оси OX. Ограниченная область D , правильная в направлении оси ОХ, задается
неравенствами: a ≤ x ≤ b, φ1(x)
≤ y ≤ φ2(x), где φ1(x),
φ2(x) - функции, непрерывные на
отрезке [a, b] .
В
этом случае двойной интеграл сводится к двукратному интегралу  .
.
Сначала,
полагая переменную интегрирования x постоянной,
находим определенный интеграл  как функцию Ф(x) переменной x Затем находим определенный интеграл
как функцию Ф(x) переменной x Затем находим определенный интеграл
 .
.
Оглавление
Модуль 2. Ряды
Тема 7. Числовые ряды и их свойства
Пусть дана числовая последовательность ![]() . Образуем выражение
. Образуем выражение
 (1)
(1)
которое
называется числовым рядом. Числа ![]() называются членами
ряда, а выражение
называются членами
ряда, а выражение ![]() -
общим членом ряда.
-
общим членом ряда.
Пример
1.
Найти общий член
ряда
 .
.
При
 , при
, при  , при
, при 
Нетрудно
заметить, что общий член
ряда  .
.
Поэтому искомый
ряд можно записать
следующим образом  .
.
Построим
из членов ряда
(1) последовательность таким образом:
![]() ;
;
![]() ;
;
![]() ;
;
…
![]() .
.
Каждый
член этой последовательности представляет собой сумму соответствующего числа первых
членов числового ряда.
Сумма
первых п
членов ряда (1) называется n-ой частичной суммой
числового ряда.
Числовой
ряд  называется сходящимся,
если
называется сходящимся,
если ![]() , где число
, где число ![]() называется суммой ряда, и пишут
называется суммой ряда, и пишут  . Если предел
частичных сумм бесконечен или не существует, то ряд называется расходящимся.
. Если предел
частичных сумм бесконечен или не существует, то ряд называется расходящимся.
Пример
2.
Проверить на сходимость
ряд  .
.
Для
того, чтобы вычислить n-ю частичную сумму ![]() представим общий член
представим общий член  ряда
ряда  в виде суммы простейших
дробей
в виде суммы простейших
дробей
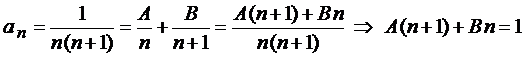
Сравнивая
коэффициенты при одинаковых степенях n, получим систему линейных алгебраических
уравнений относительно неизвестных коэффициентов А
и В 
Отсюда
находим, что ![]() , а
, а ![]() .
.
Следовательно,
общий член ряда
имеет вид 
Тогда
частичную сумму ![]() можно представить в виде
можно представить в виде
 .
.
После
раскрытия скобок и приведения подобных членов, она примет вид  .
.
Вычислим
сумму ряда 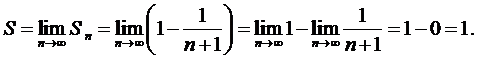
Так
как предел равен
конечному числу, то
данный ряд сходится.
Пример
2.
Проверить на сходимость
ряд ![]() - бесконечную геометрическую прогрессию.
- бесконечную геометрическую прогрессию.
Как
известно, сумма первых
п членов геометрической прогрессии при q ![]() 1 равна
1 равна
 .
.
Тогда
имеем следующие случаи:
1.
Если ![]() , то
, то 
2.
Если ![]() , то
, то ![]() , т.е. ряд расходится.
, т.е. ряд расходится.
3.
Если ![]() , то ряд имеет вид
, то ряд имеет вид ![]() и тогда
и тогда ![]() , т.е. ряд расходится.
, т.е. ряд расходится.
4.
Если ![]() , то ряд имеет вид
, то ряд имеет вид ![]() и тогда
и тогда ![]() , если частичная сумма имеет четное число членов и
, если частичная сумма имеет четное число членов и ![]() , если нечётное число, т.е.
, если нечётное число, т.е. ![]() не существует,
следовательно, ряд расходится.
не существует,
следовательно, ряд расходится.
Разность
между суммой ряда S и частичной суммой ![]() называется остатком ряда и обозначается
называется остатком ряда и обозначается ![]() , т.е.
, т.е.  .
.
Так как для сходящихся рядов ![]() , то
, то ![]() , т.е.
, т.е. ![]() будет б.м.в. при
будет б.м.в. при ![]() . Таким образом, значение
. Таким образом, значение ![]() является приближенным значением суммы ряда.
является приближенным значением суммы ряда.
Из
определения суммы ряда
следуют свойства сходящихся рядов:
1.
Если ряды  и
и  сходятся, т.е. имеют
соответственно суммы S и Q,
то сходится ряд
сходятся, т.е. имеют
соответственно суммы S и Q,
то сходится ряд  , где
, где ![]() , а его сумма
равна A
S
+
B
Q.
, а его сумма
равна A
S
+
B
Q.
2.
Если сходится ряд  , то сходится и ряд,
полученный из данного ряда отбрасыванием
или добавлением конечного числа членов. Верно и обратное.
, то сходится и ряд,
полученный из данного ряда отбрасыванием
или добавлением конечного числа членов. Верно и обратное.
Необходимый признак сходимости. Гармонический ряд
Теорема.
Если ряд ![]() сходится, то общий член ряда стремится к нулю при
сходится, то общий член ряда стремится к нулю при
![]() , т.е.
, т.е. ![]() .
.
Действительно,
имеем ![]() , тогда
, тогда ![]() , что и требовалось
доказать.
, что и требовалось
доказать.
Если
же ![]() , то ряд расходится.
Обратное, вообще говоря, неверно.
, то ряд расходится.
Обратное, вообще говоря, неверно.
Ряд
вида  называется
гармоническим. Для этого ряда выполняется
необходимый признак, так как
называется
гармоническим. Для этого ряда выполняется
необходимый признак, так как  . В то
же время он является
расходящимся. Покажем это:
. В то
же время он является
расходящимся. Покажем это: 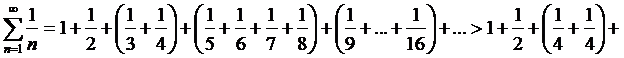
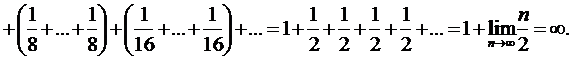
Таким
образом, гармонический ряд расходится.
Оглавление
Тема 8. Сходимость
рядов с неотрицательными членами
Пусть
даны два ряда с положительными
членами:
![]() (1)
(1)
![]() (2)
(2)
Признак
сравнения. Если для всех членов рядов (1) и (2), начиная с
некоторого номера, выполняется неравенство ![]() и ряд (2) сходится, то
сходится и ряд (1). Аналогично, если
и ряд (2) сходится, то
сходится и ряд (1). Аналогично, если ![]() и ряд (2) расходится,
то расходится и ряд (1).
и ряд (2) расходится,
то расходится и ряд (1).
Пусть
![]() и
и ![]() соответственно частичные суммы рядов
(1-2), а Q
-
сумма ряда (2). Тогда
для достаточно больших п имеем
соответственно частичные суммы рядов
(1-2), а Q
-
сумма ряда (2). Тогда
для достаточно больших п имеем ![]() .
.
Так
как ![]() и ограничена, то
и ограничена, то ![]() , т.е. ряд (1)
сходится.
, т.е. ряд (1)
сходится.
Аналогично
доказывается и вторая
часть признака.
Пример 3.
Исследовать на сходимость
ряд  .
.
Сравним
с членами ряда  . Начиная с
. Начиная с ![]() , имеем
, имеем  . Так как
ряд
. Так как
ряд  сходится
сходится  , то данный ряд также
сходится.
, то данный ряд также
сходится.
На
практике часто более удобно пользоваться так называемым предельным признаком сравнения, который вытекает из предыдущего.
Предельный
признак сравнения. Если для двух рядов (1-2) с положительными членами выполняется условие 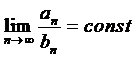
![]() , то
, то
из
сходимости ряда (1) следует сходимость
ряда (2), а из расходимости ряда (1) следует
расходимость ряда (2), т.е. ряды ведут
себя одинаково.
Пример
4.
Исследовать на сходимость
ряд  .
.
В
качестве ряда для
сравнения возьмем гармонический ряд  , который является расходящимся.
, который является расходящимся.
Тогда  а, следовательно, наш ряд
расходится.
а, следовательно, наш ряд
расходится.
Замечание.
Часто для сравнения удобно использовать так называемый обобщённый гармонический
ряд  , который, как будет показано ниже, сходится при
, который, как будет показано ниже, сходится при ![]() и расходится
при
и расходится
при ![]() .
.
Признак Даламбера.
Теорема 1. Пусть для ряда с положительными членами  существует конечный или бесконечный
предел
существует конечный или бесконечный
предел  , тогда:
, тогда:
1. Если ![]() - ряд сходится;
- ряд сходится;
2. Если ![]() - ряд расходится;
- ряд расходится;
3. Если ![]() - ответа на вопрос
о сходимости теорема не даёт.
В
этом случае требуются дополнительные исследования.
- ответа на вопрос
о сходимости теорема не даёт.
В
этом случае требуются дополнительные исследования.
Пример 1.
Исследовать сходимость ряда  .
.
Вычислим предел 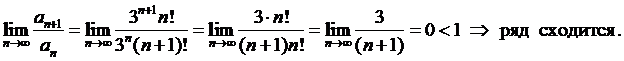
Пример 2.
Исследовать сходимость ряда  .
.
Вычислим предел  , т.е. ряд расходится.
, т.е. ряд расходится.
Признак Коши.
Теорема 2. Пусть для ряда с положительными
членами  существует конечный или бесконечный
предел
существует конечный или бесконечный
предел ![]() , тогда:
, тогда:
1. Если ![]() - ряд
сходится;
- ряд
сходится;
2. Если ![]() - ряд
расходится;
- ряд
расходится;
3. Если ![]() - ответа на
вопрос о сходимости
теорема не даёт.
В этом случае
требуются дополнительные исследования.
- ответа на
вопрос о сходимости
теорема не даёт.
В этом случае
требуются дополнительные исследования.
Пример 3. Исследовать сходимость ряда  .
.
Вычислим предел 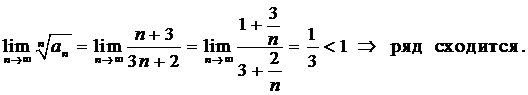
Пример 4. Исследовать сходимость ряда  .
.
Вычислим предел 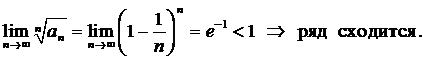
Интегральный признак
Коши.
Пусть дан ряд
с
положительными членами  .
.
Заменим в общем члене
ряда ![]() натуральную переменную
п
вещественной переменной х. Получим
функцию
натуральную переменную
п
вещественной переменной х. Получим
функцию ![]() , для которой
, для которой ![]() . Исходя из геометрического
смысла определённого интеграла, можно доказать
следующую теорему.
. Исходя из геометрического
смысла определённого интеграла, можно доказать
следующую теорему.
Теорема 3. Если функция ![]() непрерывная и
невозрастающая на
непрерывная и
невозрастающая на ![]() , тогда:
, тогда:
1. Если интеграл  сходится, т.е.
сходится, т.е.  , то ряд сходится;
, то ряд сходится;
2. Если интеграл
 расходится, то ряд расходится.
расходится, то ряд расходится.
Пример 5. Исследовать на сходимость
ряд  .
.
Рассмотрим функцию . Для нее имеем
. Для нее имеем 
Таким образом, обобщённый
гармонический ряд сходится, если ![]() и расходится, если
и расходится, если ![]() . Легко убедиться, что признак Даламбера не даёт ответа на вопрос
о сходимости этого ряда.
. Легко убедиться, что признак Даламбера не даёт ответа на вопрос
о сходимости этого ряда.
Оглавление
Тема 9. Знакопеременные
ряды. Их сходимость
Знакочередующиеся
ряды. Теорема Лейбница.
Ряд называется знакопеременным,
если среди его членов имеется бесконечное число как положительных, так и
отрицательных членов.
Знакопеременный ряд, члены
которого имеют чере-дующиеся
знаки, называется знакочередующимся рядом.
Такой ряд имеет
вид ![]() , где все
, где все ![]() .
.
Теорема Лейбница. Если в знакочередующемся ряде члены
ряда удовлетворяют условиям:
1. ![]() ;
;
2. ![]() , то ряд сходится,
и его сумма
не превосходит первого
члена.
, то ряд сходится,
и его сумма
не превосходит первого
члена.
Рассмотрим чётные
частичные суммы такого
ряда
![]() .
.
Все члены в скобках
положительные, следовательно, ![]() и
и ![]() с ростом т.
с ростом т.
Теперь запишем эту сумму
так ![]() .
.
Тогда ![]() , т.е. сумма ограничена сверху и при этом
, т.е. сумма ограничена сверху и при этом ![]() . Тогда по свойству предела она имеет
предел
. Тогда по свойству предела она имеет
предел ![]() , причем
, причем ![]() .
.
Покажем теперь, что и ![]() . Так как
. Так как ![]() , то переходя к пределу
в этом равенстве
получим
, то переходя к пределу
в этом равенстве
получим
![]() , ч.т.д.
, ч.т.д.
Пример 6. Ряд  сходится, так как
удовлетворяет условиям теоремы Лейбница. При этом приближённое вычисление его
суммы будет вычисляться
с точностью
сходится, так как
удовлетворяет условиям теоремы Лейбница. При этом приближённое вычисление его
суммы будет вычисляться
с точностью  .
.
Пример 7. Исследовать сходимость ряда  .
.
Замечаем, что  и тогда по
теореме Лейбница
и тогда по
теореме Лейбница
1.  ; 2.
; 2.  , т.е. ряд сходится.
, т.е. ряд сходится.
Абсолютная и условная
сходимость
Теорема. Если ряд, составленный из абсолютных
величин членов данного ряда, сходится, то сходится и данный ряд. Обратное,
вообще говоря, неверно.
Обозначим суммы
положительных и отрицательных членов частичной суммы соответственно ![]() и
и ![]() . Тогда частичная сумма
данного ряда
. Тогда частичная сумма
данного ряда
![]() , (2)
, (2)
а частичная сумма ряда, образованного
из абсолютных величин членов ряда будет
равна
![]() .
(3)
.
(3)
По условию теоремы
существует предел (3), следовательно, существуют пределы ![]() и
и ![]() .
.
Отсюда следует, что будет
существовать и предел
(2), ч.т.д.
Замечание 2. Обратное не всегда имеет место. Так, в примере 6 ряд сходится, однако
ряд, составленный из положительных величин членов ряда, является расходящимся
как гармонический. В примере 7 ряд сходится, сходится и ряд, составленный из
абсолютных величин членов ряда, в чём легко убедится,
сравнив его с
обобщенным гармоническим ![]() .
.
Определение 3. Знакопеременный ряд называется абсолютно
сходящимся, если сходится ряд, составленный из абсолютных величин его
членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных
величин его членов, расходится, то такой ряд называется условно сходящимся.
Таким образом, в примере 6 ряд является условно
сходящимся, а в примере 7 - ряд абсолютно сходящийся.
Замечание 3. Следует отметить, что разделение
рядов на абсолютно и условно сходящиеся является
существенным, что видно из следующих свойств:
1. Если ряд сходится
абсолютно, то он остаётся абсолютно сходящимся при любой перестановке его
членов. При этом сумма не зависит от порядка его членов.
2. Если ряд сходится
условно, то какое бы не было число А, в том числе и бесконечность, можно переставить члены
этого ряда, чтобы его сумма оказалась равной
А.
3. Если два ряда сходятся
абсолютно, то их произведение - также абсолютно сходящийся ряд, сумма которого равна произведению сумм
этих рядов.
Для условно сходящихся рядов свойство
3 не выполняется.
Оглавление
Тема 10. Степенной
ряд. Функциональные свойства
Степенным рядом называется ряд вида 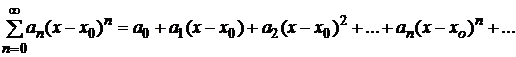
Степенной ряд заведомо сходится при ![]() - центр
сходимости ряда.
- центр
сходимости ряда.
Теорема Абеля. 1) Пусть степенной ряд сходится в
точке ![]() . Тогда он абсолютно сходится в интервале
. Тогда он абсолютно сходится в интервале
![]() , симметричном относительно
, симметричном относительно ![]() .
.
2) Пусть степенной ряд расходится в точке ![]() . Тогда он расходится в области
. Тогда он расходится в области ![]() .
.
Рассмотрим монотонно убывающую последовательность ![]() , такую, что в точке
, такую, что в точке ![]() степенной ряд
степенной ряд  расходится. Если
выбрать
расходится. Если
выбрать ![]() , то степенной ряд будет сходиться (ряд из нулей), поэтому
рассматриваемая последовательность ограничена снизу нулем. По теореме
Вейерштрасса монотонно убывающая, ограниченная снизу числовая последовательность
имеет предел. То есть
, то степенной ряд будет сходиться (ряд из нулей), поэтому
рассматриваемая последовательность ограничена снизу нулем. По теореме
Вейерштрасса монотонно убывающая, ограниченная снизу числовая последовательность
имеет предел. То есть ![]() .
.
Такое число ![]() называется радиусом сходимости степенного ряда.
Следовательно, степенной ряд (по
теореме Абеля) абсолютно сходится в
интервале
называется радиусом сходимости степенного ряда.
Следовательно, степенной ряд (по
теореме Абеля) абсолютно сходится в
интервале ![]() сходимости степенного ряда.
сходимости степенного ряда.
Зафиксируем некоторое значение x и запишем ряд из модулей членов степенного
ряда  . Это – знакоположительный числовой
ряд. Применим к нему признак Даламбера или признак Коши.
. Это – знакоположительный числовой
ряд. Применим к нему признак Даламбера или признак Коши.
Применяя признак Даламбера, имеем
 . Отсюда
. Отсюда  . Поэтому
. Поэтому  .
.
Применяя признак Коши, имеем  .
.
Так определяется радиус сходимости
степенного ряда.
Затем исследуется сходимость ряда на
границе интервала сходимости, в точках ![]() Эти точки
подставляются в исходный ряд, ряд становится обычным числовым рядом и
исследуется стандартными методами для числовых рядов.
Эти точки
подставляются в исходный ряд, ряд становится обычным числовым рядом и
исследуется стандартными методами для числовых рядов.
Пример.  .
.
Составим ряд из модулей  , применим радикальный признак Коши
, применим радикальный признак Коши  .
.
Радиус сходимости R=5, интервал сходимости (-2, 8). Исследуем сходимость ряда на
границе, подставляя точки x= -2, в исходный ряд.
В точке x = -2 имеем ряд  - гармонический ряд, он расходится.
- гармонический ряд, он расходится.
В точке x = 8 имеем ряд  - сходящийся (по признаку Лейбница)
знакочередующийся ряд.
- сходящийся (по признаку Лейбница)
знакочередующийся ряд.
Область сходимости
исходного ряда (-2, 8].
Внутри интервала сходимости справедливы теоремы о непрерывности суммы
ряда, о почленном интегрировании и дифференцировании
ряда.
Теорема. При почленном
дифференцировании и интегрировании степенного ряда его радиус сходимости не
меняется.
Доказательство. Рассмотрим ряд из модулей членов
степенного ряда (это – знакоположительный числовой
ряд в конкретной точке) и определим радиус сходимости по признаку Даламбера.
 .
.
Продифференцируем почленно степенной ряд  , перейдем к ряду из модулей и найдем радиус сходимости по
признаку Даламбера.
, перейдем к ряду из модулей и найдем радиус сходимости по
признаку Даламбера.
 .
.
Таким образом, при почленном дифференцировании
радиус сходимости степенного ряда не меняется. Он не меняется и при почленном интегрировании, иначе он изменился бы при почленном дифференцировании.
Оглавление
Модуль 3. Дифференциальные уравнения
Тема 11. Дифференциальные уравнения первого порядка
Дифференциальным уравнением
называется уравнение относительно независимой переменной, неизвестной функции и ее производных.
Дифференциальное уравнение общего
вида выглядит следующим образом: ![]() . Здесь x – независимая переменная, y(x) – неизвестная функция.
. Здесь x – независимая переменная, y(x) – неизвестная функция.
Порядком дифференциального уравнения
называется порядок старшей производной, входящей в уравнение.
Если, пользуясь теоремой о неявной функции, из уравнения общего вида
удается выразить явно старшую производную, то такое уравнение называется уравнением, разрешенным относительно старшей
производной.
![]() .
.
Дифференциальные уравнения первого порядка.
Дифференциальное уравнение первого порядка общего вида выглядит следующим образом: ![]() .
.
Предположим, что дифференциальное уравнение удалось разрешить
относительно производной: ![]() или
или ![]() .
.
Функция ![]() называется решением дифференциального уравнения первого порядка, если при подстановке
этого решения в уравнение получаем тождество:
называется решением дифференциального уравнения первого порядка, если при подстановке
этого решения в уравнение получаем тождество: ![]() .
.
Функция ![]() называется общим решением дифференциального уравнения первого порядка в области
называется общим решением дифференциального уравнения первого порядка в области ![]() , если
, если
-
при
любой постоянной ![]() функция
функция ![]() является решением,
является решением,
-
для
любого набора начальных условий ![]() существует константа
существует константа ![]() такая, что
такая, что ![]() , т.е. существует решение из семейства
, т.е. существует решение из семейства ![]() (при
(при
![]() ), удовлетворяющее этим начальным условиям.
), удовлетворяющее этим начальным условиям.
Одной из основных задач является
задача отыскания общего решения дифференциального уравнения.
Если зафиксировать постоянную в общем решении,
мы получим частное решение дифференциального
уравнения первого порядка.
Интегральной кривой называется график решения
дифференциального уравнения.
Одной из основных задач является
также задача Коши - задача отыскания частного решения дифференциального уравнения,
удовлетворяющего заданным начальным условиям ![]() или интегральной
кривой, проходящей через заданную точку
или интегральной
кривой, проходящей через заданную точку ![]() .
.
Уравнения с разделяющимися переменными.
Уравнение с разделяющимися переменными имеет вид ![]() .
.
В этом уравнении переменные «можно разделить», т.е. функции от x и dx собрать в правую часть, а функции от
y и dy – в левую часть. Затем интегрируем полученное соотношение и
получаем соотношение вида ![]() .
.
![]() .
.
Пример. ![]() . Заметим, что
. Заметим, что![]() - решение, это так называемое тривиальное решение. Только,
проанализировав, является ли
- решение, это так называемое тривиальное решение. Только,
проанализировав, является ли ![]() решением или нет, мы
имеем право, разделив обе части на
решением или нет, мы
имеем право, разделив обе части на ![]() , двигаться дальше. Иначе тривиальное решение будет потеряно.
, двигаться дальше. Иначе тривиальное решение будет потеряно.
![]() .
.
Здесь нельзя потерять модуль, иначе потеряем решения при
![]() .
.
![]() .
.
Обозначим ![]() и раскроем модуль:
и раскроем модуль:
![]() .
.
Заменим ![]() и разрешим С быть равной нулю, т.к.
тривиальное решение есть. Окончательно,
и разрешим С быть равной нулю, т.к.
тривиальное решение есть. Окончательно, ![]() , где С – произвольная
действительная постоянная.
, где С – произвольная
действительная постоянная.
Пример. Найти кривую, проходящую через точку ![]() , если угловой коэффициент касательной к кривой в три раза
больше углового коэффициента
радиус-вектора в точке касания.
, если угловой коэффициент касательной к кривой в три раза
больше углового коэффициента
радиус-вектора в точке касания.
![]() - решение,
- решение, ![]() . Подставляя начальные условия, получим
. Подставляя начальные условия, получим ![]() .
.
Однородное уравнение.
Правая часть однородного уравнения зависит от отношения ![]() :
: ![]() .
.
Это позволяет заменить отношение новой переменной ![]() или
или ![]() .
.
![]() .
.
Получено уравнение с разделяющимися переменными. Если ![]() , то исходное уравнение уже является уравнением с
разделяющимися переменными.
, то исходное уравнение уже является уравнением с
разделяющимися переменными.
Пример. ![]() .
. ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() .
.
Линейное уравнение.
Линейное уравнение первого порядка
имеет вид: ![]() .
.
Существует два метода решения линейного уравнения: метод вариации
произвольной постоянной и метод подстановки.
Метод вариации произвольной постоянной будет встречаться нам часто: при
решении неоднородных линейных уравнений высшего порядка, при решении
неоднородных систем линейных уравнений. Его надо знать твердо.
При решении методом вариации
произвольной постоянной сначала решают однородное уравнение (с нулевой
правой частью)
![]()
Это – уравнение с разделяющимися переменными.
![]() .
.
Затем варьируют произвольную
постоянную, полагая ![]() .
.
![]() .
.
Подставляем в неоднородное уравнение:
![]() .
.
При вариации произвольной постоянной здесь обязательно должны сократиться
два члена, в этом идея метода.
![]() , где С – произвольная постоянная.
, где С – произвольная постоянная.
![]() .
.
Видно, что общее решение неоднородного уравнения равно сумме общего
решения однородного уравнения и частного решения неоднородного уравнения. Это
справедливо не только для линейных уравнений первого порядка, но и для линейных
уравнений высших порядков, и для линейных систем. Там подобное утверждение
называется теоремой о структуре общего решения неоднородного уравнения или
системы.
Замечание. Решая уравнение методом вариации,
обязательно приводите его к виду ![]() (если при
(если при ![]() стоит коэффициент, то делить на него обязательно), иначе
метод вариации даст ошибку.
стоит коэффициент, то делить на него обязательно), иначе
метод вариации даст ошибку.
При решении методом подстановки полагают
![]() . Мы видели выше, что решение действительно является
произведением двух функций от x. Этот факт здесь и используется.
. Мы видели выше, что решение действительно является
произведением двух функций от x. Этот факт здесь и используется.
![]() . Подставляем в
уравнение:
. Подставляем в
уравнение: ![]() .
.
Теперь решают либо уравнение ![]() , определяя отсюда
, определяя отсюда ![]() , либо уравнение
, либо уравнение ![]() , определяя отсюда
, определяя отсюда ![]() . Здесь при
интегрировании не надо добавлять константу, она появится позже, при отыскании
второй функции. В первом случае,
остается найти v из
. Здесь при
интегрировании не надо добавлять константу, она появится позже, при отыскании
второй функции. В первом случае,
остается найти v из ![]() .
.
Теперь ![]() =
=![]() , как и выше.
, как и выше.
Во втором случае остается найти u из ![]() ,
, ![]() .
.
Теперь ![]() =
=![]() , как и выше.
, как и выше.
Пример. ![]() .
.
Решение методом вариации. Приводим уравнение, деля на
коэффициент при ![]() :
:
![]() .
.
Решаем однородное уравнение ![]() . Варьируем произвольную постоянную
. Варьируем произвольную постоянную ![]() . Подставляем в неоднородное уравнение
. Подставляем в неоднородное уравнение ![]()
![]() .
.
Решение методом подстановки.
![]() ,
, ![]() ,
,
![]() .
.
Оглавление
Тема 12. Линейные дифференциальные уравнения с постоянными коэффициентами
Линейное однородное дифференциальное
уравнение с постоянными коэффициентами второго порядка имеет вид:
![]() .
.
Будем искать его решение в виде ![]() . Подставляя
. Подставляя ![]() в дифференциальное
уравнение, получим
в дифференциальное
уравнение, получим ![]() Так как
Так как ![]() то имеем
то имеем ![]() - характеристическое уравнение. Решая его, получим корни
- характеристическое уравнение. Решая его, получим корни  .
.
Возможно три случая:
1) ![]() действительны и различны,
действительны и различны,
2) ![]() - комплексно
сопряженные корни,
- комплексно
сопряженные корни,
3) ![]() - действительный
кратный корень.
- действительный
кратный корень.
В случае действительных, различных
корней получаем решения ![]() .
.
Для того, чтобы доказать, что решения составляют фундаментальную систему
решений и общее решение записывается в
виде ![]() ,
,
надо проверить линейную независимость ![]() . Составим определитель Вронского
. Составим определитель Вронского  , так как
, так как ![]() .
.
Заметим, что для уравнения второго порядка проверять линейную
независимость можно проще. Надо показать, что ![]() . Тогда столбцы определителя Вронского линейно независимы и
. Тогда столбцы определителя Вронского линейно независимы и ![]() . В нашем случае
. В нашем случае ![]() при
при ![]() .
.
В случае комплексно сопряженных
корней ![]() , применяя формулу Эйлера
, применяя формулу Эйлера ![]() получим комплексно сопряженные решения
получим комплексно сопряженные решения ![]() . Так как линейная комбинация решений линейного однородного
уравнения тоже является решением, то
. Так как линейная комбинация решений линейного однородного
уравнения тоже является решением, то ![]() являются решениями.
Они линейно независимы, так как
являются решениями.
Они линейно независимы, так как ![]() .
.
Следовательно, общее решение
линейного дифференциального уравнения с постоянными коэффициентами в случае
комплексных корней можно записать по формуле
![]() .
.
В случае кратного действительного
корня ![]() одно из решений
можно выбрать в форме
одно из решений
можно выбрать в форме ![]() .
.
Второе решение будем выбирать в виде ![]() . Подставим в дифференциальное уравнение, чтобы определить
. Подставим в дифференциальное уравнение, чтобы определить ![]() .
.
![]()
![]() ,
,
![]()
Так как ![]() - корень
характеристического уравнения, то
- корень
характеристического уравнения, то ![]() . Так как
. Так как ![]() еще и кратный корень,
то по теореме Виета
еще и кратный корень,
то по теореме Виета ![]() . Поэтому
. Поэтому ![]() . Для определения
. Для определения ![]() имеем уравнение
имеем уравнение ![]() , отсюда
, отсюда ![]() . Выберем
. Выберем ![]() , получим
, получим ![]() .
.
Следовательно, ![]() . Решения
. Решения ![]() линейно независимы, так как
линейно независимы, так как ![]() .
.
Поэтому общее решение линейного
дифференциального уравнения с постоянными коэффициентами в случае кратного
корня можно записать по формуле
![]() .
.
Примеры. 1)![]()
2)![]()
3)![]()
4)![]()
![]() .
.
5)![]()
![]() .
.
Линейное неоднородное
дифференциальное уравнение с постоянными коэффициентами второго порядка имеет
вид: ![]() .
.
1) Пусть правая часть имеет вид ![]() .
.
Ищем частное решение в виде ![]() . Здесь
. Здесь ![]() - полином n-ой степени,
- полином n-ой степени, ![]() - полином, степень которого надо определить.
- полином, степень которого надо определить.
![]() ,
, ![]() .
.
![]()
а) Если ![]() - не корень
характеристического уравнения, то
- не корень
характеристического уравнения, то ![]() , и многочлен
, и многочлен ![]() надо выбирать той же
степени, что и
надо выбирать той же
степени, что и ![]() , т.е. степени n.
, т.е. степени n.
б) Если ![]() - простой корень
характеристического уравнения, то
- простой корень
характеристического уравнения, то ![]() . В этом случае многочлен
. В этом случае многочлен ![]() надо выбирать той же
степени, что и
надо выбирать той же
степени, что и ![]() , т.е. степени n. Тогда степень многочлена надо выбирать равной
n+1. Однако при
дифференцировании
, т.е. степени n. Тогда степень многочлена надо выбирать равной
n+1. Однако при
дифференцировании ![]() производная свободного
члена (постоянной) равна нулю, поэтому
производная свободного
члена (постоянной) равна нулю, поэтому ![]() можно выбирать в виде
можно выбирать в виде ![]() =
=![]() .
.
в) Если ![]() - кратный корень
характеристического уравнения, то
- кратный корень
характеристического уравнения, то ![]() . В этом случае многочлен
. В этом случае многочлен ![]() надо выбирать той же
степени, что и
надо выбирать той же
степени, что и ![]() , т.е. степени n. Тогда степень многочлена
, т.е. степени n. Тогда степень многочлена ![]() надо выбирать равной n+2. Однако при двукратном дифференцировании
надо выбирать равной n+2. Однако при двукратном дифференцировании ![]() производная не только
свободного члена равна нулю, но и
производная линейного члена равна нулю. Поэтому
производная не только
свободного члена равна нулю, но и
производная линейного члена равна нулю. Поэтому
![]() можно выбирать в виде
можно выбирать в виде ![]() =
=![]() .
.
Пример. ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() - не корень
характеристического уравнения, поэтому частное решение надо искать в том же
виде, что и правая часть,
- не корень
характеристического уравнения, поэтому частное решение надо искать в том же
виде, что и правая часть, ![]() . Подставляем в неоднородное уравнение с правой частью
. Подставляем в неоднородное уравнение с правой частью ![]() .
.
![]()
![]() .
.
![]() . Корень
. Корень ![]() содержится один раз
среди корней характеристического уравнения, поэтому частное решение ищется в
виде
содержится один раз
среди корней характеристического уравнения, поэтому частное решение ищется в
виде ![]() .
.
Подставляем в неоднородное уравнение с правой частью ![]() .
.
![]() ,
, ![]() .
.
Суммируя оба частных решения, получаем частное решение неоднородного
уравнения для исходной правой части: ![]() .
.
Общее решение неоднородного уравнения будет ![]() .
.
2) Правая часть имеет вид ![]()
a) Если ![]() не корни
характеристического уравнения, то частное решение ищется в том виде, в котором задана правая
часть:
не корни
характеристического уравнения, то частное решение ищется в том виде, в котором задана правая
часть: ![]() , где
, где ![]() - полиномы степени m – максимальной из степеней полиномов
- полиномы степени m – максимальной из степеней полиномов
![]() .
.
б)
Если ![]() - пара корней характеристического уравнения, то частное
решение ищется в виде
- пара корней характеристического уравнения, то частное
решение ищется в виде ![]() .
.
Пример. ![]()
![]()
![]()
![]()
Пара корней ![]() =
=![]() - пара корней характеристического уравнения.
- пара корней характеристического уравнения.
![]() ,
, 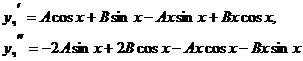
Подставляем в неоднородное уравнение,
получаем ![]() , откуда
, откуда ![]() ,
, ![]() ,
, ![]() .
.
Оглавление
Тема 13. Приложения интегралов, рядов и дифференциальных уравнений
1. Если функция ![]() принимает только
неотрицательные значения, то площадь
принимает только
неотрицательные значения, то площадь ![]() под графиком функции на отрезке [a, b] может быть вычислена с помощью
определенного интеграла
под графиком функции на отрезке [a, b] может быть вычислена с помощью
определенного интеграла  .
.
Но функция может на некотором отрезке принимать и отрицательные значения,
тогда интеграл по этому отрезку будет давать отрицательную площадь, что
противоречит определению площади.
Можно вычислять площадь по формуле S= .
Это равносильно изменению знака функции в тех областях, в которых она принимает
отрицательные значения.
.
Это равносильно изменению знака функции в тех областях, в которых она принимает
отрицательные значения.
Если надо вычислить площадь фигуры, ограниченной сверху графиком функции ![]() , а снизу графиком функции
, а снизу графиком функции ![]() , то можно пользоваться
формулой
, то можно пользоваться
формулой
S= ,
так как
,
так как ![]() .
.
Пример. Вычислить площадь фигуры, ограниченной прямыми x=0, x=2 и графиками функций y=x2, y=x3.
Заметим, что на интервале (0,1) выполнено неравенство x2 > x3, а при x >1 выполнено неравенство x3 > x2. Поэтому
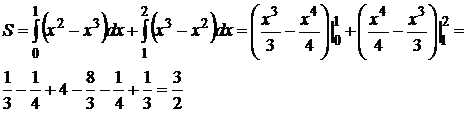
2. Пусть требуется вычислить объем
некоторого тела V по
известным площадям сечений ![]() этого тела
плоскостями, перпендикулярными прямой Oх, проведенными через любую точку x отрезка [a, b] прямой Oх.
этого тела
плоскостями, перпендикулярными прямой Oх, проведенными через любую точку x отрезка [a, b] прямой Oх.
Считая элементарный объем ![]() , над отрезком
, над отрезком ![]() объемом прямого
кругового цилиндра с площадью основания
объемом прямого
кругового цилиндра с площадью основания ![]() и высотой
и высотой ![]() , получим
, получим ![]() . Интегрируя и применяя формулу Ньютона – Лейбница, получим
. Интегрируя и применяя формулу Ньютона – Лейбница, получим  .
.
Пусть требуется вычислить объем
тела вращения вокруг оси Oх.
Тогда  .
.
Аналогично, объем тела вращения
вокруг оси Oу, если
функция задана в виде ![]() , можно вычислить по формуле
, можно вычислить по формуле  .
.
Пример. Вычислить объем шара ![]() .
. 
Пример. Вычислить объем прямого кругового конуса, ограниченного
поверхностью  и плоскостью
и плоскостью ![]() .
.
Вычислим объем, как объем тела вращения, образованного вращением вокруг
оси Oz прямоугольного
треугольника в плоскости Oxz, катеты которого лежат на оси Oz и прямой z = H , а
гипотенуза лежит на прямой ![]() .
.
Выражая x через z, получим  .
.
Искомый объем можно посчитать как разность объемов прямого кругового
цилиндра ![]() с высотой H и тела, вращения, ограниченного
цилиндрической, конической поверхностями
и плоскостью Oxz
с высотой H и тела, вращения, ограниченного
цилиндрической, конической поверхностями
и плоскостью Oxz
 .
.
3. Если дуга представляет собой график непрерывно дифференцируемой функции ![]() ,
дифференциал длины дуги можно вычислить по формуле
,
дифференциал длины дуги можно вычислить по формуле
![]() . Поэтому
. Поэтому 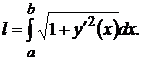
Если гладкая дуга задана параметрически  , то
, то ![]() . Поэтому
. Поэтому  .
.
Пример. Вычислить длину дуги графика функции![]() ,
,  .
. ![]()
 .
.
Пример. Вычислить длину одной арки циклоиды.  .
.
![]() ,
,  .
.
4. Пусть гладкая дуга представляет собой
график непрерывно дифференцируемой функции ![]() . Эта дуга вращается вокруг оси Oх, описывая некоторую поверхность. Площадь этой поверхности вычисляется по
формуле
. Эта дуга вращается вокруг оси Oх, описывая некоторую поверхность. Площадь этой поверхности вычисляется по
формуле  .
.
Оглавление
Литература
1. Фихтенгольц Г.М. Основы математического анализа. Т. 1,
2. М.: Наука, 1968.
2. Шипачев В.С. Задачник по высшей математике. М.: Высшая школа, 2009.
3. Шипачев В.С. Высшая
математика. М.: Юрайт, 2013.
4. Берман Г.Н. Сборник задач по курсу математического
анализа. СПб.: Профессия, 2001.
5. Фихтенгольц Г.М. Курс дифференциального и
интегрального исчисления. Т. 1 –3. ИД:
Лань, 2009.
6. Кудрявцев Л.Д. Курс математического анализа.Т. 1, 2.М.: Высшая школа,
1981.
7. Никольский С.М. Курс
математического анализа.Т.
1, 2. М.: Наука, 1983.
8. Ильин В.А., Позняк Э.Г. Основы математического
анализа. Ч. 1, 2. М.: Наука, 1967.
9. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу.
Интегралы и ряды. М.: Наука, 1986.
10. Камынин
Л.И. Курс математического анализа.Т.
1, 2. М.: Изд. МГУ, 1995.
11. Архипов Г.И., Садовничий В.А., Чубариков В.Н.
Лекции по математическому анализу.
М., 1999.