Заданы некоторые экономические показатели предприятий Комитета по виноградарству, производству и обороту алкогольной и спиртосодержащей продукции РД в 2016 году (см таблицу 1).

Таблица 1

Выручка от реализации продукции и затраты на основное производство предприятий Комитета по виноградарству, производству и обороту алкогольной и спиртосодержащей продукции РД за 2016 г., тыс. руб.

ГУП	Выручка от реализации продукции	Затраты на основное производство
Комсомольское	26841	35559
Башликент	14542	16210
Утамышский	18911	31216
Кр.Окт	50399	79045
Усемикентский	12293	22665
К.Маркса	938	1218
Чкаловский	6648	10601
Буйнакский	6315	7869
Кировский»	63176	63425
Каякентский	59120	111474
Гергинский	11877	12025
Каспий	73907	82244

Выбрать в качестве результативного показателя выручку от реализации продукции, в качестве показателя-фактора – затраты на основное производство.

1. Оценить параметры () парной зависимости выручки от реализации продукции от затрат на основное производство по формулам:

(1).

Результаты расчета параметров и статистических характеристик парной зависимости выручки от реализации продукции от затрат на основное производство представить в таблице 2.

Таблица 2

Обозначения параметров и основных статистических характеристик, необходимых рассчитать

1	10		19
2	11		20
3	12		21
4	13		22
5	14		23
6	15		24
7	16		25
8	17	Δ_a	26
9	18	Δ_b	27

Создать расчетную таблицу в EXCEL, аналогичную таблице 3. Для расчета параметров по формулам (1) использовать столбцы 3-6 таблицы 3, а также средние и суммы по столбцам. Тогда в строках 1и 2 таблицы можно дать ссылки (на соответствующие столбцы таблицы 3) по формулам (1).

Таблица 3

Расчетная таблица для вычисления параметров и основных статистических характеристик линейной регрессии

№ n/n	ГУП
1	2	3	4	5	6	7	8	9
1	Комсомольское	26841	35559
2	Башликент	14542	16210
3	Утамышский	18911	31216
4	Кр.Окт	50399	79045
5	Усемикентский	12293	22665
6	К.Маркса	938	1218
7	Чкаловский	6648	10601
8	Буйнакский	6315	7869
9	Кировский»	63176	63425
10	Каякентский	59120	111474
11	Гергинский	11877	12025
12	Каспий	73907	82244
	Cумма
	Сред. арифметич.

Продолжение

№ n/n
1	10	11	12	13
1
2
…	…	…	…	…
12
Cумма
Сред. арифметич.

2. Оценить тесноту связи изучаемых явлений с помощью линейного коэффициент парной корреляции , для линейной регрессии :

(2), где

, (3).

Для этого добавить столбцы 7 и 8 таблицы 3.

3. Рассчитать индекс корреляции для нелинейной регрессии

(4),

где – расчетные значения результативного показателя (рассчитывается путем подстановки в линейную модель расчетных значений параметров в столбце 9 таблицы 3). Кроме того, добавляются столбцы 10 и 11 в расчетной таблице и определяются их суммарные значения.

4. Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:

(5).

Для расчета средней ошибки аппроксимации необходимо добавить столбец 12 в таблицу 3, рассчитать суммарное значение по этому столбцу, результат умножить на 100 и разделить на количество наблюдений. Результат представить в строке 7 таблицы 2. Допустимый предел значений - не более 8 - 10%.

5. Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора на 1% от своего среднего значения:

(6).

6. Рассчитать коэффициент (индекс) детерминации R²

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

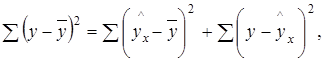
где - общая сумма квадратов отклонений;

- сумма квадратов отклонений, обусловленная регрессией

(«объясненная» или «факторная»);

- остаточная сумма квадратов отклонений.

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R²:

(7).

Коэффициент детерминации - квадрат коэффициента или индекса корреляции.

Для его расчета добавить столбец 13 в таблице 3, определить его суммарное значение. Результат представить в строке 9 таблицы 2, используя ссылки на суммарные значения столбцов 13 и 11 таблицы 3.

7. Оценить статистическую значимость построенной модели, рассчитав значение F-критерия Фишера.

F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н_о о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факг и критического (табличного) F_табл значений F-критерия Фишера. F_фактопределяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

(8), где

п — число единиц совокупности;

- число параметров при переменных .

F_табл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.

Если F_табл< F_факг, то H_о - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл> F_факг, то гипотеза H_о не отклоняется и признается статистическая не значимость, ненадежность уравнения регрессии.

8. Оценить статистическую значимость коэффициентов регрессии и корреляции. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

(9)

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

(10);

(11);

(12)

Сравнивая фактическое и критическое (табличное) значения t-статистики – t-_табл и t_факг - принимаем или отвергаем гипотезу H_о

Связь между F-критерием Фишера и f-статистикой Стьюдента выражается равенством

Если t_табл < t_факг, то Но отклоняется, т.е. a, b и r_xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t_табл > t_факт. то гипотеза Но не отклоняется и признается случайная природа формирования а, b или r_xy

Для расчета доверительного интервала определяем предельную ошибку Δ для каждого показателя:

Δ_a=t_таблm_а, Δ_b=t_таблm_b(13)

Формулы для расчета доверительных интервалов имеют следующий вид:

(14)

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение y_p определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза

(15)

где (16)

и строится доверительный интервал прогноза:

где (17)

Лабораторная работа № 2 по дисциплине «Эконометрика»

Модуль 1. Методы и модели парной регрессии и корреляции

Тема 2. Парная регрессия и корреляция в эконометрических исследованиях

Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии . Порядок вычисления следующий:

1. введите исходные данные из лабораторной работы 1;

2. выделите область пустых ячеек 5х2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1х2 - для получения только оценок коэффициентов регрессии;

3. активизируйте Мастер функций любым из способов:

а) в главном меню выберите Вставка/Функция;

б) на панели инструментов Стандартная щелкните по кнопке Вставка/Функция;

4. в окне Категория (рис. 1.1) выберите Статистические, в окне Функция - ЛИНЕЙН. Щелкните по кнопке ОК;

5. заполните аргументы функции (рис. 1.2):

Рис. 1. Диалоговое окно «Мастер функций»

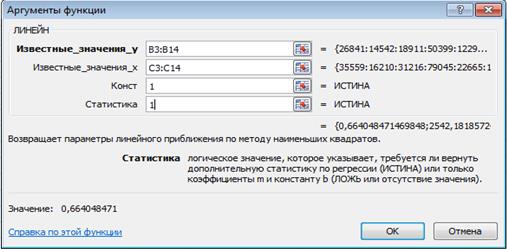
Рис. 2. Диалоговое окно ввода аргументов функции ЛИНЕЙН

Известные_значения_у - диапазон, содержащий данные результативного признака;

Известные_значения_х - диапазон, содержащий данные факторов независимого признака;

Константа - логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;

Статистика - логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

6. в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем - на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента а
Среднеквадратическое отклонение b	Среднеквадратическое отклонение а
Коэффициент детерминации R²	Среднеквадратическое отклонение у
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Для вычисления параметров экспоненциальной кривой y=α×β^x в MS Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.

Для данных из лабораторной работы 1-3 результаты вычисления функций ЛИНЕЙН и ЛГРФПРИБЛ представлены на рис.3.

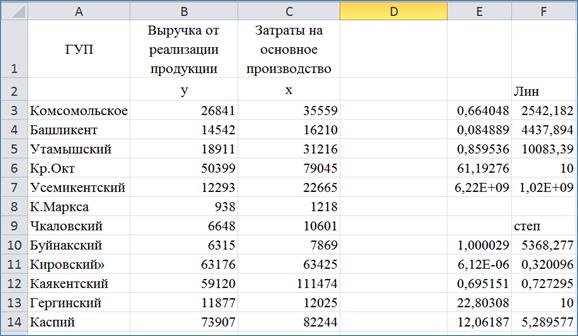
Рис. 3. Результаты вычисления функций ЛИНЕЙН и ЛГРФПРИБЛ

С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1) в главном меню выберите Данные/Анализ данных/Регрессия.

2) заполните диалоговое окно ввода данных и параметров вывода (рис. 4).

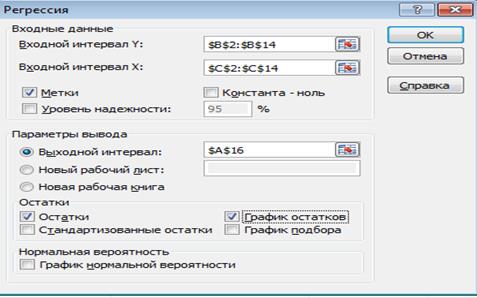
Рис. 4. Диалоговое окно ввода параметров инструмента Регрессия

Входной интервал Y - диапазон, содержащий данные результативного признака;

Входной интервал Х - диапазон, содержащий данные факторов независимого признака;

Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа - ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист - можно задать произвольное имя нового листа.

Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне.

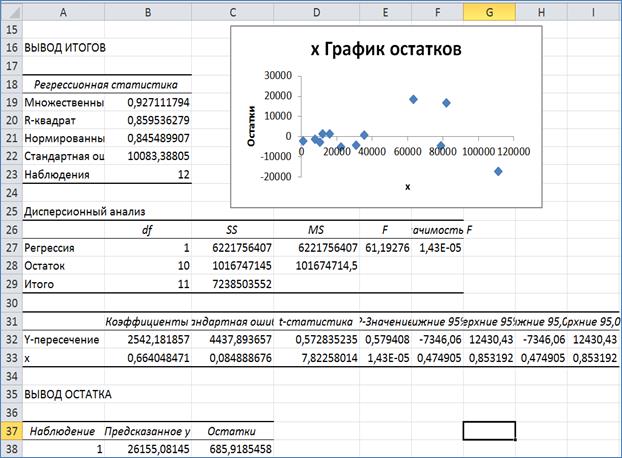
Рис. 5. Результат применения инструмента Регрессия

Лабораторная работа № 3 по дисциплине «Эконометрика»

Модуль 1. Методы и модели парной регрессии и корреляции

Тема 3. Нелинейная регрессия в экономике и ее линеаризация

Заданы некоторые социально-экономические характеристики Центрального ФО РФ в разрезе регионов за 2015 год.

Таблица 1

Некоторые социально-экономические показатели ЦФО РФ за 2015 год

регион	ВРП, млрд. руб.	Инвестиции, млн. руб.
Белгородская обл.	619,4	146,4
Брянская область	243	61,7
Владимирская обл.	327,9	80,5
Воронежская область	709,1	263,6
Ивановская область	151,1	25,7
Калужская область	324,9	92,5
Костромская область	146,3	26,2
Курская область	297,4	70,4
Липецкая область	395,7	116,6
Московская область	2705,6	640,3
Орловская область	179,8	52,3
Рязанская область	297,3	54,1
Смоленская область	234,7	59,9
Тамбовская область	275,8	122,5
Тверская область	307,4	74,2
Тульская область	408,5	105,6
Ярославская область	388,1	69,1
г. Москва	12808,6	1611,5

Требуется построить уравнения зависимости ВРП от инвестиций каждого из следующих видов: линейного, показательного, степенного, гиперболического, параболического. Для этого необходимо составить таблицу 2.

Таблица 2

Расчетная таблица для построения моделей различных видов зависимости ВРП () от объема инвестиций () по данным регионов ЦФО за 2015 г.

№ региона n/n
1	619,4	146,4	6,43	4,99	0,007	146,4	21433,0
2	243	61,7	5,49	4,12	0,016	61,7	3806,9
3	327,9	80,5	5,79	4,39	0,012	80,5	6480,3
4	709,1	263,6	6,56	5,57	0,004	263,6	69485,0
5	151,1	25,7	5,02	3,25	0,039	25,7	660,5
6	324,9	92,5	5,78	4,53	0,011	92,5	8556,3
7	146,3	26,2	4,99	3,27	0,038	26,2	686,4
8	297,4	70,4	5,70	4,25	0,014	70,4	4956,2
9	395,7	116,6	5,98	4,76	0,009	116,6	13595,6
10	2705,6	640,3	7,90	6,46	0,002	640,3	409984,1
11	179,8	52,3	5,19	3,96	0,019	52,3	2735,3
12	297,3	54,1	5,69	3,99	0,018	54,1	2926,8
13	234,7	59,9	5,46	4,09	0,017	59,9	3588,0
14	275,8	122,5	5,62	4,81	0,008	122,5	15006,3
15	307,4	74,2	5,73	4,31	0,013	74,2	5505,6
16	408,5	105,6	6,01	4,66	0,009	105,6	11151,4
17	388,1	69,1	5,96	4,24	0,014	69,1	4774,8
18	12808,6	1611,5	9,46	7,38	0,001	1611,5	2596932,3

Параметры линейной модели оцениваются с помощью встроенной функции ЛИНЕЙН MS EXCEL, а показательного вида – ЛГРФПРИБЛ. Остальные модели сводятся к линейному виду посредством логарифмизации или введения замены. Результаты построения эконометрических моделей различных видов представлены на рис.1.

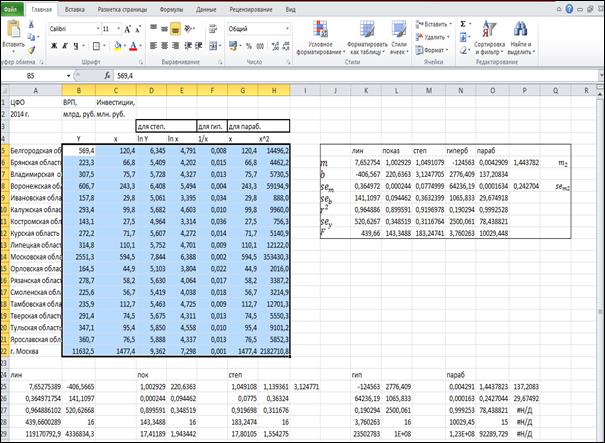
Рис. 4. Результаты построения эконометрических моделей различных видов

Результаты выполнения задания 2 привести в виде следующей таблицы 3.

Таблица 3

Параметры и статистические характеристики эконометрических моделей различных видов

лин	показ	степ	гиперб	параб

В таблице 3 – стандартное значение ошибки для параметра ,
- стандартное значение ошибки для постоянной ,
- коэффициент детерминированности, – стандартная ошибка для оценки , – F-критерий Фишера, – средняя ошибка аппроксимации.

По результатам сделать выводы о характере зависимости ВРП от инвестиций при выборе каждого из построенных видов эконометрических моделей.

Лабораторная работа № 4 по дисциплине «Эконометрика»

Модуль 2. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ

Тема 4. Построение уравнений множественной регрессии, оценка их параметров и характеристик

1. Оценка параметров уравнения множественной регрессии в матричной форме

Заданы некоторые социально-экономические показатели регионов Центрального ФО РФ за 2016 год.

Таблица 1

Некоторые социально-экономические показатели ЦФО РФ за 2016 год

регион	ВРП, млрд. руб.	ОФ, млрд. руб.	Инвестиции, млрд. руб.	Ср. год. числ. занятых в эк., тыс. чел.	СФР, млрд. руб.
Белгородская обл.	686,4	1400,8	143,8	756,8	216,1
Брянская область	269,9	733,1	68,3	540,6	16,1
Владимирская обл.	357,9	787,5	78,5	647,4	36,6
Воронежская область	823,1	1534,6	271,0	1094,8	37,1
Ивановская область	171,0	553,3	22,6	447,1	-0,2
Калужская область	334,8	912,7	80,1	508,9	24,1
Костромская область	157,7	419,5	26,5	293,2	13,6
Курская область	335,3	805,0	89,7	520,6	49,8
Липецкая область	457,6	1179,0	128,0	565,5	43,3
Московская область	3213,9	7237,9	634,7	3377,0	580,0
Орловская область	205,8	472,2	47,9	330,2	15,1
Рязанская область	316,1	927,2	51,1	505,5	33,4
Смоленская область	257,1	829,4	59,9	443,9	16,9
Тамбовская область	344,9	798,3	106,8	492,1	20,5
Тверская область	341,2	1212,7	89,6	608,5	9,0
Тульская область	476,6	1033,1	112,6	731,5	66,8
Ярославская область	432,0	1226,2	81,9	626,6	22,0
г. Москва	13532,6	36338,1	1703,1	8692,0	4649,3

Требуется построить линейное уравнение зависимости ВРП от среднегодовой стоимости основных фондов, инвестиций и среднегодовой численности занятых в экономике.

Методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения множественной регрессии:

. (1)

Здесь - вектор зависимой переменной размерности , представляющий собой наблюдений значений , - матрица независимых переменных, элементы которой наблюдения значений независимых переменных Х₁ X₂, Х₃, ..., Х_m; - подлежащий оцениванию вектор неизвестных параметров размерности ; ε - вектор случайных отклонений (возмущений) размерности . Таким образом,

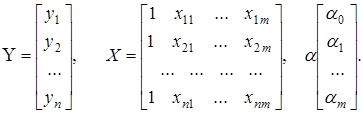
Уравнение (1) содержит значения неизвестных параметров . Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Оценить их по формуле:

Α=(X^TX)^-1X^TY (2)

Лабораторная работа № 5 по дисциплине «Эконометрика»

Модуль 2. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ

Тема 4. Построение уравнений множественной регрессии, оценка их параметров и характеристик

2. Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции

Выбор факторов, влияющих на исследуемый показатель, производится, прежде всего, исходя из содержательного экономического анализа. Для получения надежных оценок в модель не следует включать слишком много факторов. Их число не должно превышать одной трети объема имеющихся данных. Для определения наиболее существенных факторов могут быть использованы коэффициенты линейной и множественной корреляции, детерминации частных коэффициентов корреляции.

Отбор факторов для построения многофакторных моделей производится на основе качественного и количественного анализа социально-экономических явлений с использованием статистических и математических критериев.

1. По данным таблицы 1 лабораторной работы 6 построить корреляционную матрицу. В качестве результативного показателя выбрать ВРП.

Создаваемая в MS Excel с помощью инструментария «Анализ данных» корреляционная матрица имеет вид, приведенный в таблице 1.

Таблице 1

Общий вид корреляционной матрицы

	П₁	П₂	П₃	…	П_j	…	П_n
П₁	1
П₂	r₂₁	1
П₃	r₃₁	r₃₂	1
…	…	…	…	…
П_i	r_i1	r_i2	r_i3	…	1
…	…	…	…	…	…	…
П_n	r_n1	r_n2	r_n3	…	r_nj	…	1

Как видно из таблицы 1, корреляционная матрица представляет собой квадратную таблицу, по строкам и столбцам которой записаны наименования каждого показателя. В этой таблице: во-первых, r₁₁=1, r₂₂=1, r₃₃=1, … , r_ij=1, … , r_nn=1; во-вторых, r₁₂=r₂₁, r₁₃=r₃₁, … , r₁_n=r_n₁, и т.д.

Иными словами, в таблице 1 значения коэффициентов корреляции приведены дважды, в чем нет необходимости. Поэтому в MS Excel формируется лишь одна нижняя часть корреляционной матрицы. Коэффициент корреляции рассчитывается по формуле:

На рис. 1 представлен фрагмент окна построения корреляционной матрицы по данным регионов ЦФО России за 2016 г.

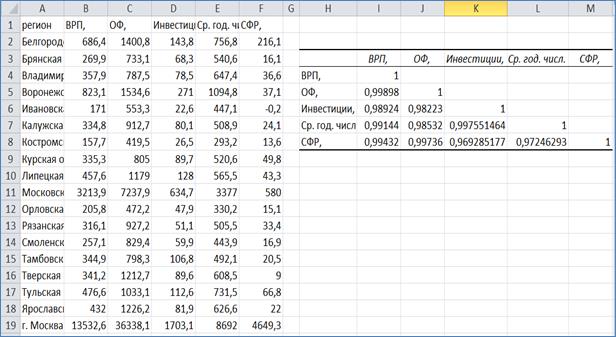
Рис. 1 Окно построения корреляционной матрицы по данным регионов ЦФО России за 2016 г. с помощью инструментария «Анализ данных» MS Excel

По корреляционной матрице можно:

- оценить степень тесноты связи (зависимости) каждого показателя от каждого из остальных (как известно, коэффициент линейной парной корреляции может принимать значения от -1 до 1, т.е. -1<r_ij<1. При этом, чем ближе значение r_ijк единице или минус единице, тем степень тесноты связи выше, при r_ij=0 – корреляция отсутствует, а при r_ij=±1 - связь является полной или функциональной);

- выявить направление связи, которое может быть положительным или отрицательным (если -1<r_ij<0, то изменение показателей с номерами i и j разнонаправлено, т.е. с ростом значений одного из них значения другого уменьшаются; если же 0<r_ij<1, то изменение показателей с номерами i и j однонаправлено, т.е. с ростом значений одного из них значения другого тоже растут).

2. Требуется изучить характер зависимости ВРП (или сальдированного финансового результата) от одного от среднегодовой стоимости основных фондов, инвестиций и среднегодовой численности занятых в экономике (заданных в таблице 1 лабораторной работы №6) при выборе каждого из следующих видов эконометрической модели: линейного, показательного, степенного, гиперболического, параболического видов. Методика построения соответствующих моделей аналогична парной регрессии (см лабораторную работу №5).

Лабораторная работа № 6 по дисциплине «Эконометрика»

Модуль 2. ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ ДИНАМИЧЕСКИХ ПРОЦЕССОВ

Тема 7. Методы и модели анализа динамики с помощью временных рядов

1. Прогнозирование на основе моделей временных рядов

По временным рядам основных экономических показателей предприятий Комитета по виноградарству, производству и обороту алкогольной и спиртосодержащей продукции РД за 2010-2016 гг., представленным в приложениях 1-3, каждому студенту для отдельного предприятия требуется:

- составить модели временных рядов линейного, показательного, степенного, гиперболического и параболического видов;

- оценить качество полученных моделей с помощью основных статистических характеристик;

- рассчитать прогнозные значения выбранного показателя на 2017-2019 гг. по различным моделям временных рядов. Для этого заполнить таблицу 1.

Таблица 1

Прогнозные значения показателя на 2017-2019 гг., полученные по различным моделям временных рядов по данным за 2010-2016 гг.

	лин	показ.	степ.	гип.	параб.
2017
2018
2019

На рисунке 1 представлен фрагмент компьютерной модели для построения уравнений временных рядов с помощью статистических функций MS Excel. В качестве Y выбрана выручка от реализации винограда (тыс. руб.) ГУП «Каякентский» за 2010-2015 гг.

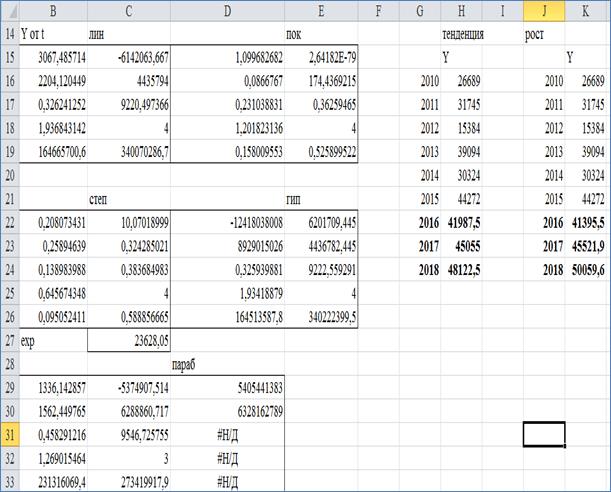
Рис 1. Фрагмент компьютерной модели для построения уравнений временных рядов выручки от реализации винограда ГУП «Каякентский» с помощью статистических функций MS Excel

Лабораторная работа № 7 по дисциплине «Эконометрика»

Модуль 2. ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ ДИНАМИЧЕСКИХ ПРОЦЕССОВ

Тема 7. Методы и модели анализа динамики с помощью временных рядов

2. Прогнозирование на основе моделей рядов динамики

- составить модели временных рядов затрат на основное производство (), основных средств () линейного вида;

- оценить качество полученных моделей с помощью основных статистических характеристик;

- составить модель рядов динамики линейной зависимости выручки от реализации продукции от факторов, указанных выше;

- оценить качество полученной модели с помощью основных статистических характеристик;

- рассчитать прогнозные значения выручки от реализации для отдельных хозяйств на 2017-2019 гг. по модели рядов динамики. Для этого заполнить таблицу 2.

Таблица 2

Прогнозные значения затрат на производство, основных средств и выручки от реализации продукции предприятий Комитета по виноградарству, производству и обороту алкогольной и спиртосодержащей продукции РД, рассчитанные по данным за 2010-2016 гг.

			y
2017
2018
2019

На рисунке 2 представлен фрагмент компьютерной модели для построения уравнений рядов динамики с помощью статистических функций MS Excel. В качестве Y выбрана выручка от реализации винограда (тыс. руб.) ГУП «Каякентский» за 2010-2015 гг.

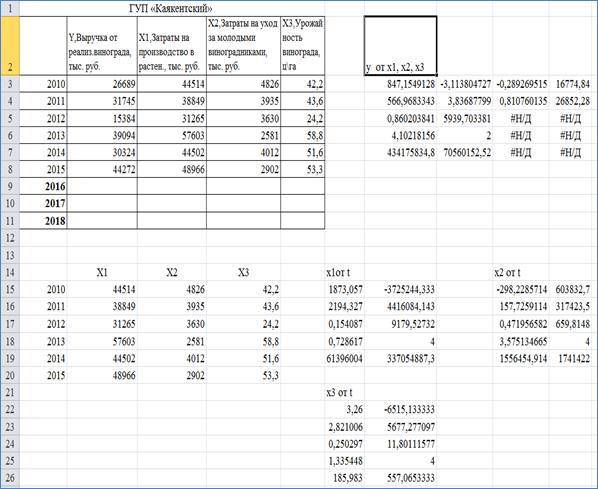
Рис 2. Фрагмент компьютерной модели для построения уравнений временных рядов и рядов динамики по данным ГУП «Каякентский» с помощью статистических функций MS Excel

Лабораторная работа № 8 по дисциплине «Эконометрика»

Модуль 2. ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ ДИНАМИЧЕСКИХ ПРОЦЕССОВ

Тема 8. Моделирование динамических процессов

Заданы ВРП и объем инвестиций Республики Дагестан за 2002-2015 гг. Представлены они в таблице 1.

Таблица 1

Исходные данные для построения уравнений с распределенным лагом

времени для зависимости ВРП региона от объема инвестиций

(по данным Республики Дагестан за 2002-2015 гг.)

Годы	ВРП, млрд. руб	Инвестиции, млрд. руб	Лаг=1	Лаг=2	Лаг=3
Годы	y_t	x_t	x_t-1	x_t-2	x_t-3
2002	31,6	5,5
2003	42,4	10,7	5,5
2004	54,9	13,5	10,7	5,5
2005	76,1	24,1	13,5	10,7	5,5
2006	96,9	39,4	24,1	13,5	10,7
2007	118,3	58,2	39,4	24,1	13,5
2008	166,7	86,3	58,2	39,4	24,1
2009	211,3	100,9	86,3	58,2	39,4
2010	265,1	115,1	100,9	86,3	58,2
2011	285,3	134,9	115,1	100,9	86,3
2012	327,0	152,4	134,9	115,1	100,9
2013	378,0	178,3	152,4	134,9	115,1
2014	429,5	211,6	178,3	152,4	134,9
2015	538,3	231,1	211,6	178,3	152,4

На рисунках 1и 2 представлены фрагменты компьютерной модели для построения и оценки уравнений с распределенным лагом времени.

Требуется:

- составить модели с распределенным лагом времени линейного вида для всех представленных на рисунках 1 и 2 комбинаций показателей-факторов. выписать отдельно к каждому уравнению соответствующие индексы детерминации;

- оценить качество полученных моделей с помощью основных статистических характеристик;

- рассчитать краткосрочный, промежуточные и долгосрочный мультипликаторы; определить средний и медианный лаги.

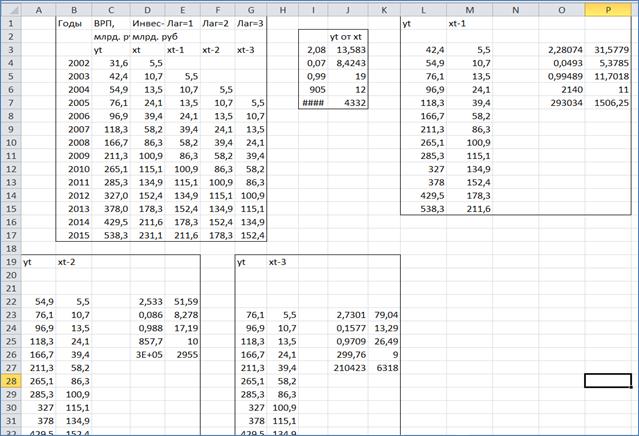
Рис 1. Фрагмент 1 компьютерной модели для построения и оценки уравнений с распределенным лагом времени с помощью простых статистических функций MS Excel

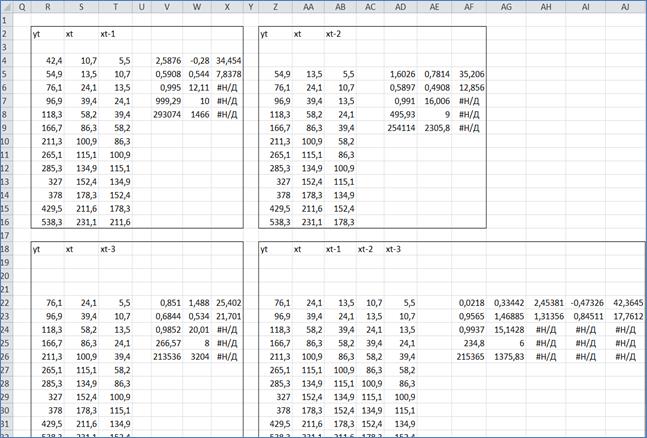
Рис 2. Фрагмент 2 компьютерной модели для построения и оценки уравнений с распределенным лагом времени с помощью простых статистических функций MS Excel

Приложения

Приложение 1

Затраты на основное производство предприятий Комитета по виноградарству, производству и обороту алкогольной и спиртосодержащей продукции РД, тыс. руб.

ГУП	2010	2011	2012	2013	2014	2015	2016
Комсомольское	4463	6466	9752	14668	12852	44949	35559
Башликент	5084	6192	9061	7383	9756	16579	16210
Утамышский	8208	10301	11931	18682	19021	26459	31216
Кр.Окт	9037	12843	14423	41207	31432	46109	79045
Усемикентский	9423	10274	15379	10242	10482	11201	22665
К.Маркса	13462	8729	6903	4797	935	2025	1218
Чкаловский	15297	14331	14107	12432	10656	11462	10601
Буйнакский	20878	18157	13005	17077	12042	11543	7869
Кировский»	25304	30139	27901	57965	51802	64449	63425
Каякентский	33767	39994	45926	67009	61126	61793	111474
Гергинский	42626	34300	27600	24178	15670	14496	12025
Каспий	46921	51664	54680	67888	65023	78601	82244

Приложение 2

Выручка от реализации продукции предприятий Комитета по виноградарству, производству и обороту алкогольной и спиртосодержащей продукции РД, тыс. руб.

ГУП	2010	2011	2012	2013	2014	2015	2016
Комсомольское	1654	2787	2461	16157	15760	25055	26841
Башликент	1854	2692	2453	11712	6542	13844	14542
Усемикентский	3990	4921	4921	9370	9674	12225	12293
Утамышский	5355	6998	6416	17590	14794	29387	18911
Кр.Окт	5955	8673	7879	38150	22776	40050	50399
Чкаловский	6044	6514	4932	11565	7066	13456	6648
К.Маркса	8983	6019	3681	4986	807	1400	938
Кировский»	11017	15425	11737	58830	53045	58781	63176
Буйнакский	12542	11801	7199	18431	8407	13020	6315
Гергинский	16039	15369	14714	21073	11335	9533	11877
Каякентский	18328	22562	22239	49258	36622	55721	59120
Каспий	25771	31877	27302	71668	67398	82020	73907

Приложение 3

Основные средства предприятий Комитета по виноградарству, производству и обороту алкогольной и спиртосодержащей продукции РД, тыс. руб.

ГУП	2010	2011	2012	2013	2014	2015	2016
Комсомольское	14051	18028	27877	27224	28071	55244	68053
Утамышский	8321	12513	18905	19607	70002	69890	77034
Чкаловский	22381	22416	22315	22533	22620	22778	22371
Буйнакский	41185	39887	41232	34688	35644	35049	34949
Усемикентский	45573	48134	49007	58321	56124	55274	66164
Кировский	48346	55172	63300	73121	78575	94642	107690
Башликент	52966	50915	49200	45702	45879	45118	40641
Каспий	57763	63210	71080	73905	81663	89877	101150
Кр.Окт	70492	78337	95073	91965	97972	117712	142421
Каякентский	173836	178819	196887	190387	176100	182948	231336

Список литературы

а) основная литература:

1. Эконометрика: учебник для академического бакалавриата / В. С. Тимофеев, А. В. Фаддеенков, В. Ю. Щеколдин. - 2-е изд., перераб. и доп. - М.: Издательство Юрайт, 2015. - 328 с.

2. Эконометрика : учебник и практикум для прикладного бакалавриата / В. И. Костюнин. - М.: Юрайт, 2014. - 285 с.

3. Эконометрика: учебник / В.С. Мхитарян, М.Ю. Архипова, В.А. Балаш, О. С. Балаш, Т.А. Дуброва, В.П. Сиротин. – М.: Проспект, 2015. – 384с.

4. Эконометрика: учебник для бакалавриата и магистратуры / под ред. Елисеевой И.И. – М.: Юрайт, 2016. – 449 с.

б) дополнительная литература:

1. Адамадзиев К. Р., Джаватов Д. К. Эконометрика. Краткий курс: учебное пособие. - Махачкала: Изд. Дом «Народы Дагестана», 2003. – 83с.

2. Айвазян С. А. Эконометрика-2. Продвинутый курс с приложениями в финансах / С. А. Айвазян. – М.: Инфра-М, 2015. – 944 с.

3. Валентинов В.А. Эконометрика. Практикум. – М. Дашков и К, 2016. – 436с.

4. Введение в эконометрику: учебник / М. Сток, М. Уотсон; пер. с англ. под науч. ред. М. Ю. Турунцевой. - М. : Дело : РАНХиГС, 2015. - 834 с.

5. Касимова Т.М. Экономико-математическое моделирование и прогнозирование развития регионального агропромышленного комплекса: монография / Т.М. Касимова. – Махачкала: Издательско-полиграфический центр ДГУ, 2017. – 149 с.

6. Компьютерные технологии анализа данных в эконометрике: Монография / Д.М. Дайитбегов. - 3-e изд., испр. и доп. - М.: Вузовский учебник: НИЦ Инфра-М, 2013. – 587с.