МИНОБРНАУКИ РОССИИ

ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Касимова Т.М.

МАТЕМАТИЧЕСКОЕ И ИМИТАЦИОННОЕ
МОДЕЛИРОВАНИЕ

Учебно-методическое пособие

для студентов очной формы обучения

по направлению 09.03.03 – «Прикладная информатика»

профили подготовки – «Прикладная информатика

в экономике», «Прикладная информатика в менеджменте», «Прикладная информатика в государственном

и муниципальном управлении»

Махачкала

Издательство ДГУ

2017

УДК 519.876.5

ББК 32.81-65с

К 281

Касимова Т.М.

Математическое и имитационное моделирование: учебно-методическое пособие. – Махачкала: Издательство ДГУ, 2017. – 80 с.

Учебно-методическое пособие предназначено для студентов очной формы обучения по направлению 09.03.03 – «Прикладная информатика» профили подготовки – «Прикладная информатика в экономике», «Прикладная информатика в менеджменте», «Прикладная информатика в государственном и муниципальном управлении», содержит теоретический и практический материал по основным разделам курса.

Рецензенты:

Алиев М.А. – профессор кафедры экономической теории ФГБОУ ВО «Дагестанский государственный педагогический университет», доктор экономических наук, профессор;

Ишталбагомаев Ш.М. – начальник отдела информационных технологий ПАО СК «Росгосстрах» в Республике Дагестан

Содержание

Введение

Лабораторная работа №1. Имитационный подход к моделированию

связей, зависимостей, динамических тенденций в экономике

Лабораторная работа №2. Модели процессов массового

обслуживания в экономических системах

Лабораторная работа №3. Реализация метода Монте-Карло в Excel

Лабораторная работа №4. Модели экономических задач

на выполнение прямых математических расчетов

Лабораторная работа №5. Имитационная модель для обоснования

прогноза развития предприятия

Лабораторная работа №6. Игровые методы обоснования

экономических и управленческих решений

Лабораторная работа №7. Имитационный подход

к моделированию межотраслевых балансов

Лабораторная работа №8. Производственные функции

Лабораторные работы № 9-11.Моделирование динамики

экономической системы (Производственные функции:

Модель Солоу)

Лабораторная работа №12. Экономико-математическая

модель международной торговли

Список использованной литературы

Введение

Имитационное моделирование, как известно, является эффективным инструментом исследования систем на различных этапах их жизненного цикла, включая проектирование, разработку и эксплуатацию.

Новые направления в применении имитационного моделирования связаны с их использованием для решения задач прогнозирования и принятия решений в процессе управления сложными системами.

Целью изучения дисциплины «Математическое и имитационное моделирование» является ознакомление студентов с новейшими достижениями в теории и практике имитационного моделирования, применяемыми в управлении, методами описания и анализа процессов управления, с особенностями различных типов задач принятия решений как в условиях определенности, так и в условиях неопределенности; с методами построения компьютерных моделей экономических и социальных систем, планирования машинных экспериментов и анализа полученных результатов.

В результате изучения дисциплины студент должен знать сферы эффективного применения имитационных моделей; основные этапы моделирования и задачи, решаемые на каждом из этих этапов; методы планирования, реализации и анализа результатов модельных экспериментов; возможности современных средств разработки имитационных моделей.

Изучив данную дисциплину, студент должен уметь грамотно формулировать задачи моделирования, выбирать наиболее эффективные виды моделей для решения этих задач, а также должен уметь осуществлять поставку и решение задачи имитационного моделирования конкретной экономической или социальной системы.

В процессе изучения данной дисциплины используются знания и навыки, полученные в рамках изучения дисциплин «Информатика и программирование», «Информационные системы», «Информационные технологии», «Компьютерное моделирование», «Проектирование информационных систем». Особый интерес и сложность при разработке данного учебного курса представляют лабораторные работы. Лабораторные работы выполняются студентами с использованием различных компьютерных программ.

Лабораторная работа №1. Имитационный подход к моделированию связей, зависимостей, динамических тенденций в экономике

1.1. Связи и зависимости в экономике, их математическое описание

Анализ и прогнозирование закономерностей, связей, зависимостей, динамических тенденций – сфера рыночной экономики, в которой широко применяется инструментарий математического моделирования, в первую очередь эконометрическое моделирование.

Особенность эконометрической модели состоит в том, что она описывает связи и зависимости для статистической совокупности (а не для отдельного наблюдения) и представляет собой одно уравнение.

Схематически эконометрическая модель записывается в виде уравнения

Y=f(X₁, X₂, …, X_n),

где Y – результативный показатель;

Х₁, Х₂, …, Х_n – показатели-факторы.

Вид эконометрической модели для выражения экономических связей и зависимостей в каждом конкретном случае заранее не известен. Он определяется в ходе постановки и решения задачи и зависит от объекта исследования, набора статистических наблюдений, количества показателей–факторов, включаемых в модели, от целей исследования и субъективного подхода автора и т.д.

Схематически любую эконометрическую модель можно свести к общему виду

Y = a₀ + a₁V₁ + a₂V₂ +…+ a_nV_n , (1)

где Y – результативный признак,

а₀, а₁, …, а_n – параметры,

V₁, V₂,…,V_n – простые переменные (показатели–факторы) или функции этих простых переменных.

Хотя вид эконометрической модели для конкретной задачи заранее не задается, должны быть известны математические аналоги (прототипы), на основе которых можно его определить и построить.

Примерами математических моделей, которые могут выступать в качестве аналогов (прототипов) эконометрических моделей, являются:

и т.д.

1.2. Методика построения эконометрических моделей. Выполнение расчетов на ПЭВМ

Построить эконометрическую модель означает, в первую очередь, рассчитать ее параметры (a₁, a₂, .., a_n).

Наиболее распространенным является метод наименьших квадратов. Согласно этому методу требуется найти такие значения a₁, a₂, .., a_n, при которых ∑(Y-Y_х)² принимала бы минимальное значение (где Y – фактические значения результативного показателя, Y_х – расчетные значения результативного показателя, получаемые на основе построенного эконометрического уравнения).

Для эконометрической модели (1) метод наименьших квадратов позволяет получит следующую систему уравнений для расчета параметров:

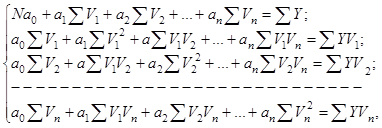
где N – число наблюдений статистической совокупности.

К наиболее важным характеристикам эконометрических моделей относятся: предельная эффективность показателя-фактора, коэффициент эластичности, изокванта, предельная норма заменяемости одного фактора другим, изоклиналь, коэффициенты и индексы корреляции и детерминации, стандартная ошибка и др.

Анализ параметров и характеристик необходим для выявления степени тесноты корреляционной зависимости (индекс корреляции и детерминация), для экономической интерпретации численных значений параметров, для расчета предельных норм заменяемости одних факторов другими, определения доверительных интервалов и др.

Численные значения параметров (их называют также коэффициентами регрессии) дают возможность ответить на вопрос: «На сколько изменится результативный показатель, т.е. Y, если тот или иной показатель-фактор х_iувеличится на единицу».

Интересным является анализ предельной нормы замены одного фактора другим, показывающей сколько единиц одного фактора требуется, чтобы заменить одну единицу другого фактора.

Важной частью анализа является определение доверительных интервалов с использованием стандартной ошибки.

Согласно теории вероятности и математической статистики, прогнозируемое значение результативного показателя будет находится в интервале

Y_расч- 2σ_у_lx ≤ Y_прогн≤ Y_расч. + 2σ_у_lx,

с вероятностью 95 %, где Y_расч. – значение результативного показателя, полученного по построенному уравнению при фактических значениях показателей-факторов; σ_ylx– стандартная ошибка.

Эконометрические модели применяются для прогнозирования. Для этого вне модели различными методами определяются численные значения показателей–факторов на прогнозируемый период; эти значения подставляются в построенное уравнение корреляционной зависимости и рассчитывается прогнозируемое значение результативного показателя; определяются доверительные интервалы.

1.3. Имитационное моделирование связей, зависимостей и динамических тенденций

Эконометрические модели могут быть рассмотрены как имитационные, если в условие задачи включить требования об изучении влияния на параметры и характеристики эконометрических моделей изменения:

а) выборки совокупности статистических наблюдений;

б) вида эконометрической модели;

в) отбора (включения, исключения) показателей-факторов в модели;

г) исключения из выборки отдельных наблюдений.

Выборка совокупности статистических наблюдений. В случае традиционной постановки задачи изучение связей и зависимостей может быть осуществлено на основе данных всей совокупности или ее частей (например, по федеральным округам; по выборке из ¼, 1/3, ½ регионов; по 3-4 региона из каждого округа и т.д.). В случае имитационного подхода в задачу включаются условия о том, как будут меняться связи и зависимости, если количество наблюдений в выборочной совокупности статистических данных будет меняться. Например, какие будут показатели связи для 87 регионов, 86, 85 и т.д.

Выбор вида эконометрической модели. В традиционном варианте постановки задачи целью является подбор одного наиболее приемлемого вида эконометрической модели на основе качественно-количественного анализа. В случае имитационного подхода задача сводится к изучению характера связей и зависимостей при выборе различных видов эконометрических моделей.

Отбор показателей-факторов модели. В традиционной постановке задача отбора факторов сводится к построению одного эконометрического уравнения, в которое включены один или несколько показателей-факторов, при условии, что дальнейшее их добавление не улучшает степень связи. В случае имитационного подхода задача сводится к определению влияния каждого из показателей-факторов и их комбинаций на параметры и характеристики эконометрических моделей.

Исключение из выборки отдельных наблюдений. В традиционном подходе к построению эконометрических моделей из выборки исключаются, как правило, наблюдения с аномальными значениями показателей, включаемых в модель. При имитационном подходе исключение из статистической совокупности отдельных наблюдений преследует цель выявить влияние каждого из наблюдений на степень и характер связей, зависимостей или динамических тенденций.

Задание 1. Заданы ВРП и стоимость основных фондов (млрд. руб.) регионов (см. таблицу 1). Требуется определить:

а) влияние каждого из регионов на тесноту связи между показателями и параметры, выражающие зависимость ВРП от среднегодовой стоимости ОФ в случае ее линейности;

б) имитировать особенности искомой зависимости за разные годы (2005, 2010, 2012, 2015).

Таблица 1

Валовой региональный продукт и стоимость основных фондов регионов ЮФО и СКФО за разные годы, млрд. руб.

регионы	2005		2010		2012		2015
регионы	ВРП	ОФ	ВРП	ОФ	ВРП	ОФ	ВРП	ОФ
Республика Адыгея	13,3	52	41,4	101	55,2	118	77,9	162
Республика Калмыкия	11,3	41	23,9	114	28,8	113	46	151
Краснодарский край	325,8	897	857,5	1870	1229,7	2471	1792,1	4209
Астраханская область	62,6	230	132,2	530	170,5	748	289	913
Волгоградская область	161,7	472	377,4	1116	499	1348	715,1	1735
Ростовская область	224,0	649	556,2	1331	761,8	1751	1000,2	2085
Республика Дагестан	76,1	257	265,1	610	327,0	823	538,3	1213
Республика Ингушетия	6,0	17	18,7	41	26,1	41	52,2	73
Кабар.-Балк. Республика	32,1	80	66,4	136	90,6	185	118,1	224
Карач.-Черк. Республика	14,5	60	38,6	112	49,6	126	69,2	166
Респ.СевОсетия - Алания	25,3	92	65,1	152	85,2	182	126,8	205
Чеченская Республика			64,1	208	86,3	301	141,3	414
Ставропольский край	132,8	395	277,5	799	399,9	980	541,2	1307

1. Рассчитать коэффициент корреляции по формуле:

;

2. Рассчитать стандартную ошибку по формуле:

;

3. Рассчитать параметры уравнения регрессии линейного вида по формулам:

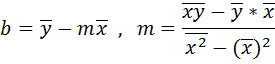
Для этого составить таблицу 2.

Таблица 2

Расчетная таблица для вычисления коэффициента корреляции, стандартной ошибки и параметров линейной регрессии

№ n/n	Регион	y	x
1
2
…
n
	Cумма			0	0
	Сред. арифметич.			-	-	-	-	-

Например, таблица для расчета показателей и параметров, выражающих зависимость ВРП от среднегодовой стоимости ОФ по данным регионов ЮФО и СКФО за 2015 год представлена в таблице 3.

Таблица 3

Расчетная таблица для вычисления коэффициента корреляции, стандартной ошибки и параметров линейной регрессии по данным регионов ЮФО и СКФО за 2015 год

№ региона n/n	y	x
1	77,9	162	-827	-345,7	683929,0	119540,4	285932,1
2	46,0	151	-838	-377,6	702244,0	142616,6	316467,5
3	1792,1	4209	3220	1368,5	10368400,0	1872665,9	4406421,4
4	289,0	913	-76	-134,6	5776,0	18129,6	10233,1
5	715,1	1735	746	291,5	556516,0	84945,3	217424,6
6	1000,2	2085	1096	576,6	1201216,0	332414,3	631903,0
7	538,3	1213	224	114,7	50176,0	13145,5	25682,5
8	52,2	73	-916	-371,4	839056,0	137972,2	340244,7
9	118,1	224	-765	-305,5	585225,0	93358,5	233742,8
10	69,2	166	-823	-354,4	677329,0	125632,1	291709,2
11	126,8	205	-784	-296,8	614656,0	88117,6	232727,4
12	141,3	414	-575	-282,3	330625,0	79719,4	162349,0
13	541,2	1307	318	117,6	101124,0	13818,9	37382,1
сумма	5507,4	12857	0	0	16716272,0	3122076,4	7192219,3
среднее	423,6	989	-	-	-	-	-

Результаты вычисления характеристик и параметров линейного уравнения регрессии привести в таблице 4. При этом для определения влияния каждого региона на тесноту связи между показателями и параметры, выражающие зависимость ВРП от стоимости ОФ исключить поочередно из исходной выборки каждый из регионов.

Таблица 4

Параметры и некоторые характеристики линейной зависимости ВРП от среднегодовой стоимости ОФ для различных выборок

Количество регионов
n
n-1(исключен 1-й регион)
n-1(исключен 2-й регион)
…
n-1(исключен n-й регион)

Сделать выводы о влиянии каждого из регионов на тесноту связи между показателями и параметрами, выражающими зависимость ВРП от среднегодовой стоимости ОФ.

Результаты выполнения пункта б) лабораторной работы №1 привести в виде таблицы 5.

Таблица 5

Параметры и некоторые характеристики линейной зависимости ВРП от стоимости ОФ за разные годы

Год
2005
2010
2011
2012

Сделать выводы о влиянии каждого периода наблюдений на степень и характер связей, зависимостей или динамических тенденций.

Задание 2.

Заданы некоторые социально-экономические характеристики Центрального ФО РФ в разрезе регионов за 2015 год.

Таблица 6

Некоторые социально-экономические показатели ЦФО РФ за 2015 год

регион	ВРП, млрд. руб.	ОФ, млрд. руб.	Инвестиции, млн. руб.	Ср. год. числ. занятых в эк., тыс. чел.
Белгородская обл.	619,4	699,1	146,4	699,1
Брянская область	243	533,6	61,7	533,6
Владимирская обл.	327,9	695,7	80,5	695,7
Воронежская область	709,1	1055,3	263,6	1055,3
Ивановская область	151,1	487,5	25,7	487,5
Калужская область	324,9	490,8	92,5	490,8
Костромская область	146,3	299,8	26,2	299,8
Курская область	297,4	567,1	70,4	567,1
Липецкая область	395,7	542,3	116,6	542,3
Московская область	2705,6	3040,5	640,3	3040,5
Орловская область	179,8	386,8	52,3	386,8
Рязанская область	297,3	494,1	54,1	494,1
Смоленская область	234,7	482,4	59,9	482,4
Тамбовская область	275,8	502,2	122,5	502,2
Тверская область	307,4	575,5	74,2	575,5
Тульская область	408,5	749,9	105,6	749,9
Ярославская область	388,1	627,4	69,1	627,4
г. Москва	12808,6	6778,4	1611,5	6778,4

Требуется изучить характер зависимости ВРП от одного из заданных в таблице 6 показателей (например, инвестиций) при выборе каждого из следующих видов эконометрической модели: линейного, показательного, степенного, гиперболического, параболического видов. Для этого необходимо составить таблицу 7.

Таблица 7

Расчетная таблица для построения моделей различных видов зависимости ВРП () от объема инвестиций () по данным регионов ЦФО за 2015 г.

№ региона n/n
1	619,4	146,4	6,43	4,99	0,007	146,4	21433,0
2	243	61,7	5,49	4,12	0,016	61,7	3806,9
3	327,9	80,5	5,79	4,39	0,012	80,5	6480,3
4	709,1	263,6	6,56	5,57	0,004	263,6	69485,0
5	151,1	25,7	5,02	3,25	0,039	25,7	660,5
6	324,9	92,5	5,78	4,53	0,011	92,5	8556,3
7	146,3	26,2	4,99	3,27	0,038	26,2	686,4
8	297,4	70,4	5,70	4,25	0,014	70,4	4956,2
9	395,7	116,6	5,98	4,76	0,009	116,6	13595,6
10	2705,6	640,3	7,90	6,46	0,002	640,3	409984,1
11	179,8	52,3	5,19	3,96	0,019	52,3	2735,3
12	297,3	54,1	5,69	3,99	0,018	54,1	2926,8
13	234,7	59,9	5,46	4,09	0,017	59,9	3588,0
14	275,8	122,5	5,62	4,81	0,008	122,5	15006,3
15	307,4	74,2	5,73	4,31	0,013	74,2	5505,6
16	408,5	105,6	6,01	4,66	0,009	105,6	11151,4
17	388,1	69,1	5,96	4,24	0,014	69,1	4774,8
18	12808,6	1611,5	9,46	7,38	0,001	1611,5	2596932,3

Параметры линейной модели оцениваются с помощью встроенной функции ЛИНЕЙН MS EXCEL, а показательного вида – ЛГРФПРИБЛ. Остальные модели сводятся к линейному виду посредством логарифмизации или введения замены.

Методические указания к построению эконометрических уравнений на примере линейной регрессии

Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии:

y=mx+b или y=m1x1 + m2x2 +...+ b,

где зависимое значение y является функцией независимого значения x. Значения m - это коэффициенты, соответствующие каждой независимой переменной x, а b - константа.

Синтаксис:

ЛИНЕЙН (известные значения y; известные значения x; конст; статистика)

известные значения y - это множество значений y, которые уже известны для соотношения y=mx+b.

Массив известные значения х может содержать одно или несколько множеств переменных.

Конст - это логическое значение, которое указывает, требуются ли, чтобы константа b была равна нулю. Константа принимает одно из двух значений ИСТИНА или ЛОЖЬ. Если конст имеет значение истина или опущено, то b вычисляется, если конст имеет значение ЛОЖЬ, то b полагается равным 0.

Статистика - это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.

Статистика также принимает одно из значений ИСТИНА или ЛОЖЬ. В первом случае дополнительная статистика рассчитывается, во втором случае не рассчитывается.

Дополнительные статистические характеристики функции ЛИНЕЙН приведены ниже Дополнительные статистические характеристики функции ЛИНЕЙН приведены ниже:

b, m₁, m₂,…m_n – коэффициенты регрессии (параметры модели);

se₁, se₂,...,se_n - стандартные значения ошибок для коэффициентов m₁,m₂,...,m_n;

se_b - стандартное значение ошибки для постоянной b;

r² - коэффициент детерминированности;

se_y - стандартная ошибка для оценки y;

F - F-статистика, используемая для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет;

df - степени свободы, используемые для нахождения F-критических значений в статистической таблице (для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой функции ЛИНЕЙН);

ss_reg - регрессионая сумма квадратов;

ss_resid - остаточная сумма квадратов.

Характеристики выводятся на экран дисплея в виде приведенного ниже массива (таблицы):

m_n	m_n-1	…	m₂	m₁	b
se_n	Se_n-1	…	se₂	se₁	se_b
r²	Se_у	…
F	Df	…
ss_reg	ss_resid	…

Порядок выполнения расчетов следующий:

1. Вводятся исходные данные или открывается существующий файл, содержащий исходные данные.

2. В рабочем окне Excel выделяется диапазон ячеек 5×(n+1) (5 число строк, (n+1) - число столбцов, n – число показателей факторов) для вывода результатов расчета.

3. Активизируется «Мастер функций» любым из способов:

а) в главном меню выбирается Вставка/Функция;

б) на панели инструментов Стандартная нажимается кнопка (f_x)

4. В появившемся окне "Мастер функций шаг 1 из 2" среди категорий выбирается Статистические, среди функций - ЛИНЕЙН шаг 1 из 2 (рис. 2)

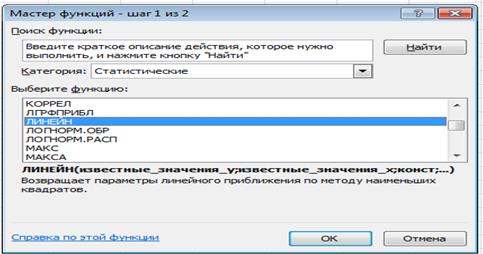
Рис. 2. Диалоговое окно «Мастер функций»

5. В появившемся втором окне "Мастер функций" (рис. 3) вводятся аргументы, т.е. указываются диапазоны ячеек рабочего окна EXCEL, в которых находятся исходные данные для У и Х, а также значения аргументов константа и статистика.

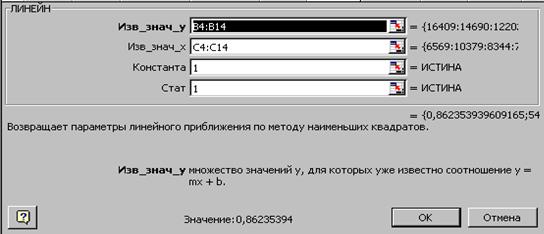
Рис. 3. Второе диалоговое окно «Мастер функций»

6. Нажимается кнопка ОК. В выделенном диапазоне рабочего окна Excel появляется результат - численное значение для коэффициента регрессии (b). Чтобы вывести всю статистику следует нажать клавишу <F2>, а затем - комбинацию клавиш <Ctrl>+<Shift>+<Enter>.

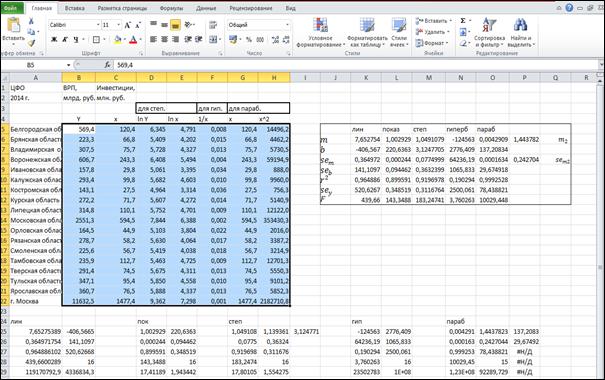
Рис. 4. Результаты построения эконометрических моделей различных видов

Результаты выполнения задания 2 привести в виде следующей таблицы 8.

Таблица 8

Параметры и статистические характеристики эконометрических моделей различных видов

лин	показ	степ	гиперб	параб

В таблице 8 – стандартное значение ошибки для параметра ,
- стандартное значение ошибки для постоянной ,
- коэффициент детерминированности, – стандартная ошибка для оценки , – F-критерий Фишера, – средняя ошибка аппроксимации.

По результатам сделать выводы о характере зависимости ВРП от инвестиций при выборе каждого из построенных видов эконометрических моделей.

Задание 3. Определить влияние каждого из показателей-факторов и их комбинаций на параметры и характеристики линейной эконометрической модели. В качестве результативного показателя выбрать ВРП, показателей-факторов – ОФ, инвестиции и среднегодовую численность занятых в экономике, заданные в таблице 6. Для этого необходимо составить таблицу 9.

Таблица 9

Параметры и статистические характеристики различных эконометрических моделей

от	от	от	от и	от и	от и	от ,,

Лабораторная работа №2. Модели процессов массового обслуживания в экономических системах

Задание 1 (одноканальная система с отказами).

Известно, что заявки на телефонные переговоры в телевизионном ателье поступают с интенсивностью λ заявок в час, а средняя продолжительность разговора по телефону мин. Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера.

Задание 2 (многоканальная система с отказами).

Определить оптимальное число телефонных номеров в телевизионном ателье для условий задания 1, если оптимальным считать удовлетворение в среднем из каждых 100 заявок не менее N заявок на переговоры.

Необходимые для расчетов величины λ, , N взять по варианту, заданному преподавателем, в таблице1.

Таблица 1

№ варианта
К задаче 1		1	2	3	4	5
λ заявок/час	90	90	85	70	75	80
, мин	2	1,5	2,5	2,0	2,5	1,5
К задаче 1		6	7	8	9	10
λ заявок/час	90	65	60	75	80	90
, мин	2	2,0	2,5	2,5	2,0	1,5
К задаче 2
N	90	85	90	90	90	85
N		80	80	80	70	90

Составьте и заполните следующие таблицы

Таблица 2

Расчет характеристик одноканальной СМО с отказами при различных интенсивностях потока заявок и обслуживания

	λ=	λ=	λ=
	μ=	μ=	μ=


A

Таблица 3

Расчет характеристик многоканальной СМО с отказами при различных интенсивностях потока заявок и обслуживания

	λ=	λ=	λ=
	μ=	μ=	μ=
	n=	n=	n=
ρ


A
Q

Порядок выполнения работы:

В качестве показателей эффективности СМО с отказами будем рассматривать:

А - абсолютную пропускную способность СМО, т.е. среднее число заявок, обслуживаемых в единицу времени;

Q - относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

Р_отк_. - вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;

- среднее число занятых каналов (для многоканальной системы).

Рассмотрим задачу одноканальной системы обслуживания с отказами.

При этом предполагается, что все потоки событий, переводимые СМО из одного состояния в другое, будут простейшими. Пусть имеется один канал, на который поступает поток заявок с интенсивностью. Поток обслуживаний имеет интенсивность . Требуется найти предельные вероятности состояний системы и показатели ее эффективности.

Система S имеет два состояния: S₀ - канал свободен, S₁ - канал занят. Размеченный граф состояний представлен на рис. 1.

Рис. 1.

В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид.

(1),

т.е. система вырождается в одно уравнение. Учитывая условие р₀ + p₁=1, найдем из (1) предельные вероятности состояний

(2)

которые выражают среднее относительное время пребывания системы в состоянии S₀ (когда канал свободен) и S₁ (когда канал занят), т.е. определяют соответственно относительную пропускную способность Q системы, вероятность отказа Р_отк_., и абсолютную пропускную способность А:

(3) (4) (5)

Пусть λ = 90 (1/ ч), мин.

Интенсивность потока обслуживаний λ =1/t0б =1/2 = 0,5(1/мин) = 30(1/час).

Относительная пропускная способность СМО:

Q = 30 / (90 + 30) = 0,25, т.е. в среднем только 25% поступивших заявок осуществят переговоры по телефону. Соответственно вероятность отказа в обслуживании составит: Ротк = 0,75.

Абсолютная пропускная способность СМО:

А = 90 * 0,25 = 22,5 , т.е. в среднем в час будут обслужены 22,5 заявки на переговоры. Очевидно, при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.

Граф состояний многоканальной СМО с отказами соответствует процессу гибели и размножения и показан на рис. 2.

Рис. 2.

Используя формулы процесса гибели и размножения, предельные вероятности состояния можно рассчитать по формулам

(6)

(7)

где - приведенная интенсивность потока заявок или интенсивность нагрузки канала.

Формулы (6) и (7) для предельных вероятностей получили названия формул Эрланга (Эрланг А.К. (конец XIX в. - начало XX в.) - датский инженер, математик - основатель теории массового обслуживания).

Вероятность отказа СМО, относительная и абсолютная пропускная способность, а также среднее число занятых каналов рассчитываются по формулам:

(8)

где p_k - предельные вероятности состояний (см. формулы (6) и (7)).

Среднее число занятых каналов можно найти и по формуле

(9)

Например, при n = 2

= = 0,118 = 0,12 ;

Q = 1 - (32 / 2 !) * 0,118 = 0,471 = 0,47 ;

A = 90 * 0,471 = 42,4 и т.п.

Для расчета вероятности того, что система свободна необходимо воспользоваться функцией СУММЕСЛИ EXCEL. При изменении числа каналов необходимо задавать новый критерий используемой встроенной функции.

Значения характеристик СМО сведем в таблицу 4.

Таблица 4

Характеристики обслуживания	Обозначение	Число каналов телефонных номеров
Характеристики обслуживания	Обозначение	1	2	3	4	5	6
Относительная пропускная способность	Q	0,25	0,47	0,65	0,79	0,90	0,95
Абсолютная пропускная способность	A	22,5	42,4	58,8	71,5	80,1	85,3

По условию оптимальности Q0,9, следовательно, в телевизионном ателье необходимо установить 5 телефонных номеров (в этом случае Q=0,90 - см. таблицу 1) . При этом в час будут обслуживаться в среднем 80 заявок (А = 80,1), а среднее число занятых телефонных номеров (каналов): К= 80,1/30=2,67 .

Задание 4 (одноканальная система с неограниченной очередью).

В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна l (судов в сутки). Среднее время разгрузки одного судна составляет tоб суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.

Задание 5 (одноканальная система с ограниченной очередью).

В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна l (судов в сутки). Среднее время разгрузки одного судна составляет суток. Предполагается, что очередь может быть ограниченной длины. Найти показатели эффективности работы причала, если в порту могут ожидать разгрузки не более чем 2 судна.

Необходимые для расчетов величины λ, взять по варианту, заданному преподавателем, в таблице 5.

Таблица 5

№ варианта	1	2	3	4
l судов/сутки	0,4	0,25	0,3	0,2
, сут	2	2	2	2
№ варианта	5	6	7	8
l судов/сутки	0,3	0,2	0,25	0,4
,сут	3	3	3	3

Составить таблицы для расчета показателей эффективности одноканальной СМО с неограниченной и ограниченной очередью аналогично таблицам 2 и 3 настоящей лабораторной работы.

Порядок выполнения работы:

В качестве показателей эффективности СМО с ожиданием (или очередью) кроме четырех вышеперечисленных применяются и следующие:

- среднее число заявок в системе (L_сист_.);

- среднее время пребывания заявки в системе (Т_cист.);

- среднее число заявок в очереди или длина очереди (L_оч_.);

- среднее время пребывания заявки в очереди (Т_оч);

- вероятность того, что канал занят или степень загрузки канала (Р_зан_.).

Пусть имеется одноканальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживаний - интенсивность μ. Требуется найти предельные вероятности состояний и показатели эффективности СМО.

Система может находиться в одном из состояний S₀, S₁, S₂, ..., S_k(рис. 3), по числу заявок, находящихся в СМО: S₀ - канал свободен; S₁ - канал занят (обслуживает заявку), очереди нет; S₂ - канал занят, одна заявка стоит в очереди; ... S_k - канал занят, (k-l) заявок стоят в очереди и т.д.

Рис. 3.

Предельные вероятности состояний можно определить по формулам:

(8)

Правая часть в этой формуле представляет собой геометрический ряд со знаменателем ρ < 1, равный . Поэтому p₀ = 1-ρ.

Предельные вероятности р₀, р₁, p₂, ..., р_k, ... образуют убывающую геометрическую прогрессию со знаменателем <1, следовательно, вероятность p₀ - наибольшая. Это означает, что если СМО справляется с потоком заявок (при <1), то наиболее вероятным будет отсутствие заявок в системе.

Среднее число заявок в системе L_сист_. можно определить по формуле математического ожидания:

L_сист_.= (9)

(суммирование от 1 до , так как нулевой член 0 р₀=0).

При <1формула (9) преобразуется к виду

L_сист_.=. (10)

Среднее число заявок в очереди (L_оч) очевидно равно

L_оч.=L_сист_.+L_об, (11)

где L_об. - среднее число заявок, находящихся под обслуживанием.

Среднее число заявок под обслуживанием представляет собой математическое ожидание числа заявок под обслуживанием, принимающего значения 0 (если канал свободен) либо 1 (если канал занят):

L_об.=0

Откуда

L_об.= 1-р₀ или L_об_. = ρ. (12)

На основе формул (10), (11) и (12) получим,

L_оч_.=. (13)

Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе и в очереди можно рассчитать по формулам заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.

T_сист_.= T_оч.=

Эти формулы называются формулами Литтла. Подставляя в формулу Литтла (6) значения L_сист. и L_оч. из (10) и (13) получим формулы для определения времени пребывания заявки в системе и среднего времени пребывания заявки в очереди -

T_сист_.= T_оч.=

Рассмотрим задачу многоканальной СМО с неограниченной очередью. Пусть имеется n-канальная СМО с неограниченной очередью. И пусть поток заявок, поступающих в СМО, имеет интенсивность , а поток обслуживаний - интенсивность . Требуется найти предельные вероятности состояний СМО и показатели ее эффективности.

Доказано, что при /n < 1 предельные вероятности существуют. Если /n1, очередь растет до бесконечности.

Показатели предельных вероятностей и эффективность в СМО с неограниченной очередью можно определить по формулам:

а) вероятность того, что заявка окажется в очереди,

P_оч.=,

б) среднее число занятых каналов

в) среднее число заявок в очереди

L_оч.=

г) среднее число заявок в системе

L_сист_.=L_оч.+. (14)

Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе находятся по формулам Литтла.

СМО с ограниченной очередью отличаются от рассмотренных выше задач лишь тем, что число заявок в очереди ограничено (не может превосходить некоторого заданного m). Если новая заявка поступает в момент, когда все места в очереди заняты, она покидает СМО необслуженной, т.е. получает отказ.

Для вычисления предельных вероятностей состояний и показателей эффективности таких СМО может быть использован тот же подход, что и выше, с той разницей, что суммировать надо не бесконечную прогрессию, а конечную.

Пусть l=0,4, .

Тогда получим следующие характеристики: Имеем r = l / m = l t об = 0,4 * 2 = 0,8 .

Так как r = 0,8 < 1 , то очередь на разгрузку не может бесконечно возрастать, и предельные вероятности существуют. Найдем их.

Вероятность того, что причал свободен: р0=1–0,8=0,2, а вероятность того, что он занят, Рзан = 1 - 0,2 = 0,8 .

Вероятности того, что у причала находится 1,2,3 судна (т.е. ожидают разгрузки 0,1,2 судна) равны:

р1 = 0,8 *(1 - 0,8) = 0,16;

р2 = 0,82 * (1 - 0,8) = 0,128;

р3 = 0,83 *(1 - 0,8) = 0,1024.

Вероятность того, что ожидают разгрузку не более чем 2 судна, равна

Р = р1 + р2 + р3 = 0,16 + 0,128 + 0,1024 = 0,3904.

Среднее число судов, ожидающих разгрузки,

= 0,82 / ( 1- 0,8 ) = 3,2, а среднее время ожидания разгрузки: = 3,2 / 0,8 = 4 (суток). Среднее число судов, находящихся у причала,

= 0,8 / (1 - 0,8) = 4 (суток) или = 3,2 + 0,8=4. Среднее время пребывания судна у причала:

= 4 / 0,8 = 5 (суток).

Очевидно, что эффективность разгрузки судов невысокая. Для еѐ повышения необходимо уменьшить среднее время разгрузки судна или увеличить число причалов n.

Лабораторная работа №3. Реализация метода Монте-Карло в Excel

Фирма рассматривает инвестиционный проект по производству продукта «А». В процессе предварительного анализа экспертами были выявлены три ключевых параметра проекта и определены возможные границы их изменений (табл. 1). Пусть все ключевые переменные имеют равномерное распределение вероятностей. Прочие параметры проекта считаются постоянными величинами в течение срока реализации проекта (табл. 2). В качестве результирующего показателя используется показатель чистого приведенного дохода (net present value, NPV).

Таблица 1

Ключевые параметры проекта по производству продукта «А»

Показатели	Сценарий
Показатели	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	150	300	200
Цена за штуку – P	40	55	50
Переменные затраты – V	35	25	30

Таблица 2

Неизменяемые параметры проекта по производству продукта «А»

Показатели	Наиболее вероятное значение
Постоянные затраты – F	500
Амортизация – A	100
Налог на прибыль – T	60%
Норма дисконта – r	10%
Срок проекта – n	5
Начальные инвестиции – I₀	2000

Проведение имитационных экспериментов по методу Монте-Карло в Excel можно осуществить двумя способами – с помощью встроенных функций и путем использования инструмента «Генератор случайных чисел» надстройки «Анализ данных».

1. Имитационное моделирование с применением встроенных функций Excel

Применение встроенных функций целесообразно лишь в том случае, когда вероятности реализации всех значений случайной величины считаются одинаковыми. Тогда для имитации значений требуемой переменной можно воспользоваться математическими функциями СЛЧИС() или СЛУЧМЕЖДУ(). Описание функций приведено в табл. 3.

Таблица 3

Математические функции Excel для генерации случайных чисел

Наименование функции		Формат функции	Описание
Английская версия	Русская версия	Формат функции	Описание
RAND	СЛЧИС	СЛЧИС() – не имеет аргументов	Возвращает равномерно распределенное случайное вещественное число, которое большее или равно 0 и меньше 1. Новое случайное вещественное число возвращается при каждом вычислении листа. Чтобы получить случайное вещественное число в диапазоне между a и b, можно использовать следующую формулу: СЛЧИС()(b-a*)+a
RANDBETWEEN	СЛУЧМЕЖДУ	СЛУЧМЕЖДУ (нижн_граница; верхн_граница)	Возвращает случайное целое число, находящееся в диапазоне между двумя заданными числами. При каждом вычислении листа возвращается новое случайное целое число.

Чтобы значения случайных чисел не изменялись при каждом пересчете листа, нужно отключить режим автоматических вычислений, выбрав на вкладке «Формулы» в раскрывающемся списке кнопки «Параметры вычислений» пункт «Вручную». Тогда пересчет листа будет осуществляться после нажатия клавиши F9.

Если с помощью этих формул различные значения для объемов выпуска, цен и затрат, то можно получить генеральную совокупность, содержащую различные значения исходных показателей и полученных результатов. После чего рассчитать соответствующие параметры распределения и провести вероятностный анализ.

На листе «Лр 3. Формулы» строим генеральную совокупность, задаем исходные значения и вводим формулы. Пример оформления листа приведен на рис. 1.

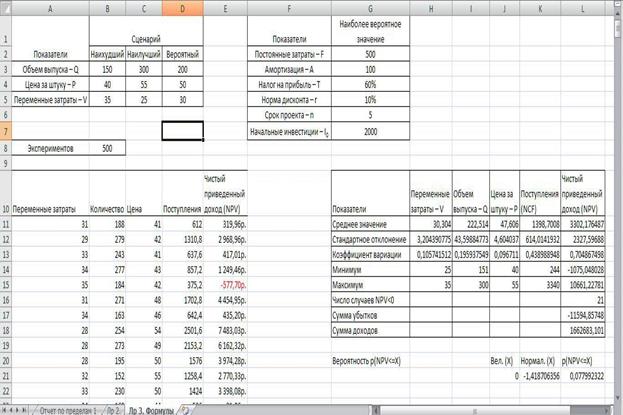
Рис. 1. Лист «Лр 3. Формулы»

Для ряда ячеек задаем имена, чтобы было их удобнее использовать при расчете: вкладка «Формулы», кнопка «Присвоить имя» (рис. 2).

Левая часть листа предназначена для ввода ключевых переменных, значения которых будут генерироваться в процессе проведения эксперимента. В ячейках $A$11:$A$510, $B$11:$B$510 и $C$11:$C$510 генерируют значения для соответствующих переменных с учетом заданных в ячейках В3:С5 диапазонов их изменений с помощью функции СЛУЧМЕЖДУ(нижн_граница; верхн_граница). Формулы в ячейках $D$11:$D$510 и $E$11:$E$510 вычисляют величину потока платежей и его чистую современную стоимость соответственно. Например, для ячейки D11 задается формула =(B11*(C11-A11)-Пост_затраты-Амортизация)*(1-Налог)+Амор-

тизация, а для ячейки E11 – формула =ПС(Дисконт;Срок;-D11)-Нач_инвест.

Функция ПС (ставка;кпер;плт;бс;тип) возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат. В функции ставка – процентная ставка за период, кпер – общее число периодов платежей по аннуитету, плт – выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ренты, бс – требуемое значение будущей стоимости или остатка средств после последней выплаты, тип – число 0 или 1, обозначающее срок выплаты. Параметры бс и тип являются необязательными.

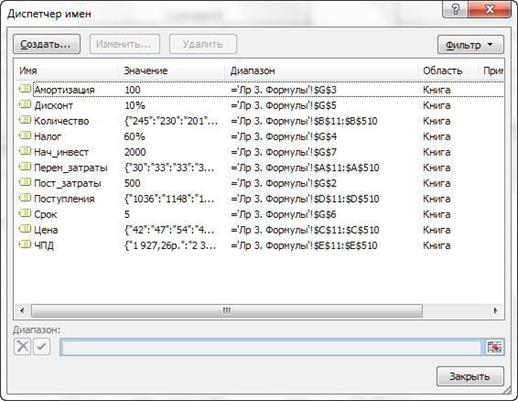
Рис. 2. Имена ячеек листа «Лр 3. Формулы»

В правой части листа кроме значений постоянных переменных содержатся также функции, вычисляющие параметры распределения изменяемых (Q, V, P) и результатных (NCF, NPV) переменных и вероятности различных событий. Соответствующие формулы приведены в табл. 4.

Здесь используются следующие формулы:

- СРЗНАЧ (число1, число2,...) возвращает среднее значение (среднее арифметическое) аргументов;

- СТАНДОТКЛОН (число1; число2; ...) оценивает стандартное отклонение по выборке., то есть меру того, насколько широко разбросаны точки данных относительно их среднего;

- МИН (число1;число2; ...) возвращает наименьшее значение в списке аргументов;

- МАКС (число1;число2; ...) возвращает наибольшее значение в списке аргументов;

- СЧЁТЕСЛИ (диапазон, критерий) подсчитывает количество ячеек в диапазоне, которые соответствуют одному указанному пользователем критерию;

- СУММЕСЛИ (диапазон, критерий, [диапазон_суммирования]) используется, если необходимо просуммировать значения диапазона, соответствующие указанным условиям. Если ячейки, по которым нужно выполнить суммирование, отличаются от ячеек, указанных в качестве диапазона, то их указывают в качестве необязательного диапазона суммирования.

Таблица 4

Формулы листа «Лр 3. Формулы»

Показатели	Переменные	Объем выпуска	Цена за штуку	Поступления	Чистый
	затраты (V)	(Q)	(P)	(NCF)	приведенный
					доход (NPV)

Среднее	=СРЗНАЧ(Пер	=СРЗНАЧ(Кол	=СРЗНАЧ(Це	=СРЗНАЧ(Пос	=СРЗНАЧ(ЧП
значение	ем_затраты)	ичество)	на)	тупления)	Д)
Стандартное	=СТАНДОТКЛ	=СТАНДОТКЛ	=СТАНДОТК	=СТАНДОТК	=СТАНДОТК
отклонение	ОН(Перем_зат	ОН(Количеств	ЛОН(Цена)	ЛОН(Поступл	ЛОН(ЧПД)
	раты)	о)		ения)
Коэффициент	=H12/H11	=I12/I11	=J12/J11	=K12/K11	=L12/L11
вариации
Минимум	=МИН(Перем_	=МИН(Количе	=МИН(Цена)	=МИН(Поступ	=МИН(ЧПД)
	затраты)	ство)		ления)
Максимум	=МАКС(Перем	=МАКС(Колич	=МАКС(Цена)	=МАКС(Посту	=МАКС(ЧПД)
	_затраты)	ество)		пления)
Число					=СЧЁТЕСЛИ(
случаев					ЧПД;"<0")
NPV<0
Сумма					=СУММЕСЛИ
убытков					(ЧПД;"<0")
Сумма					=СУММЕСЛИ
доходов					(ЧПД;">0")

В рассматриваемом примере сделано предположение о независимости и равномерном распределении ключевых переменных Q, V, P. Однако какое распределение при этом будет показатель NPV заранее определить нельзя. Одно из возможных решений этой проблемы – попытаться аппроксимировать неизвестное распределение каким-либо известным. При этом в качестве приближения удобнее всего использовать нормальное распределение. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет распределение, приблизительно соответствующее нормальному.

В прикладном анализе для целей аппроксимации широко применяется частный случай нормального распределения – так называемое стандартное нормальное распределение. Математическое ожидание стандартно распределенной случайной величины Е равно 0: M (E) = 0 . График этого распределения симметричен относительно оси ординат, и оно характеризуется всего одним параметром – стандартным отклонением s, равным 1.

Приведение случайной переменной E к стандартно распределенной величине Z осуществляется с помощью нормализации – вычитания средней и последующего деления на стандартное отклонение:

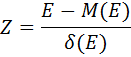
Следовательно, величина Z выражается в количестве стандартных отклонений. Для вычисления вероятностей по значению нормализованной величины Z используются специальные статистические таблицы.

В Excel подобные вычисления осуществляются с помощью статистических функций НОРМАЛИЗАЦИЯ() и НОРМСТРАСП():

- НОРМАЛИЗАЦИЯ(x;среднее;стандартное_откл) нормализует значение x для распределения, характеризуемого средним и стандартным отклонением;

- НОРМСТРАСП(z) возвращает стандартное нормальное интегральное распределение для значения z. Это распределение имеет среднее, равное нулю, и стандартное отклонение, равное единице. Данная функция используется вместо таблицы площадей стандартной нормальной кривой.

Эти функции заданы в ячейках K21 и L21. В ячейке L21 отображается вероятность того, что чистый приведенный доход будет меньше некоторого значения X. В примере, отображаемом на рис. Х, риск получить отрицательную величину чистого приведенного дохода не превышает 8%. Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка L17) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка L18) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.

2. Имитационное моделирование с применением инструмента «Генерация случайных чисел»

Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Использование этого инструмента возможно после установки надстройки «Анализ данных».

Рассмотрим ранее описанный пример. Также предположим, что распределение ключевых переменных является нормальным. Создайте копию листа «Лр 3. Формулы», переименуйте его в «Лр 3. Генерация», очистите диапазоны $A$11:$A$510, $B$11:$B$510 и $C$11:$C$510, а также внесите соответствующие изменения согласно рис. 3 и описанию ниже.

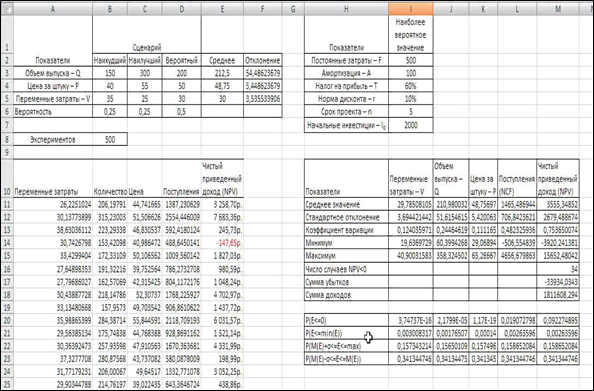
Рис. 3. Лист «Лр 3. Генерация»

Как следует из рис. 3 этот лист практически соответствует ранее разработанному для решения предыдущей задачи (см. рис. 1). Отличие составляют лишь формулы для расчета вероятностей, которые приведены в таблице 5 и небольшие дополнения к таблице со сценариями (вероятности, средние и отклонения), которые необходимы для расчета параметров распределений ключевых величин (табл. 6).

Таблица 5

Формулы для расчета вероятностей листа «Лр 3. Генерация»

Показате	Переменные	Объем	Цена за штуку	Поступления	Чистый
ли	затраты (V)	выпуска (Q)	(P)	(NCF)	приведенный
					доход (NPV)

P(E<=0)	=НОРМРАСП	=НОРМРАСП(	=НОРМРАСП(0	=НОРМРАСП(0	=НОРМРАСП(0;
	(0;I11;I12;1)	0;J11;J12;1)	;K11;K12;1)	;L11;L12;1)	M11;M12;1)
P(E<=min	=НОРМРАСП	=НОРМРАСП(	=НОРМРАСП(K	=НОРМРАСП(	=НОРМРАСП(M
(E))	(I14;I11;I12;1)	J14;J11;J12;1)	14;K11;K12;1)	L14;L11;L12;1)	14;M11;M12;1)
P(M(E)+s	=НОРМРАСП	=НОРМРАСП(	=НОРМРАСП(K	=НОРМРАСП(	=НОРМРАСП(M
<=E<=ma	(I15;I11;I12;1)-	J15;J11;J12;1)-	15;K11;K12;1)-	L15;L11;L12;1)-	15;M11;M12;1)-
x)	НОРМРАСП(I	НОРМРАСП(J	НОРМРАСП(K1	НОРМРАСП(L	НОРМРАСП(M1
	11+I12;I11;I12;	11+J12;J11;J12	1+K12;K11;K12;	11+L12;L11;L12	1+M12;M11;M12
	1)	;1)	1)	;1)	;1)
P(M(E)-	=НОРМРАСП	=НОРМРАСП(	=НОРМРАСП(K	=НОРМРАСП(	=НОРМРАСП(M
s<=E<=M	(I11;I11;I12;1)-	J11;J11;J12;1)-	11;K11;K12;1)-	L11;L11;L12;1)-	11;M11;M12;1)-
(E))	НОРМРАСП(I	НОРМРАСП(J	НОРМРАСП(K1	НОРМРАСП(L	НОРМРАСП(M1
	11-	11-	1-	11-	1-
	I12;I11;I12;1)	J12;J11;J12;1)	K12;K11;K12;1)	L12;L11;L12;1)	M12;M11;M12;1)

Обратите внимание на то, что для расчета стандартных отклонений используются формулы-массивы, то есть формулы, при помощи которых можно выполнять различные вычисления с одним или несколькими элементами в массиве (для ввода таких формул в рабочих книгах используется сочетание клавиш CTRL+SHIFT+ВВОД).

Таблица 6

Формулы для расчета параметров распределения листа «Лр 3. Генерация»

Показатели	Среднее	Отклонение
Объем выпуска – Q	=СУММПРОИЗВ(B3:D3;$B$6:$D$6)	{=КОРЕНЬ(СУММПРОИЗВ((B3:D3- E3)^2;$B$6:$D$6))}
Цена за штуку – P	=СУММПРОИЗВ(B4:D4;$B$6:$D$6)	{=КОРЕНЬ(СУММПРОИЗВ((B4:D4- E4)^2;$B$6:$D$6))}
Переменные затраты – V	=СУММПРОИЗВ(B5:D5;$B$6:$D$6)	{=КОРЕНЬ(СУММПРОИЗВ((B5:D5- E5)^2;$B$6:$D$6))}

Функция НОРМРАСП (x; среднее; стандартное_откл; интегральная) возвращает нормальную функцию распределения для значения x для указанного среднего и стандартного отклонения. Параметр «интегральная» - логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.

Задайте значения вероятностей: 0,5 для вероятного сценария и по 0,25 для каждого из наилучшего и наихудшего сценариев.

Проведение имитационного эксперимента заключается в следующем: на вкладке «Данные» в меню «Анализ данных» выберите пункт «Генерация случайных чисел». В появившемся диалоговом окне выберите тип распределения «Нормальное», заполните остальные поля согласно рис. 4 и нажмите кнопку ОК. В результате переменные затраты будут заполнены сгенерированными случайными значениями. Аналогично заполните количества и цены.

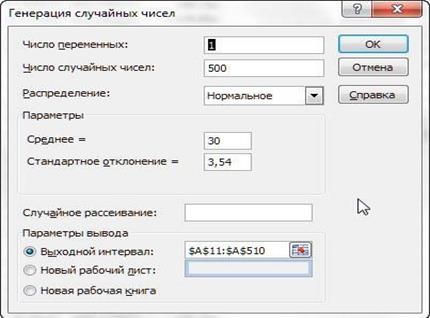
Рис. 4. Заполнение полей окна «Генератор случайных чисел»

При заполнении полей окна «Генератор случайных чисел» следует обратить внимание, что параметры «Среднее» и «Стандартное отклонение» можно задать только в виде констант. Использовать адреса ячеек и собственные имена не допустимо! Указание аргумента «Случайное рассеивание», равным 1, позволяет при повторных запусках генератора получать те же значения случайных величин, что и при первом.

Результаты (рис. 3) проведенного имитационного эксперимента ненамного отличаются от предыдущих (рис. 4). Величина ожидаемого чистого приведенного дохода (NPV) равна 3555,35 при стандартном отклонении 2679,49. Коэффициент вариации (0,75) немного выше, чем в предыдущем случае, но меньше 1, таким образом, риск данного проекта в целом ниже среднего риска инвестиционного портфеля фирмы. Результаты вероятностного анализа показывают, что шанс получить отрицательную величину NPV не превышает 9%. Общее число отрицательных значений NPV в выборке составляет 34 из 500. Таким образом, с вероятностью около 91% можно утверждать, что чистый приведенный доход проекта будет больше 0. При этом вероятность того, что величина NPV окажется больше чем М(NPV)+s, равна 16% (ячейка M22). Вероятность попадания значения NPV в интервал [М(NPV)-s; М(NPV)] равна 34%.

Лабораторная работа №4. Модели экономических задач на выполнение прямых математических расчетов

Модель экономической задачи на выполнение прямых математических расчетов представляет собой совокупность формул, с помощью которых на основе заданных исходных экономических показателей рассчитываются зависимые от них промежуточные и конечные экономические показатели, характеризующие различные стороны хозяйственной деятельности.

Методика построения моделей прямых математических расчетов сводится к следующему:

- формулировка решаемой задачи;

- осуществление численного решения (построение алгоритма решения) задачи;

- ввод символьных обозначений для исходных, промежуточных и конечных расчетных показателей;

- запись в принятых обозначениях алгоритма решения задачи (совокупность формул).

Методику построения моделей прямых математических расчетов рассмотрим на конкретном примере.

Пример 1. Формулировка решаемой задачи. На предприятии из трех видов сырья вырабатывается пять видов продукции (А, Б, В, Г, Д).

Объем вырабатываемой продукции в натуральном выражении (шт.), нормы расхода сырья (кг/шт.), цены сырья (руб./кг) и продукции (руб./шт.) приведены в таблице 1:

Таблица 1

Виды сырья	Виды продукции и нормы расхода сырья					Цена единицы сырья
Виды сырья	А	Б	В	Г	Д	Цена единицы сырья
1	0,5	0,4	0,3	0,4	0,6	900
2	0,3	0,6	0,8	0,5	0,3	1200
3	0,6	0,2	0,3	0,4	0,5	700
Объем продукции	1700	3400	2100	1800	2700
Цена единицы продукции	1400	1000	1900	1300	1500

Требуется: 1) определить потребность в сырье на производство всей продукции и материалоемкость продукции; 2) построить модель для выполнения прямых математических расчетов.

Численное решение (построение алгоритма) задачи.

Потребность в сырье равна:

первого вида – 1700∙0,5 + 3400∙0,4 + 2100∙0,3 + 1800∙0,4 + 2700∙0,6 = В1;

второго вида – 1700∙0,3 + 3400∙0,6 + +2100∙0,8 + 1800∙0,5 + 2700∙0,3 = В2;

третьего вида – 1700∙0,6 + 3400∙0,2 + +2100∙0,3 + 1800∙0,4 + 2700∙0,5= В3.

Для определения материалоемкости продукции рассчитываем суммарные затраты и объем продукции в денежном выражении:

- суммарные материальные затраты – В1∙900 + В2∙1200 + В3∙700 = МЗ;

- объем продукции в денежном выражении – 1700∙1400 + 3400∙1000 + 2100∙1900 + 1800∙1300 + 2700∙1500 = ОП;

- материалоемкость продукции – МЗ/ОП = Ме.

Построение модели:

1. Ввод обозначений для исходных показателей:

А₁, B₁, C₁, D₁, E₁ – нормы расхода первого вида сырья на производство продукции А, Б, В, Г, Д соответственно (кг);

А₂, B₂, C₂, D₂, E₂ – нормы расхода второго вида сырья на производство продукции А, Б, В, Г, Д соответственно (кг);

А₃, B₃, C₃, D₃, E₃ – нормы расхода третьего вида сырья на производство продукции А, Б, В, Г, Д соответственно (кг);

Z₁,Z₂, Z₃ – цены единицы первого, второго и третьего вида сырья (руб./кг);

Z_A,Z_B, Z_C, Z_D,Z_E – цены единицы продукции А, Б, В, Г, Д соответственно (руб./шт.);

V_A,V_B, V_C, V_D,V_E – объем продукции А, Б, В, Г, Д в натуральном выражении (шт.).

2. Ввод обозначений для расчетных показателей:

PS₁, PS₂, PS₃ – потребность в сырье первого, второго и третьего видов (кг);

MZ – суммарные материальные затраты (тыс. руб.);

V - объем продукции в денежном выражении (тыс. руб.);

ME – материалоемкость продукции (руб.).

3. Математическая запись модели:

PS₁ = V_A∙ А₁ + V_B∙B₁ + V_C∙C₁ + V_D∙D₁ + V_E∙E₁;

PS₂ = V_A∙ А₂ + V_B∙B₂ + V_C∙C₂ + V_D∙D₂ + V_E∙E₂;

PS₃ = V_A∙ А₃ + V_B∙B₃ + V_C∙C₃ + V_D∙D₃ + V_E∙E₃;

MZ = PS₁∙Z₁+ PS₂∙Z₂ + PS₃∙Z₃;

V = V_A∙Z_A+ V_B∙ Z_B + V_C∙Z_C+ V_D∙Z_D+ V_E∙Z_E;

Решение на ПЭВМ в Microsoft Excel:

1. Запуск MS Excel;

2. Ввод в рабочее окно данных таблицы 1;

3. Создание таблицы 2;

4. Ввод формул в столбец “Величина показателя” таблицы 2;

5. Сохранить результаты решения задачи 1;

6. Выбор наиболее приемлемого варианта решения задачи.

Таблица 2

Потребность в сырье и материалоемкость продукции

№№ п/п	Наименование показателя	Единицы измерения	Величина показателя
1	Потребность в сырье:
	а) первого вида	кг
	б) второго вида	кг
	в) третьего вида	кг
2	Стоимость сырья (материальных затрат)	тыс.руб.
3	Стоимость продукции	тыс.руб.
4	Материалоемкость продукции	руб.

Модели прямых экономических расчетов могут рассматриваться как имитационные, если ставиться задачи с их помощью изучить изменения расчетных (итоговых) показателей в зависимости от изменения исходных показателей, принимаемых в качестве управляющих параметров. К управляющим обычно относятся такие показатели, которые могут изменятся под влиянием объективных или субъективных факторов и которые оказывают существенное влияние на итоговые (расчетные) экономические показатели.

В примере 1 к управляющим можно отнести цены на сырье, объем производства отдельных видов продукции в натуральном выражении, цены на продукцию. При этом цены на сырье формируются на рынке и от предприятия практически не зависит. Объем производства отдельных видов продукции является показателем, целиком зависящим от предприятия. Цены на различные виды продукции в значительной степени также зависят от предприятия. Однако на цены оказывают влияние и предприятия-конкуренты. Следовательно, задача предприятия, меняя управляющие параметры (цены на сырье, объем продукции в натуральном выражении, цены на продукции) разработать вариант плана производства продукции.

В случае имитационной постановки в формулировку задачи вводятся следующие изменения:

- вместо фиксированных цен на сырье вводятся диапазоны цены (например, цена 1-го вида сырья колеблется в пределах 900-1100 руб., 2-го вида сырья – 1200-1400 руб., 3-го вида сырья – 700-800 руб.);

- вместо фиксированного объема продукции в натуральном выражении вводятся верхний и нижний предел ее производства (например, продукция вида А должно быть произведено не более 1800 и не менее 1700 и т.д.);

- вместо цены на продукцию также устанавливается возможный диапазон ее изменения (например, цена продукции А может колебаться в пределах 1400-1600 руб. и т.д.).

Заключительная часть задачи меняется полностью. Она формулируется следующим образом: Требуется: 1) построить имитационную модель для определения зависимости потребности в сырье на производство продукции и материалоемкости продукции от изменения цен на сырье и продукцию, а также от объема производства отдельных видов продукции; 2) путем выполнения расчетов на ПЭВМ выявить зависимость потребности в сырье на производство продукции, величины материальных затрат, объема продукции в денежном выражении и материалоемкости продукции от изменения управляющих параметров.

Таблица, иллюстрирующая имитационный подход, приведена в таблице 3.

Таблица 3

Имитация определения потребности в сырье и материалоемкости продукции

№№ п/п	Наименование показателя	Единицы измерения	При изменении цены единицы сырья
№№ п/п	Наименование показателя	Единицы измерения	1-го	2-го	3-го
1	Потребность в сырье:
	а) первого вида	кг
	б) второго вида	кг
	в) третьего вида	кг
2	Материальные затраты	тыс.руб.
3	Стоимость продукции	тыс.руб.
4	Материалоемкость продукции	руб.

Продолжение таблицы 3

	При изменении объема продукции					При изменении цены на единицу продукции
	А	Б	В	Г	Д	А	Б	В	Г	Д
1



2
3
4

Лабораторная работа №5. Имитационная модель для обоснования прогноза развития предприятия

Методы обоснования прогноза развития предприятия могут быть разными в зависимости от выбора исходных условий и конечных целей. Один из возможных способов такого обоснования проиллюстрируем на конкретном примере. Пусть для предприятия задана совокупность различных групп показателей, характеризующих уровень его развития за определенный период: затратно-ресурсных, результативных, нормативных и эффективности производства (таблица 1).

На основе этих показателей составляется ряд возможных вариантов развития предприятия. В таблице 2 предложено десять таких вариантов.

Таблица 1

Перечень показателей, характеризующих уровень развития предприятия

1. Затратно-ресурсные (тыс. руб.)	2. Результативные (тыс. руб.)	3. Нормативные (%)	4. Эффективности производства
1.1. Материальные затраты	2.1. Объем продукции	3.1. Норма амортизации	4.1. Производитель ность труда, тыс. руб.
1.2. Среднегодовая стоимость основных производственных фондов	2.2. Суммарная величина прибыли	3.2. Норматив начислений на зарплату	4.2. Фондоотдача, руб.
1.3. Численность работников	2.3. Платежи за кредит	3.3. Ставка платежа за кредит	4.3. Рентабельность продукции, %
1.4. Фонд оплаты труда	2.4. Налог на прибыль	3.4. Ставка налога на прибыль	4.4. Материало- емкость продукции, руб.
1.5. Среднемесячная зарплата	2.5. Прибыль для предприятия		4.5. Затраты на 1 руб. продукции, руб.
1.6. Начисления на зарплату
1.7. Амортизационные отчисления
1.8. Суммарные производственные затраты
1.9. Сумма кредитов

Варианты отличаются друг от друга перечнями задаваемых и рассчитываемых показателей (исходными условиями и конечными целями). В таблице 2 заданные показатели обозначены знаками плюс (+), расчетные – знаками минус (-). В шестом столбце таблицы объединены пять вариантов, от VI до X, образованных по схеме: четыре затратно-ресурсных показателя + два нормативных показателя + один показатель эффективности. При этом каждые шесть первых из исходных показателей в VI-X вариантах одни и те же. Отличаются они друг от друга лишь одним из заданных показателей эффективности, обозначенных в таблице знаком плюс с вопросительным знаком (+?).

Таблица 2

Возможные варианты прогноза развития предприятия, включенные в модель

Показатели и их обозначения		Варианты
Показатели и их обозначения		I	II	III	IV	V	VI
1.1.	M	+	-	-	+	-	+
1.2.	F	+	-	-	-	+	+
1.3.	CH	+	-	+	+	+	+
1.4.	Z	+	-	-	-	-	+
1.5.	ZP	-	+	+	+	+	-
1.6.	SS	-	-	-	-	-	-
1.7.	A	-	-	-	-	-	-
1.8.	S	-	-	-	-	-	-
1.9.	CR	+	+	+	+	+	+
2.1.	V	+	+	+	+	+	-
2.2.	P
2.3.	PCR	-	-	-	-	-	-
2.4.	NAL	-	-	-	-	-	-
2.5.	XP	-	-	-	-	-	-
3.1.	HA	+	+	+	+	+	+
3.2.	HS	+	+	+	+	+	+
3.3.	HCR	+	+	+	+	+	+
3.4.	HNAL	+	+	+	+	+	+
4.1.	PT	-	+	-	-	-	+?
4.2.	FO	-	+	+	-	-	+?
4.3.	R	-	-	-	-	-	+?
4.3.	ME	-	+	+	-	-	+?
4.5.	SV	-	-	-	+	+	+?

Имитационная модель для прогнозирования развития предприятия представляет собой совокупность формул по определению расчетных показателей на основе исходных. Каждый вариант развития предприятия имеет свой математический алгоритм расчетов, но все они представляют собой модификации одних и тех же расчетных формул (обозначения модели см. в таблице 2):

(1)	(2) Z = ZP ;
(3)	(4) S = M + Z + SS + A;
(5) P = V – S;	(6) ;
(7)	(8) ;
(9)	(10) ;
(11)	(12) ;
(13) XP = P – PCR – NAL.

Например, первая формула имеет две модификации:

Модификациями второй формулы являются:

Z = ZP ; и

Пятая формула имеет три модификации:

P =V – S; V = S + P и S = V – P и т.д.

В имитационную модель, кроме вышеуказанных формул, включены также:

а) формулы, позволяющие определить место каждого варианта в их совокупности по величине показателей эффективности в каждом варианте делятся на их численное значение в одном из вариантов, принимаемом за основу (например, в первом варианте).

Эти формулы имеют вид:

(14) - для показателей PT,FO,R, i = ; j = 1,2 3

(15) - для показателей ME, SV, i = ; j = 4, 5,

где Е_i - численное значение показателя эффективности в i-м варианте; E₁ – численное значение показателя эффективности в первом варианте;

б) формула для определения места каждого варианта по интегральному показателю эффективности:

(16) i = ,

где IE_i – интегральный показатель для i-го варианта;

в) формулы для расчета компромиссных вариантов, которые могут быть разработаны путем сочетания различных комбинаций предложенных вариантов (из трех, четырех или пяти наилучших вариантов и т.д.) или на основе всех десяти.

При этом затратно-ресурсные показатели и результативные показатели компромиссных вариантов рассчитываются как среднее арифметическое вариантов, служащих их основой, а показатели эффективности – так же, как и в других вариантах.

Решение на ПЭВМ в MS Excel:

1. Запуск MS Excel;

2. Создание в рабочем окне Excel таблицы 2 (таблица должна содержать 10 столбцов – по столбцу для каждого варианта);

3. Ввод в таблицу исходных показателей (см. таблицу 2, клетки со знаком «+»);

4. Ввод формул для определения расчетных показателей (см. таблицу 2, клетки со знаком «-») и выполнение расчетов;

Фрагмент выполнения задания представлен на рисунке 1.

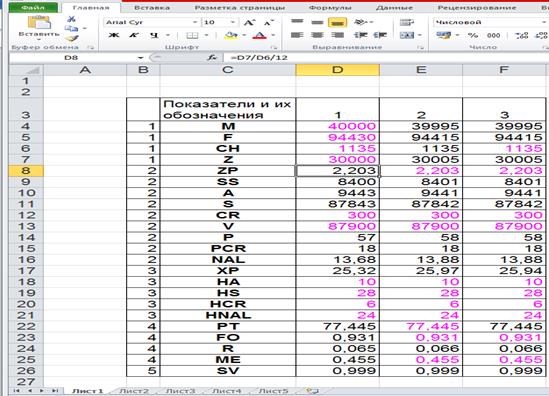
Рис.1. Окно расчета показателей, характеризующих уровень развития предприятия для некоторых вариантов

5. Создание таблицы 3;

Таблица 3

		варианты
		1	2	3	4	5	6	7	8	9	10
1	PE для PT
2	PE для FO
3	PE для R
4	PE для ME
5	PE для SV
6	IE

6. Ввод формул в таблицу 3 и выполнение расчетов;

7. Сохранение результатов;

8. Строка IE таблицы 3 характеризует эффективность варианта прогноза развития предприятия. Наилучшим является вариант с наибольшими значениями IE. По мере развития IE эффективность варианта снижается.

Отличительные особенности этой задачи:

- возможность выявления влияния одних и тех же управляющих параметров на расчетные показатели прогноза (имитация в пределах каждого варианта);

- возможность выявления влияния различных исходных управляющих параметров на расчетные показатели прогноза (имитация по выявлению наиболее эффективного варианта управляющих параметров среди всех рассматриваемых).

Лабораторная работа №6. Игровые методы обоснования экономических и управленческих решений

Случаи, когда между участниками игры отсутствует «антагонизм» (например, в процессе работы предприятий и торговых посредников) называют «играми с природой».

Решения могут приниматься по результатам анализа ряда критериев. К их числу относятся критерии: основанный на известных вероятностных состояниях «природы»; максиминный Вальда; пессимизма-оптимизма Гурвица; минимаксного риска Сэвиджа. Критерий, основанный на вероятностных состояниях.

Если известны вероятности состояний «природы» (например, спроса по данным анализа за прошлые годы):

где ,

то в качестве показателя эффективности (рациональности, обоснованности) стратегии берется средний (математическое ожидание) - выигрыш применения этой стратегии:

а оптимальной считают стратегию, для которой этот показатель эффективности имеет максимальное значение, то есть

Если каждому решению соответствует множество возможных результатов с вероятностями , то среднее значение выигрыша можно определить по формуле

а оптимальная стратегия выбирается по условию

Можно воспользоваться и стратегией минимального среднего риска для каждого i-го состояния «природы»

Максиминный критерий Вальда предполагает выбор решения, при котором гарантируется максимальный выигрыш в наихудших условиях внешней среды (состояния «природы»):

Согласно критерия пессимизма-оптимизма Гурвица при выборе решения вместо двух крайностей в оценке ситуации (оптимум-пессимизм) придерживаются некоторого компромисса, учитывающего возможность как наихудшего, так и наилучшего поведения «природы»:

где x - показатель пессимизма-оптимизма (чаще всего 0,5).

Если х = 1 критерий слишком пессимистичный, если х = 0 – слишком отптимистичный.

По критерию минимаксного риска Сэвиджа выбирают ту стратегию, при которой величина риска имеет минимальное значение в самой неблагоприятной ситуации:

Комплексный анализ всех этих критериев позволяет в определенной степени оценить возможные последствия принимаемых решений.

При анализе «игры с природой» вводится показатель влияния какого-либо состояния «природы» на исход продаж, то есть показатель риска равный

из которых составляется матрица рисков.

Задание 1. Известна матрица условных вероятностей P_ij продажи старых товаров С₁, С₂, С₃ при наличии новых товаров Н₁, Н₂, Н₃ (табл. 1).

Таблица 1

Платежная матрица

Старые

товары

Новые товары

Н₁

Н₂

Н₃

С₁

С₂

С₃

0,6

0,2

0,1

0,3

0,7

0,4

0,1

0,5

Требуется определить наиболее выигрышную политику продаж по каждому из следующих критериев: по известным вероятностным состояниям; Вальда; Гурвица; Сэвиджа.

Шаг 1. Необходимо составить таблицу 2.

Таблица 2

Расчетная таблица для промежуточных вычислений

1	2	3	4	5	6	7	8	9	10




				max		max	max		max

В таблице 1 элементы платежной матрицы и матрицы вероятностей известны, элементы матрицы рисков необходимо найти по соответствующей формуле.

Значение (показатель пессимизма-оптимизма) принять равным , если он не задан по условию задачи.

Шаг 2. Выделить максимальный элемент в соответствующей строке каждого из столбцов 5, 7, 8 и 10 таблицы 2.

Шаг 3. Результаты решения задачи привести в виде табл.3.

Таблица 3

Возможные варианты продаж, полученные по различным критериям

Критерий

По известным

вероятностным

состояниям

Вальда

Гурвица

Сэвиджа

Оптимальный план продаж

Выбрать изделие, соот-щее выделенному

эл-ту столбца 7

Выбрать изделие, соот-щее выделенному эл-ту столбца 5

Выбрать изделие, соот-щее выделенному эл-ту столбца 8

Выбрать изделие, соот-щее выделенному эл-ту столбца 12

Лабораторная работа №7. Имитационный подход при моделировании межотраслевых балансов

Идея сбалансированности лежит в основе всякого рационального функционирования хозяйства. Суть ее в том, что все затраты должны компенсироваться доходами хозяйства. В основе создания балансовых моделей лежит балансовый метод – взаимное сопоставление имеющихся ресурсов и потребностей в них.

Межотраслевой баланс отражает производство и распределение валового национального продукта по отраслям, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.

Пусть весь производственный сектор народного хозяйства разбит на чистых отраслей. Чистая отрасль – это условное понятие – некоторая часть народного хозяйства, более или менее цельная. Такими отраслями могут служить энергетика, машиностроение, станкостроение, приборостроение, сельское хозяйство и т.д.

Каждая отрасль выпускает некоторый продукт, часть которого потребляется другими отраслями (промежуточный продукт), а другая часть идет на конечное потребление и накопление (конечный продукт).

Обозначим через – валовый продукт -й отрасли, ; – стоимость продукта, произведенного в -й отрасли и потребленного в -й отрасли для изготовления продукции стоимостью ; – конечный продукт -й отрасли, – условно-чистая продукция -й отрасли, .

Рассмотрим основные соотношения межотраслевого баланса. Валовая продукция -й производящей отрасли () равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:

, . (1)

Коэффициент прямых затрат показывает, какое количество продукции -й отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции -й отрасли:

, , . (2)

Числа характеризуют технологию -й отрасли. С учетом формулы (1.2) систему уравнений баланса можно переписать в виде

, . (3)

Если ввести в рассмотрение матрицу коэффициентов прямых затрат , вектор-столбец валовой продукции и вектор столбец конечной продукции , то экономико-математическая модель межотраслевого баланса примет вид

. (4)

Модель межотраслевого баланса часто называют моделью В. Леонтьева или моделью «затраты-выпуск».

Заметим, что вывод уравнения (4) основан на двух важных допущениях. Первое допущение состоит в неизменности сложившейся технологии производства, когда элементы матрицы постоянны. Второе допущение состоит в предположении линейности существующих технологий, т.е. для выпуска -й отраслью продукции объема требуется ресурсов (продукции -й отрасли) в количестве единиц.

Важным вопросом в рассматриваемой модели является вопрос о существовании решения уравнения (4). Разумеется, с учетом экономической интерпретации вектор производства должен быть неотрицательным. Поэтому говорят, что модель Леонтьева продуктивна, если уравнение (4) имеет неотрицательное решение для любого , т.е. матрица коэффициентов прямых затрат позволяет произвести любой неотрицательный вектор потребления.

Теорема. Модель Леонтьева с матрицей продуктивна тогда и только тогда, если существует неотрицательная матрица, обратная к матрице , где – единичная матрица.

Можно доказать также, что модель Леонтьева продуктивна, если она позволяет произвести хоть какой-нибудь строго положительный вектор потребления; из этого вытекает, что можно произвести и любой неотрицательный вектор потребления.

Одним из признаков продуктивности матрицы является следующий: если сумма элементов столбцов (строк) матрицы не превосходит единицы, причем хотя бы для одного из столбцов (одной из строк) сумма элементов строго меньше единицы, то матрица продуктивна.

Из (4) следует, что

откуда

. (5)

Обозначим обратную матрицу как . Тогда . Это значит, что для любой -й отрасли справедливо соотношение:

, . (6)

Коэффициент полных затрат показывает, какое количество продукции -й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции -й отрасли. Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.

С помощью модели межотраслевого баланса можно выполнять три варианта расчетов:

1. Определить объем конечной продукции каждой отрасли, зная величины валовой продукции каждой отрасли:

2. Определить величины валовой продукции каждой отрасли, зная величины конечной продукции каждой отрасли:

3. Определить величины конечной продукции ряда отраслей и объемы валовой продукции остальных отраслей, зная величины валовой продукции первых отраслей и объемы конечной продукции остальных отраслей.

Валовая продукция -й потребляющей отрасли равна сумме ее материальных затрат и условно чистой продукции :

, . (7)

Межотраслевой баланс можно представить в таблице 1.

Таблица 1

Производящие отрасли	Потребляющие отрасли				Конечный продукт	Валовый продукт
Производящие отрасли	1	2	...	n	Конечный продукт	Валовый продукт
1			...
2			...
...	...	...	...	...	...	...
n			...
Условно-чистая продукция			...
Валовый продукт			...

Он состоит из четырех квадрантов. Первый квадрант (светло-бирюзовый) отражает межотраслевые потоки продукции. Второй (бледно-зеленый) характеризует отраслевую материальную структуру национального дохода. Третий (светло-желтый) представляет национальный доход как стоимость условно-чистой продукции. Четвертый квадрант (светло-коричневый) показывает конечное распределение и использование национального дохода.

Основной недостаток статической модели межотраслевого баланса состоит в том, что она не позволяет установить связи между планами производства отраслей и планами капитальных вложений, обеспечивающих развитие этих отраслей, т.е. модель не учитывает динамику самой экономики.

Задание 1. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

, .

Требуется составить межотраслевой баланс. С этой целью необходимо

- определить продуктивность модели;

- найти коэффициенты полных материальных затрат;

- определить вектор валовой продукции;

- вычислить межотраслевые потоки продукции;

- определить условно-чистую продукцию каждой отрасли;

- представить полученную информацию в виде межотраслевого баланса

производства и распределения продукции;

- изобразить диаграммы производства и потребления продукции для

различных отраслей.

Выполним расчеты, необходимые для составления межотраслевого баланса.

1. Продуктивность модели

Просуммируем элементы каждой строки матрицы . Получим

0,3 + 0,1 + 0,4 = 0,8;

0,2 + 0,5 = 0,7;

0,3 + 0,1 + 0,2 = 0,6.

Поскольку суммы элементов каждой строки меньше единицы, то модель межотраслевого баланса продуктивна.

2. Коэффициенты полных материальных затрат

Определим коэффициенты полных материальных затрат.

Находим матрицу :

Вычислим обратную матрицу , используя известные методы высшей математики. Получим

3. Вектор валовой продукции

Определим величины валовой продукции трех отраслей, используя процедуру умножения матрицы на вектор:

4. Матрица межотраслевых потоков продукции

Для определения элементов матрицы межотраслевых потоков продукции воспользуемся формулой

, , ,

вытекающей из (1.2). Тогда получим

;

5. Вектор условно-чистой продукции

Из (7) следует, что условно-чистая продукция -й потребляющей отрасли равна разности валовой продукции за вычетом суммы ее материальных затрат, т.е. , .

Тогда находим компоненты вектора условно-чистой продукции :

;

6. Расчеты в Excel

В таблице 2 показан один из возможных вариантов заполнения листа Excel и использования необходимых процедур для составления межотраслевого баланса.

Таблица 2

	A	B	C	D	E		F	G		H	I			J		K	L		M
1	E				A - матрица прямых материальных затрат						E-A
2	1	0	0		0,3	0,1			0,4			0,7	-0,1		-0,4
3	0	1	0		0,2	0,5			0			-0,2	0,5		0
4	0	0	1		0,3	0,1			0,2			-0,3	-0,1		0,8
5
6					Матрица межотраслевых потоков продукции						B = (E-A)^-1						Y		X
7					232,653	51,020			291,837			2,041	0,612		1,020			200	775,510
8					155,102	255,102			0,000			0,816	2,245		0,408			100	510,204
9					232,653	51,020			145,918			0,867	0,510		1,684			300	729,592
10
11				Z	155,102	153,061			291,837
12				X	775,510	510,204			729,592

Приведем последовательность вычислений:

1. В блок ячеек A2 : C4 помещается единичная матрица E. В блок ячеек E2 : G4 помещаются коэффициенты матрицы прямых материальных затрат A.

2. Матрица E – A рассчитывается в блоке I2 : K4 следующим образом: в ячейку I2 помещается формулу

= A2 – E2, которая протягивается на весь блок I2 : K4.

3. Для вычисления обратной матрицы выделяется блок ячеек I7 : K9, вызывается функция

и нажимается комбинация трех клавиш: CTRL + SHIFT + ENTER.

4. В блок ячеек L7 : L9 вводятся компоненты вектора конечной продукции Y.

5. В блоке ячеек M7 : M9 рассчитываются компоненты вектора валовой продукции X. Для этого выделяется указанный блок и используется функция

и нажимается комбинация трех клавиш: CTRL + SHIFT + ENTER.

6. В блок ячеек E12 : G12 переписываются компоненты ветора валовой продукции X. При этом можно выделить указанный блок, применить функцию транспонирования

и нажать комбинацию трех клавиш: CTRL + SHIFT + ENTER.

7. Блок ячеек E7 : G9 предназначен для расчета межотраслевых потоков продукции. Для этого в ячейку E7 записывается формула

= E2 * E$12, которая протягивается на указанный блок.

8. В ячейках блока E11 : G11 вычисляются значения условно-чистой продукции. Для этого в ячейку E11 помещается формула

, которая протягивается на ячейки указанного блока.

7. Межотраслевой баланс

Составим межотраслевой баланс производства и распределения продукции и поместим его в таблицу 3.

Таблица 3

	A	B	C	D	E	F
1	Производя-щие отрасли	Потребляющие отрасли			Конечный продукт	Валовый продукт
2	Производя-щие отрасли	1	2	3	Конечный продукт	Валовый продукт
3	1	232,7	51,02	291,8	200	775,5
4	2	155,1	255,1	0	100	510,2
5	3	232,7	51,02	145,9	300	729,6
6	Условно-чистая продукция	155,1	153,1	291,8	600
7	Валовый продукт	775,5	510,2	729,6		2015,3

В первом квадранте светло-бирюзового цвета помещаются межотраслевые потоки продукции. Во втором квадранте бледно-зеленого цвета помещаются конечный и валовый доход. В третьем светло-желтом квадранте помещаются условно-чистая продукция и валовый доход. В четвертом светло-коричневом квадранте помещаются суммарные значения по всем отраслям конечного и валового продукта.

На рис. 1 представлена диаграмма распределения продукции каждой производящей отрасли по потребляющим отраслям с учетом конечного продукта. Для построения диаграммы следует выделить блок ячеек B3 : E5 и выбрать линейчатую диаграмму с накоплением, поменяв при этом строки со столбцами.

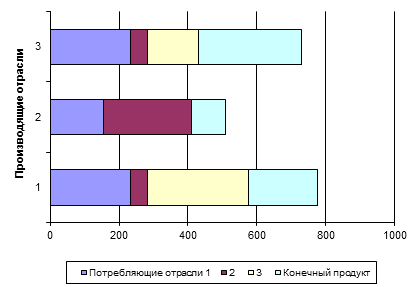
Рис. 1. Распределение продукции для каждой производящей отрасли

На рис. 2. представлена диаграмма потребления продукции каждой отраслью с учетом условно-чистого продукта. Для построения этой диаграммы выделяется блок ячеек B3:D6, выбирается столбиковая гистограмма с накоплением и меняются строки со столбцами.

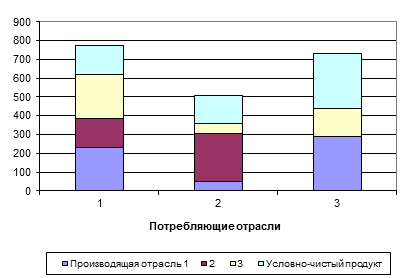
Рис. 2. Потребление продукции каждой отраслью

Лабораторная работа №8. Производственные функции: оценка параметров ПФ Кобба-Дугласа

Модели производственно-технологического уровня служат основой для анализа функционирования и прогнозирования развития различных хозяйственных единиц как на микроуровне (предприятие, фирма, монополия и т.д.), так и на макроуровне (отрасль, межотраслевой комплекс, регион, народное хозяйство страны в целом).

Одним из наиболее распространенных подходов к моделированию производственного процесса является рассмотрение его как открытой системы, входами которой служат затраты ресурсов, а выходами объем продукции, выраженный в натуральном или денежном выражении.

При использовании такого подхода в макроэкономике особое распространение получили производственные функции, у которых все компоненты выпуска (по стоимости или в натуральном выражении) объединены в одну скалярную величину (Y), а число разнородных производственных ресурсов (факторы Xj) сведено к минимуму, допускающему расчет параметров производственной функции на базе имеющейся информации: Y = F(Xi,X2,...,X_N).

Эта производственная функция представляет собой регрессионную модель, поскольку связь между затратами и выпуском носит статистический характер.

При нахождении значений параметров производственной функции вместе с их расчетом определяются границы изменения независимых величин, при которых корректно применение модели. Подчеркнем, что производственные функции могут быть построены для различных производственных единиц: предприятия, отрасли, народного хозяйства в целом. Степень агрегирования переменных может быть также различной – от номенклатуры деталей до обобщенных показателей народного хозяйства.

Особое значение имеют двухфакторные производственные функции:

Y=F(K,L), (1)

где Y - объем выпуска продукции,

L - затраты труда,

К - затраты капитала (объем основных промышленно-производст-венных фондов).

Первый успешный опыт построения производственных функций на базе статистических данных был осуществлен американскими экономистами Ч. Коббом и П. Дугласом (1929 г.). При анализе статистических данных обрабатывающей промышленности США они обнаружили, что связь между производительностью труда Y/L и фондовооруженностью K/L хорошо описывается степенной зависимостью Y/L - q(K/L)^a, где а >0 - постоянное число. Из этого уравнения формально следует соотноше-ние Y = qK^aL^{1-а ,} в котором переменные К и L можно рассматривать как независимые факторы, влияющие на объем производства.

Производственная функция Кобба - Дугласа в общем случае имеет следующий вид:

Y=AK^aL^b, (2) , где а>0, b>0.

Производственные функции позволяют получить ответ на вопрос о том, как изменится объем производства, если все затраты изменяются в одной и той же пропорции.

Пример. Пусть уровень производства определяется в соответствии с функцией Кобба - Дугласа.

Если факторы производства изменятся в λ раз и примут значения соответственно λК и λL, то значение выпуска составит

B(λК)^a(λL)^b=Bλ^a+b К^aL^b=λ^a+bY

Как видим, выпуск изменится в λ^a⁺^b раз. Это значит, что если а + b =1, то пропорциональное увеличение обоих затрачиваемых ресурсов приводит к росту выпуска в той же пропорции. Такое изменение в экономической литературе литературе называют постоянным эффектом масштаба.

Если a+b<1, то рост выпуска продукции, вызванный пропорциональным увеличением обоих затрачиваемых ресурсов, происходит в меньшей степени, чем рост ресурсов (в этом случае говорят об отрицательном эффекте масштаба).

Если же а+b>1, то рост выпуска продукции, вызванный пропорциональным увеличением обоих затрачиваемых ресурсов, происходит в большей степени, чем рост ресурсов (в этом случае говорят о положительном эффекте масштаба).

Это свойство производственной функции Кобба-Дугласа (2) связано с тем, что она является однородной, функцией степени а+b.Поэтому производственная функция Кобба-I Дугласа(2) в случае а + b = 1 иазывается линейно-однородной.

Задание 1. В таблице приведены значения объема выпуска для различных значений затрат ресурсов

L K	50	60	70	80
10	31,518	35,162	38,569	41,786
20	41,589	46,396	50,892	55,138
30	48,912	54,566	59,854	64,846
40	54,877	61,220	67,153	72,754

Найти параметры ПФКД:

Решение: Поиск параметров можно выполнить путем проведения многомерной регрессии между объемом производства и затратами ресурсов.

Для этого предварительно логарифмируем исходные данные, что эквивалентно переходу от нелинейной ПФ к линейной

В таблице 2 представлены промежуточные расчеты для построения модели.

Таблица 2

Таблица для расчета параметров производственной функции Кобба-Дугласа

Y	K	L	ln Y	ln K	ln L
31,518	10	50	3,451	2,303	3,912
35,162	10	60	3,560	2,303	4,094
38,569	10	70	3,652	2,303	4,248
41,786	10	80	3,733	2,303	4,382
41,589	20	50	3,728	2,996	3,912
46,396	20	60	3,837	2,996	4,094
50,892	20	70	3,930	2,996	4,248
55,138	20	80	4,010	2,996	4,382
48,912	30	50	3,890	3,401	3,912
54,566	30	60	3,999	3,401	4,094
59,854	30	70	4,092	3,401	4,248
64,846	30	80	4,172	3,401	4,382
54,877	40	50	4,005	3,689	3,912
61,22	40	60	4,114	3,689	4,094
67,153	40	70	4,207	3,689	4,248
72,754	40	80	4,287	3,689	4,382

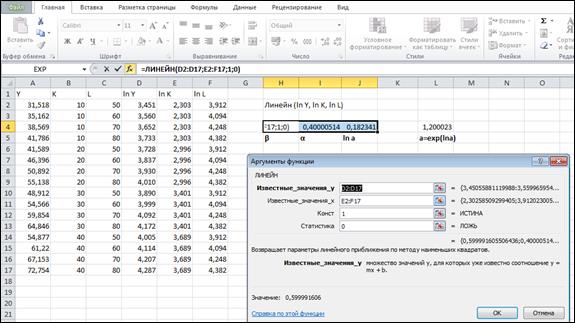
Рис.1. Окно расчета параметров производственной функции Кобба-Дугласа

Таким образом, ПФКД имеет вид: .

Лабораторные работы № 9-11.

Моделирование динамики экономической системы

(Производственные функции. Модель Солоу)

Задание 1. Известны динамические ряды по валовому региональному продукту (ВРП), млрд. руб., среднегодовой численности занятых в экономике, тыс. чел., основным фондам в экономике (ОФ), млрд. руб. Центрального федерального округа РФ за период с 2002 по 2015 гг., которые представлены в таблице 1.

Таблица 1

Некоторые социально-экономические показатели регионов ЦФО за 2003 – 2015 гг.

	ВРП, млрд. руб.	ОФ, млрд. руб.	числ., тыс. чел.
2003	3227,9	6296,1	17619,1
2004	3939,6	8304,2	17735,5
2005	4586,8	9280	18220,4
2006	6157,2	11481,9	18357,4
2007	7849,7	13199,9	18464,9
2008	10305,2	18409,5	18732,1
2009	12927,6	25151	19016,9
2010	11445,2	26617	18567,8
2011	13363,6	30674	18619,2
2012	16170,5	34971	18710,3
2013	17433,1	38981	18814,1
2014	18975,9	43532	18894,7
2015	20820,6	47271	19008,3

Необходимо

- определить параметры и сформировать производственную функцию Кобба-Дугласа с учетом технического прогресса;

- рассчитать ВВП на основе модели производственной функции, сравнить фактические данные ВВП с данными, полученными по модели, результаты сравнения оформить таблицей и графиками;

- рассчитать ВВП на основе модели производственной функции при условии отсутствия технического прогресса, сравнить фактические данные ВВП с данными, полученными по модели при отсутствии технического прогресса, результаты оформить таблицей и графиками;

- провести оценку основных характеристик производственной функции – эффективность капитала и труда, предельной нормы замещения;

- построить модель экономической динамики, взяв за основу модель Солоу с линейным и экспоненциальным изменением нормы накопления, рассчитать основные и дополнительные показатели модели;

- изобразить графики динамики основных и дополнительных показателей, полученных в результате проведенных расчетов.

1. Оценка основных характеристик производственной функции

Зная производственную функцию, можно рассчитать ряд числовых характеристик. Рассмотрим основные из них.

1. Средней производительностью по каждому ресурсу называются величины:

, , которые имеют смысл среднего выпуска продукции из расчета единичных затрат данного ресурса.

Если – материальные затраты, а – трудовые, то называется капиталоотдачей, а называется производительностью труда.

2. Предельной или маржинальной производительностью по каждому ресурсу называются величины:

, .

Эти величины показывают приближённо, насколько единиц изменится выпуск, если затраты того или иного ресурса изменятся на единицу:

, .

3. Частной эластичностью по каждому ресурсу называются величины:

, .

Эластичности приближенно показывают, насколько процентов изменится выпуск, если затраты того или иного ресурса изменятся на один процент:

, .

Величина называется полной эластичностью или эластичностью производства.

4. Технологической нормой замены называется величина , которая приближенно показывает, как изменится выпуск, если единицу одного ресурса заменить единицей другого.

На практике при моделировании реальных производств чаще всего используют два вида производственных функций: линейную и Кобба-Дугласа.

Линейная производственная функция имеет вид:

Она строится в случаях, когда объем выпуска пропорционален затратам. Однако данная функция не удовлетворяет первому и третьему требованиям к производственным функциям, поэтому ее можно использовать для приближения реальных функций на небольших локальных участках изменения их аргументов. Для выполнения второго требования необходимо выполнение условий , .

Производственная функция Кобба-Дугласа имеет вид:

(1)
Для выполнения всех требований к производственным функциям необходимо выполнение условий:

, , . (2)

Найдем средние и предельные производительности, эластичности, технологическую норму замены для линейной и Кобба-Дугласа производственных функций.

Для линейной функции будет:

, ;

, ,

, .

Таким образом, коэффициенты и линейной производственной функции имеют смысл предельных производительностей и их можно вычислять по формулам:

, . (3)

Для производственной функции Кобба-Дугласа будет:

, ;

, , ;

Таким образом, коэффициенты и производственной функции Кобба-Дугласа имеют смысл частных эластичностей и их можно вычислять по формулам:

, . (4)

2. Модель экономического роста Солоу

Производственная функция Кобба-Дугласа обычно записывается в виде

, где

– выпуск продукции,

– производственный коэффициент,

– объем используемого капитала,

– затраты живого труда.

Неоклассическая модель экономического роста Роберта Солоу основывается на производственной функции Кобба-Дугласа. Основное отличие модели Солоу от производственной функции заключается в том, что в уравнение вводится технический прогресс как фактор экономического роста наравне с такими факторами производства как труд и капитал.

Величина технического прогресса зависит от времени и вводится в производственную функцию в виде сомножителя , где величина характеризует степень технического прогресса, а величина – время, прошедшее с начала процесса прогнозирования. Тогда производственная функция представляется в виде

Модель описывает влияние трех вышеупомянутых факторов на экономический рост и описывается мультипликативной производственной функцией, составляющей основу модели, и рядом условий и ограничений.

Под техническим прогрессом в данной модели подразумевается вся совокупность качественных изменений труда и капитала. Таким образом, показатель технического прогресса является показателем времени. Технический прогресс является нейтральным, так как он одинаково влияет на все задействованные для выпуска продукции ресурсы.

При технический прогресс отсутствует, и мы получаем производственную функцию Кобба-Дугласа.

3. Показатели, характеризующие динамику производственной системы

С учетом развития системы производственная функция в год характеризуется уравнением, содержащим явную зависимость показателей от времени:

. (6)

Наряду с такими показателями, как капитал , труд и выпуск продукции к основным показателям относятся также фонд накопления и фонд потребления . Эти фонды зависят от нормы накопления за время . Обычно рассматривается линейная или экспоненциальная политика изменения нормы накопления, которые имеют вид

(7)

или

(8)

соответственно. Здесь и – некоторые постоянные параметры, характеризующие величину нормы накопления.

Фонд накопления равен произведению нормы накопления на значение производственной функции :

. (9)

Фонд потребления равен разности между значением производственной функции и фондом накопления

. (10)

К дополнительным показателям относятся:

- фондовооруженность труда ,

- производительность труда ,

- отдача капитала ,

- среднедушевое потребление .

Указанные основные и дополнительные показатели на каждый год прогнозируемого периода рассчитываются рекуррентно на основе соотношений (7) - (10), а также формул для дополнительных показателей.

Выполнение работы

Динамические ряды по валовому региональному продукту (ВРП), млрд. руб., среднегодовой численности занятых в экономике, тыс. чел., основным фондам в экономике (ОФ), млрд. руб. Центрального федерального округа РФ за период с 2002 по 2015 гг. представлены в таблице 1.

Допустим, что постоянные параметры, характеризующие норму накопления, равны и соответственно.

Определение параметров и формирование производственной функции

Данные из таблицы 1 поместим на лист Excel в блок ячеек A2 : D14, как показано на рис.2.

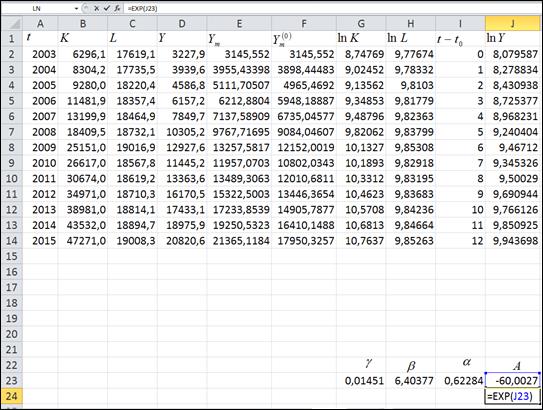
Рис.2. Рабочий лист расчета параметров производственной функции Кобба-Дугласа

Производственную функцию Кобба-Дугласа с учетом технического прогресса (модель Солоу) будем искать в виде уравнения

с неизвестными параметрами , , , . Логарифмируя эту функцию, получим

(11) .

Из равенства (11) следует, что значения функции линейно зависят от значений , и . Поэтому коэффициенты , , и уравнения (11) можно определить в Excel с помощью процедуры =ЛИНЕЙН().

Колонки E и F (рис. 2.) временно оставим пустыми. Дополним колонками G, H, I, J, в которые поместим значения величин , , и , входящих в соотношение (11). Для применения процедуры =ЛИНЕЙН() на свободном месте листа Excel выделим блок ячеек из одной строки и 4 столбцов. Затем в списке функций находим процедуру = ЛИНЕЙН(). На экране появляется окно, в поля которого надо ввести 4 аргумента:

- одномерный массив значений результирующего фактора (отклика) ;

- двумерный массив значений факторов , , ;

- значение ИСТИНА (или число 1), так как в уравнении присутствует свободный член;

- значение ЛОЖЬ (или число 0), поскольку требуется вычислить лишь коэффициенты уравнения регрессии.

Одновременное нажатие трех клавиш «Ctrl» + «Shift» + «Enter» приводит к появлению коэффициентов уравнения (11) в ячейках выделенного блока.

Выделим, например, блок ячеек G23 : J23 и запишем функцию =ЛИНЕЙН с необходимыми аргументами. Тогда для исходных данных таблицы 1 в командной строке будет находиться выражение

{=ЛИНЕЙН(J2 : J14; G2 : I14; 1; 0)}, а результаты расчетов отображаются на рис. 2.

В блоке ячеек G23 : J23 содержатся коэффициенты уравнения линейной зависимости (11) в обратном порядке.

В ячейке J24 вычислим параметр в соответствии с формулой

= EXP(J23).

Подставим параметры в уравнение производственной функции

(12)

При отсутствии технического прогресса получим следующее уравнение производственной функции

(13) .

Расчет ВВП по модели в условиях наличия и отсутствия технического прогресса

Рассчитаем ВВП на основе модели производственной функции (12) и сравним их с фактическими данными ВВП. В ячейку E2 поместим формулу

= $J$24 * СТЕПЕНЬ(B2; $I$23) * СТЕПЕНЬ(C2; $H$23) * EXP($G$23 * (A2 - $A$2)), которую протянем на блок ячеек E3 : E14. В колонке E будут содержаться значения ВВП, полученные по модели производственной функции в условиях технического прогресса.

Аналогично в колонке F согласно (13) рассчитываются значения ВВП при условии отсутствия технического прогресса. Для этого ячейку F2 помещается формула

= $J$24 * СТЕПЕНЬ(B2; $I$23) * СТЕПЕНЬ(C2; $H$23), которая протягивается на блок ячеек F3 : F14.

Из рис. 2 следует, что значения ВВП, полученные по математической модели (колонка E) хорошо согласуются с фактическими значениями (колонка D). На графике (рис. 3) эти две кривые неразличимы. Существенное различие в значениях и на графике наблюдается при сравнении ВВП с учетом и без учета технического прогресса (колонка F).

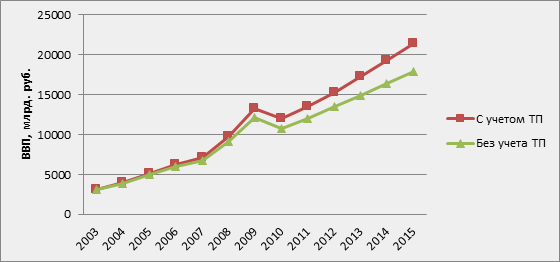
Рис. 3. Динамика значений ВВП с учетом и без учета технического прогресса, полученная с помощью производственной функции Кобба-Дугласа по данным регионов ЦФО за 2003 – 2015 гг.

Видим, что технический прогресс дает значительное увеличение ВВП начиная с 2007 г.

Основные характеристики производственной функции

Проведем оценку основных характеристик производственной функции – эффективность капитала и труда, эластичности и предельной нормы замещения. Характеристиками производственной функции Кобба-Дугласа являются:

- средние производительности по капиталу и труду:

, ;

- предельные производительности по капиталу и труду:

, ;

- частные и общая эластичности:

, , ;

- технологическая норма замены

В соответствии с приведенными формулами необходимо вычислить значения указанных характеристик.

На рисунке 4 представлен фрагмент рабочего окна расчета основных характеристик производственной функции.

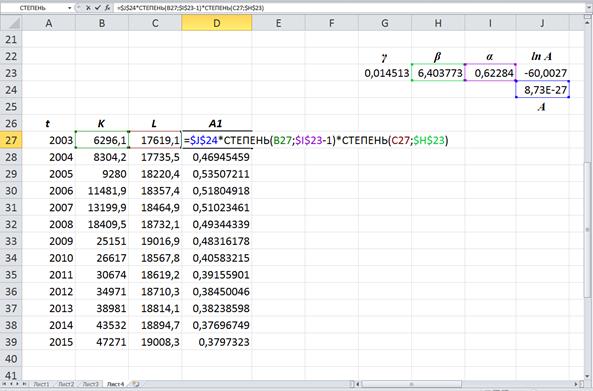
Рис. 4. Фрагмент окна расчета основных характеристик производственной функции

Модель экономической динамики

Построим модель экономической динамики, взяв за основу модель Солоу с линейным и экспоненциальным изменением нормы накопления. Основные и дополнительные показатели модели определим на основе формул п. 3.

На листе Excel с именем «Модель» составим таблицу, как это показано на рисунке 5, соответствующая линейной и экспоненциальной политике изменения нормы накопления. В первом случае расчет нормы накопления ведется по формуле (7), а во-втором – по формуле (8). Допустим,

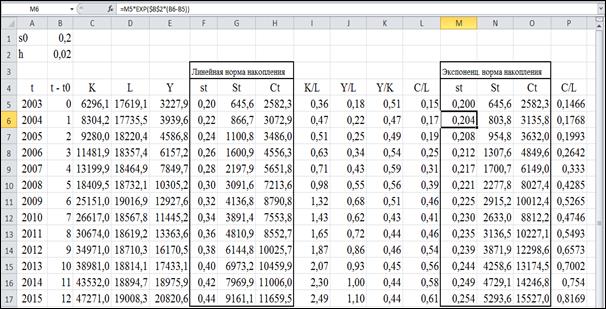
Рис.5. Рабочее окно расчета основных и дополнительных показателей модели Солоу

Таблица 2

Основные и дополнительные показатели модели Солоу при линейной и экспоненциальной политике изменения нормы накопления

t	Линейная норма накопления			K/L	Y/L	Y/K	C/L	Экспон. норма накопления
t	s_t	S_t	C_t	K/L	Y/L	Y/K	C/L	s_t	S_t	C_t
2003	0,20	645,6	2582,3	0,36	0,18	0,51	0,15	0,200	645,6	2582,3
2004	0,22	866,7	3072,9	0,47	0,22	0,47	0,17	0,204	803,8	3135,8
2005	0,24	1100,8	3486,0	0,51	0,25	0,49	0,19	0,208	954,8	3632,0
2006	0,26	1600,9	4556,3	0,63	0,34	0,54	0,25	0,212	1307,6	4849,6
2007	0,28	2197,9	5651,8	0,71	0,43	0,59	0,31	0,217	1700,7	6149,0
2008	0,30	3091,6	7213,6	0,98	0,55	0,56	0,39	0,221	2277,8	8027,4
2009	0,32	4136,8	8790,8	1,32	0,68	0,51	0,46	0,225	2915,2	10012,4
2010	0,34	3891,4	7553,8	1,43	0,62	0,43	0,41	0,230	2633,0	8812,2
2011	0,36	4810,9	8552,7	1,65	0,72	0,44	0,46	0,235	3136,5	10227,1
2012	0,38	6144,8	10025,7	1,87	0,86	0,46	0,54	0,239	3871,9	12298,6
2013	0,40	6973,2	10459,9	2,07	0,93	0,45	0,56	0,244	4258,6	13174,5
2014	0,42	7969,9	11006,0	2,30	1,00	0,44	0,58	0,249	4729,1	14246,8
2015	0,44	9161,1	11659,5	2,49	1,10	0,44	0,61	0,254	5293,6	15527,0

Значения величин и в колонках G и H характеризуют фонды накопления и потребления соответственно; они рассчитываются по формулам (9) и (10). В колонках I, J, K, L содержатся значения дополнительных параметров модели динамики: фондовооруженность, производительность труда, отдача капитала, среднедушевое потребление.

Изобразим графики динамики основных и дополнительных показателей, полученных в результате проведенных расчетов. На рис. 2.2 представлено изменение фондов накопления и потребления. Фонд накопления растет достаточно быстро, в то время как фонд потребления убывает.

Критерием успешности развития экономики является показатель среднедушевого (удельного) потребления. На рис. 6 приведены графики среднедушевого потребления для различных политик нормы накопления.

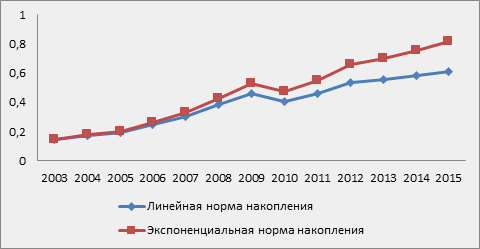
Рис. 6. Динамика среднедушевого потребления

Видим, что среднедушевое потребление выше для экспоненциальной политики нормы потребления c 2007 г. При этом с течением времени этот показатель возрастает.

Содержание отчета по работе

Отчет должен содержать следующие пункты:

- задание на работу с конкретными исходными данными студента;

- параметры и производственную функцию Кобба-Дугласа с учетом технического прогресса;

- расчет ВВП на основе модели производственной функции, сравнение фактических данных ВВП с данными, полученными по модели, привести соответствующие графики;

- расчет ВВП на основе модели производственной функции при условии отсутствия технического прогресса, сравнить фактических данных ВВП с данными, полученными по модели при отсутствии технического прогресса, результаты отобразить на графиках;

- оценку основных характеристик производственной функции – эффективность капитала и труда, предельной нормы замещения;

- модель экономической динамики, взяв за основу модель Солоу с линейным и экспоненциальным изменением нормы накопления, расчет основных и дополнительных показателей модели;

- графики динамики основных и дополнительных показателей, полученных в результате проведенных расчетов;

- выводы по работе.

Лабораторная работа №12. Экономико-математическая модель международной торговли (линейная модель обмена). Моделирование средствами Excel

Задание. Найти национальные доходы четырех торгующих стран в сбалансированной системе международной торговли, если структурная матрица торговли этих четырех стран равна

а сумма бюджетов стран не превышает 7680 млн.ден.ед.

Математическая модель

при ограничениях:

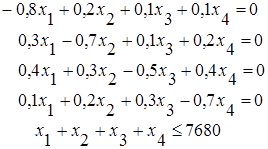
Решение задачи средствами Excel

Задание исходных данных на рабочем листе Excel приведено на рис.1.

Рис. 1. Исходные данные в Excel

В ячейки В2:Е6 занесены коэффициенты при системе ограничений, в ячейках G2:G6 содержатся ограничения в правых частях, в ячейки I2:I6 занесены формулы левых частей ограничений, ячейки В9:Е9 содержат изменяемые переменные . Например, в ячейке I2 записана формула ограничений =СУММПРОИЗВ(В2:Е2;В9:Е9). Аналогичные формулы записаны в ячейках I3:I6. Формула целевой функции =СУММ(В9:Е9) занесена в ячейку С10.

Рис. 2. Решение задачи средствами Excel

Процесс решения – занесение в окно «Поиск решения» ячейки с формулой целевой функции, занесение изменяемых ячеек, внесение ограничений приведено на рис. 2. В окне «Параметры» необходимо отметить: «Линейная модель», «Неотрицательные значения», «Автоматическое масштабирование».

На рис. 2 приведены также результаты решения, согласно которым национальные доходы четырех стран равны соответственно 1015.359, 1458.228, 3251.308, 1955.105 млн. ден.ед. Из содержимого ячеек I2:I6 видно, что все ограничения выполнены. Значение целевой функции (ячейка С10) равно 7680 млн.ден.ед.

Список использованной литературы

1. Адамадзиев К. Р., Джаватов Д.К., Абдуллаев Г.Ш. Экономико-математические методы и модели. – Махачкала: Изд.-полиграф. центр ДГУ, 2003. – 109 с.

2. Адамадзиев К.Р., Касимова Т.М. Имитационная модель производства сельскохозяйственной продукции. Материалы одиннадцатой региональной научно-практической конференции «Компьютерные технологии в науке, экономике и образовании / Под ред. проф. К.Р. Адамадзиева. – Махачкала: ИПЦ ДГУ, 2010. – С. 80-85.

3. Адамадзиев К.Р., Халилов М.А. Модели производственных функций регионов: расчет параметров и характеристик, анализ зависимости выпуска продукции от затрат // Фундаментальные исследования. – 2016. – № 4-2.–С.339-345; URL: https://fundamental-research.ru/ru/article/view?id=40178 (дата обращения: 25.02.2017).

4. Беляева М. А. Имитационное моделирование социально-экономических систем для поддержки принятия решений // Пищевая промышленность. – 2011. - №4.

5. Гуров С.В. Математическая экономика: Методические указания по выполнению лабораторных работ для студентов специальности 080100 «Экономика» всех форм обучения. - Санкт-Петербург: Санкт-Петербургский государственный лесотехнический университет, 2014. – 73 с.

6. Емельянов А.А. и др. Имитационное моделирование экономических процессов: Учебное пособие. – М.: Финансы и статистика, 2002. – 368 с.

7. Замков О.О. Математические методы в экономике: Учебник. – Изд. 5-ое испр. – М.: Дело и Сервис, 2009. – 384 с.

8. Имитационное моделирование : сборник лабораторных работ для студентов очной формы обучения по направлению 080800.62 «Приклад- ная информатика», квалификации «Бакалавр прикладной информатики» / сост. Т.В. Маколкина ; АлтГАКИ, каф. информатики. – Барнаул : Изд-во АлтГАКИ, 2011. – 36 с.

9. Касимова Т.М. Анализ показателей деятельности предприятий аграрного сектора с помощью экономико-математических моделей. // Вестник Российской экономической академии им. Г. В. Плеханова. – 2011. №3. – С. 114-118.

10. Кузнецов Ю.А. Мичасова О.В. Теоретические основы имитационного и компьютерного моделирования экономических систем: Учебно-методическое пособие. - Нижний Новгород: Издательство Нижегородского госуниверситета, 2007.

11. Мичасова О.В. Имитационное моделирование экономических: Учебно-методическое пособие. – Нижний Новгород: Нижегородский госуниверситет, 2014. – 186 с.

12. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – М.: Вузовский учебник, 2004

13. Эконометрика: учебник / Под ред. В. С. Мхитаряна. – М.: Проспект, 2009. – 384 с.

14. Эконометрика: учебник / Под. ред. И.И. Елисеевой. – М.: Финансы и статистика, 2005. – 576 с.