Проведение статистического анализа данных с помощью вычислительных пакетов

Случайные величины

Нормальное (Гауссово) распределение

Равномерное распределение

Биномиальное распределение

Другие статистические распределения

Статистические характеристики. Построение гистограмм.

Среднее значение и дисперсия

Генерация коррелированных случайных чисел. Ковариация и корреляция.

Коэффициенты асимметрии и эксцесса. Другие статистические характеристики.

Случайные процессы

Случайные величины

Для моделирования различных физических, экономических и прочих эффектов широко распространены методы, называемые методами Монте-Карло. Их основная идея состоит в создании определенной последовательности случайных чисел, моделирующей тот или иной эффект, например, шум в физическом эксперименте, случайную динамику биржевых индексов и т. п. Для этих целей в Mathcad имеется ряд встроенных функций, реализующих различные типы генераторов псевдослучайных чисел.

Согласно определению, случайная величина принимает то или иное значение, но какое конкретно, зависит от случайных обстоятельств опыта и заранее точно предсказано быть не может. Можно лишь говорить о вероятности P(X^к) принятия случайной дискретной величиной того или иного значения хк, или о вероятности попадания непрерывной случайной величины в тот или иной числовой интервал (х,х+dх). Вероятность Р(Х^К) или P(X) (dх), соответственно, может принимать значения от о (такое значение случайной величины совершенно невероятно) до i (случайная величина заведомо примет значение от х до х+dх). Соотношение Р(Х_К) называют законом распределения случайной величины, а зависимость P(х) между возможными значениями непрерывной случайной величины и вероятностями попадания в их окрестность называется ее плотностью вероятности (probability density).

В Mathcad имеется ряд встроенных функций, задающих используемые в математической статистике законы распределения. Они вычисляют как значение плотности вероятности различных распределений по значению случайной величины х, так и некоторые сопутствующие функции. Все они, по сути, являются либо встроенными аналитическими зависимостями, либо специальными функциями. Большой интерес представляет наличие генераторов случайных чисел, создающих выборку псевдослучайных данных с соответствующим законом распределения.

Рассмотрим подробно возможности Mathcad на нескольких наиболее популярных законах распределения, а затем приведем перечень всех распределений, встроенных в Mathcad.

Нормальное (Гауссово) распределение

В теории вероятности доказано, что сумма различных независимых случайных слагаемых (независимо от их закона распределения) оказывается случайной величиной, распределенной согласно нормальному закону (т. н. центральная предельная теорема). Поэтому нормальное распределение хорошо моделирует самый широкий круг явлений, для которых известно, что на них влияют несколько независимых случайных факторов.

Перечислим встроенные функции, имеющиеся в Mathcad для описания нормального распределения вероятностей:

· dnorm(x,m,o) – плотность вероятности нормального распределения;

· рпогт(х,m,о) – функция нормального распределения;

· спогт(х) – функция нормального распределения для ц= о,o=i;

· дпогт(P,m,о) – обратная функция нормального распределения;

· гпогт(M,m,o) – вектор м независимых случайных чисел, каждое из которых имеет нормальное распределение;

o х – значение случайной величины;

o Р – значение вероятности;

o m– математическое ожидание;

o о – среднеквадратичное отклонение.

Математическое ожидание и дисперсия являются, по сути, параметрами распределения. Плотность распределения для трех пар значений параметров показана на рис. 1. Напомним, что плотность распределения dnorm задает вероятность попадания случайной величины х в малый интервал от х до х+dх. Таким образом, например, для первого графика (сплошная линия) вероятность того, что случайная величина х примет значение в окрестности нуля, приблизительно в три раза больше, чем вероятность того, что она примет значение в окрестности х=2. А значения случайной величины, большие 5 и меньшие -5, и вовсе маловероятны.

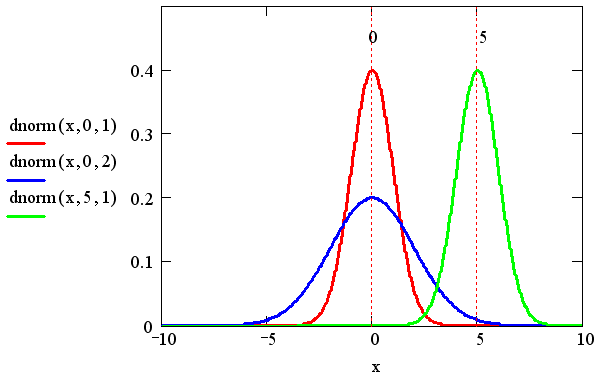
Рис. 1. Плотность вероятности нормальных распределений

Функция распределения F(X) (cumulative probability) – это вероятность того, что случайная величина примет значение меньшее или равное х. Как следует из математического смысла, она является интегралом от плотности вероятности в пределах от – x до х. Функции распределения для упомянутых нормальных законов изображены на рис. .2. Функция, обратная F(X) (inverse cumulative probability), называемая еще квантилем распределения, позволяет по заданному аргументу р определить значение х, причем случайная величина будет меньше или равна х с вероятностью р.

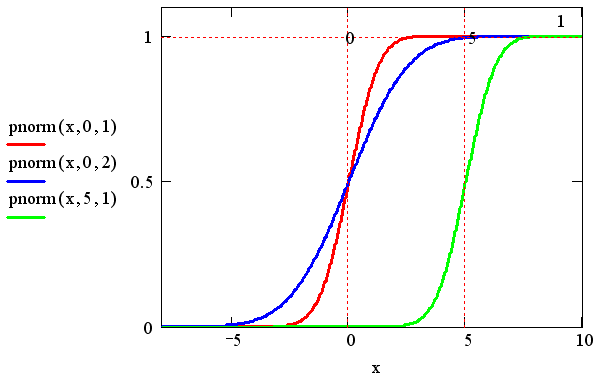
Рис. 2. Нормальные функции распределения

Здесь и далее графики различных статистических функций, показанные на рисунках, получены с помощью Mathcad без каких-либо дополнительных выражений в рабочей области.

Равномерное распределение

Самое простое распределение случайной величины – это распределение с постоянной вероятностью. Вероятность p=const=1/ (b-a) при хе(а,b) и P=0, для х вне интервала (а,b). Эту плотность вероятности, наряду с прочими статистическими характеристиками, задают следующие встроенные функции:

· dunif (x,a,b) – плотность вероятности равномерного распределения;

· punif(x,a,b) – функция равномерного распределения;

· qunif(p,a,b) – квантиль равномерного распределения;

· runif (м,а,b) – вектор м независимых случайных чисел, каждое из которых имеет равномерное распределение;

· rnd (x) – случайное число, имеющее равномерную плотность распределения на интервале (о, х);

o х – значение случайной величины;

o Р – значение вероятности;

o (а,b) – интервал, на котором случайная величина распределена равномерно.

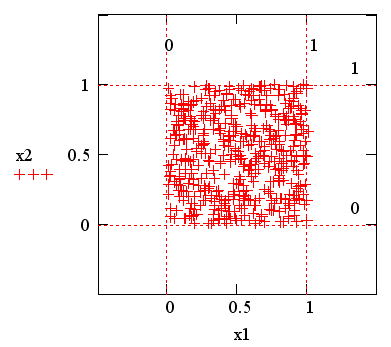
Рис. 14.3 Псевдослучайные числа с равномерным законом распределения

Чаще всего в несложных программах применяется последняя функция, которая приводит к генерации одного псевдослучайного числа. Наличие такой встроенной функции в Mathcad – дань традиции, применяемой в большинстве сред программирования. Пример использования генератора вектора из м случайных чисел показан на рис. 3, который получен заменой в двух последних строках листинга .7 генератора нормальных чисел на runif (м,0, 1). Плотность вероятности и функция равномерного распределения показаны на рис. 4.

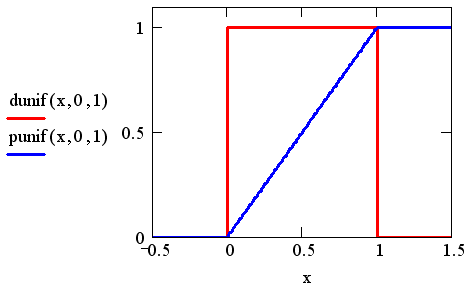
Рис. 4. Плотность вероятности и функция равномерного распределения

Биномиальное распределение

Приведем встроенные функции, описывающие еще одно распределение случайной величины, которая, в отличие от двух предыдущих, является не непрерывной, а может принимать лишь дискретные значения. Биномиальное распределение описывает последовательность независимых испытаний, каждое из которых может приводить к генерации определенного события с постоянной вероятностью р.

· dbinom(k,n,p) – плотность вероятности биномиального распределения (рис. 14.6);

· pbinom(k,n,p) – функция биномиального распределения;

· qbinom(P,n,p) – квантиль биномиального распределения;

· rbinom(M,n,р) – вектор м независимых случайных чисел, каждое из которых имеет биномиальное распределение;

o k – дискретное значение случайной величины;

o Р – значение вероятности;

o n– параметр распределения (количество независимых испытаний);

o р – параметр распределения (вероятность единичного случайного события).

Примером биномиального распределения может служить n-кратное подбрасывание монеты. Вероятность выпадения орла или решки в каждом испытании равна р=0.5, а суммарное количество выпадений, например орла, задается биномиальной плотностью вероятности. Приведем простой пример: если монета подбрасывалась 50 раз, то наиболее вероятное количество выпадений орла, как видно по максимуму плотности вероятности на рис. 5, составляет 25. Вероятность того, что орел выпадет 25 раз, составляет dbinom(25, 50, 0.5) =0.112, а, скажем, вероятность того, что 15 раз dbinom(15.50.0.5)=0.002.

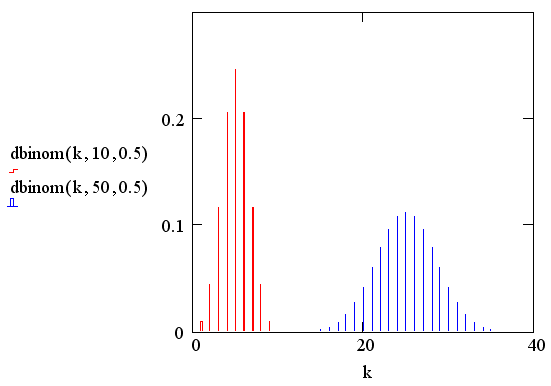
Рис. 5. Плотность вероятности биномиального распределения

Другие статистические распределения

Как легко заметить по рассмотренным трем распределениям, Mathcad имеет четыре основные категории встроенных функций. Они различаются написанием их первой литеры, а оставшаяся часть имени функций (ниже в списке функций она условно обозначена звездочкой) идентифицирует тот или иной тип распределения.

· d*(x,par) – плотность вероятности;

· р*(х,раг) – функция распределения;

· q*(p,par) – квантиль распределения;

· r* (м,раг) – вектор м независимых случайных чисел, каждое из которых имеет соответствующее распределение;

o х – значение случайной величины (аргумент функции);

o Р – значение вероятности;

o par – список параметров распределения.

Чтобы получить функции, относящиеся, например, к равномерному распределению, вместо * надо поставить unif и ввести соответствующий список параметров par. Он будет состоять в данном случае из двух чисел а,b – интервала распределения случайной величины.

Перечислим все типы распределения, реализованные в Mathcad, вместе с их параметрами, на этот раз обозначив звездочкой * недостающую первую букву встроенных функций. Некоторые из плотностей вероятности показаны на рис. 6.

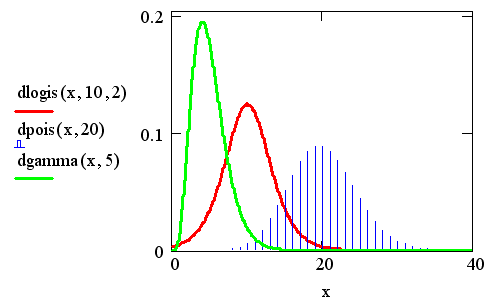
Рис. 6. Плотность вероятности некоторых распределений

· *beta(x,s1,s2) – бета-распределение (si,s2>o – параметры, o<x<i).

· *binom(k,n,p) – биномиальное распределение (n – целый параметр, 0<k<n и 0<р<1 – параметр, равный вероятности успеха единичного испытания).

· *cauchy(x,l,s) – распределение Коши (l – параметр разложения, s>0 – параметр масштаба).

· *chisq(x,d) – x² ("хи-квадрат") распределение (d>0 – число степеней свободы).

· *ехр(х,r) – экспоненциальное распределение (r>0 – показатель экспоненты).

· *F(x,d1,d2) – распределение Фишера (d1,d2>0 – числа степеней свободы).

· *gamma(x,s) – гамма-распределение (s>0 – параметр формы).

· *geom(k,p) – геометрическое распределение (0<р<1 – параметр, равный вероятности успеха единичного испытания).

· *hypergeom(k,a,b,n) – гипергеометрическое распределение (а,b,n – целые параметры).

· *lnоrm(х,m,o) – логарифмически нормальное распределение (m – натуральный логарифм математического ожидания, о>0 – натуральный логарифм среднеквадратичного отклонения).

· *logis(x,l,s) – логистическое распределение (l – математическое ожидание, s>0 – параметр масштаба).

· *nbinom(k,n,p) – отрицательное биномиальное распределение (n>0 – целый параметр, 0<р<1).

· *nоrm(х,m,o) – нормальное распределение (m– среднее значение, o>0 – среднеквадратичное отклонение).

· *pois(k,a) – распределение Пуассона (a>0 – параметр).

· *t(x,d) – распределение Стьюдента (d>0 – число степеней свободы).

· *unif(x,a,b) – равномерное распределение (а<b – границы интервала).

· *weibuli(x,s) – распределение Вейбулла (s>0 – параметр).

Статистические характеристики. Построение гистограмм.

В большинстве статистических расчетов Вы имеете дело либо со случайными данными, полученными в ходе какого-либо эксперимента (которые выводятся из файла или печатаются непосредственно в документе), либо с результатами генерации случайных чисел, рассмотренными в предыдущих разделах встроенными функциями, моделирующими то или иное явление методом Монте-Карло. Рассмотрим возможности Mathcad по оценке функций распределения и расчету числовых характеристик случайных данных.

Гистограммой называется график, аппроксимирующий по случайным данным плотность их распределения. При построении гистограммы область значений случайной величины (а,b) разбивается на некоторое количество bin сегментов, а затем подсчитывается процент попадания данных в каждый сегмент. Для построения гистограмм в Mathcad имеется несколько встроенных функций. Рассмотрим их, начиная с самой сложной по применению, чтобы лучше разобраться в возможностях каждой из функций.

Гистограмма с произвольными сегментами разбиения

· hist(intvis,x) – вектор частоты попадания данных в интервалы гистограммы;

o intvis – вектор, элементы которого задают сегменты построения гистограммы в порядке возрастания a<intvis_i<b;

o х – вектор случайных данных.

Если вектор intvis имеет bin элементов, то и результат hist имеет столько же элементов. Построение гистограммы иллюстрируется листингом и рис.7.

Листинг 1. Построение гистограммы:

Для анализа взято N=1000 данных с нормальным законом распределения, созданных генератором случайных чисел (третья строка листинга). Далее определяются границы интервала (upper, lower), содержащего внутри себя все случайные значения, и осуществляется его разбиение на количество (bin) одинаковых сегментов, начальные точки которых записываются в вектор int (предпоследняя строка листинга).

В векторе int можно задать произвольные границы сегментов разбиения так, чтобы они имели разную ширину.

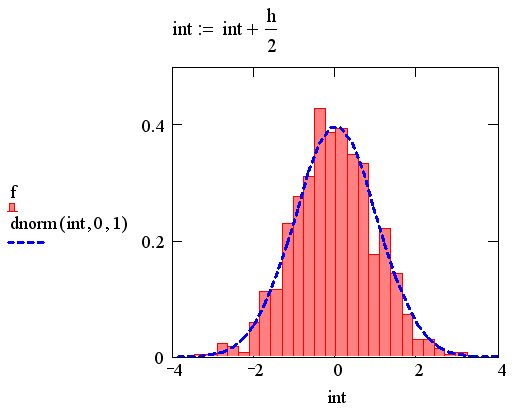
Рис. 7. Построение гистограммы (листинг 1)

Обратите внимание, что в последней строке листинга осуществлена нормировка значений гистограммы, с тем чтобы она правильно аппроксимировала плотность вероятности, также показанную на графике. Очень важно переопределение вектора int в самом верху рис. 7, которое необходимо для перехода от левой границы каждого элементарного сегмента к его центру.

Среднее значение и дисперсия

В Mathcad 11 имеется ряд встроенных функций для расчетов числовых статистических характеристик рядов случайных данных.

· mean(x) – выборочное среднее значение;

· median (х) – выборочная медиана (median) – значение аргумента, которое делит гистограмму плотности вероятностей на две равные части;

· var(x) – выборочная дисперсия (variance);

· stdev(x) – среднеквадратичное (или "стандартное") отклонение (standard deviation);

· max(x), mm (x) – максимальное и минимальное значения выборки;

· mode(x) – наиболее часто встречающееся значение выборки;

· var (x),stdev(x) – выборочная дисперсия и среднеквадратичное отклонение в другой нормировке;

o х – вектор (или матрица) с выборкой случайных данных.

Пример использования первых четырех функций приведен в листинге 14.10.

Расчет числовых характеристик случайного вектора:

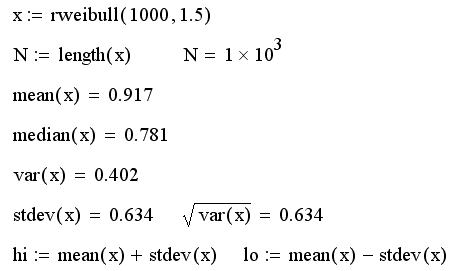
На рис. 8 приведена гистограмма выборки случайных чисел, распределенных согласно закону Вейбулла. Пунктирные вертикальные прямые, показанные на графике, рассчитаны в последней строке листинга и обозначают стандартное отклонение от среднего значения. Гистограмма получена с помощью листинга 14.8, рассмотренного в предыдущем разделе. Обратите внимание, что поскольку распределение Вейбулла, в отличие, например, от Гауссова, несимметричное, то медиана не совпадает со средним значением.

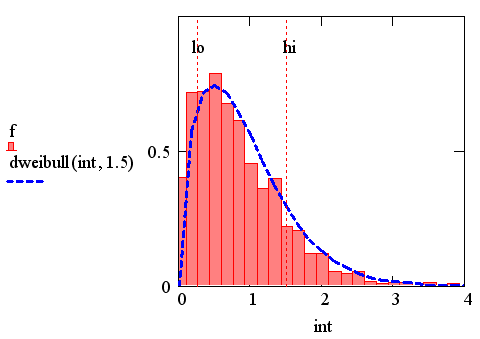
Рис. 8. Гистограмма распределения Вейбулла (листинг 14.10)

Определение статистических характеристик случайных величин приведено в листинге 14.11 на еще одном примере обработки выборки малого объема (по пяти данным). В том же листинге иллюстрируется применение еще двух функций, которые имеют смысл дисперсии и стандартного отклонения в несколько другой нормировке. Сравнивая различные выражения, Вы без труда освоите связь между встроенными функциями.

Генерация коррелированных случайных чисел. Ковариация и корреляция.

До сих пор мы рассматривали наиболее простой случай применения генераторов независимых случайных чисел. В методах Монте-Карло часто требуется создавать случайные числа с определенной корреляцией.

Приведем пример программы, создающей два вектора x1 и х2 одинакового размера и одним и тем же распределением, случайные элементы которых попарно коррелированы с коэффициентом корреляции R

Генерация попарно коррелированных случайных чисел:

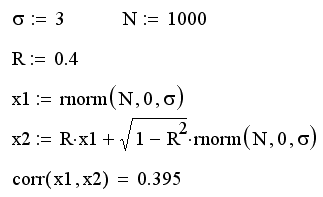
Результат действия программы для R=0.4 показан на рис. 9 (слева). Сравните полученную выборку с правым графиком, полученным для высокой корреляции (R=0.9) и с рис. 9для независимых данных, т. е. R=0.

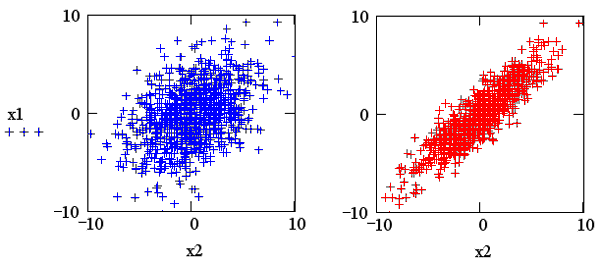
Рис. 9 Псевдослучайные числа с корреляцией R=0.4 (листинг 14.12) и R=0.9

Ковариация и корреляция

Функции, устанавливающие связь между парами двух случайных векторов, называются ковариацией и корреляцией (или, по-другому, коэффициентом корреляции). Они различаются нормировкой, как следует из их определения.

· согг(х) – коэффициент корреляции двух выборок;

· cvar(x) – ковариация двух выборок;

o x1, х2 – векторы (или матрицы) одинакового размера с выборками случайных данных.

Коэффициенты асимметрии и эксцесса. Другие статистические характеристики.

Коэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящий через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическим ожиданием, например нормальным, все нечетные моменты, в том числе и третий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю.

Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной – коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса больше нуля, то распределение имеет более острую вершину, чем распределение Гаусса, если меньше нуля, то более плоскую.

Для расчета коэффициентов асимметрии и эксцесса в Mathcad имеются две встроенные функции.

· kurt(x) – коэффициент эксцесса (kurtosis) выборки случайных данных х;

· skew(x) – коэффициент асимметрии (skewness) выборки случайных данных x.

Расчет выборочных коэффициентов асимметрии и экспресса:

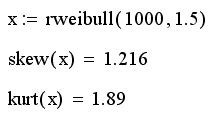
Другие статистические характеристики

В предыдущих разделах были рассмотрены встроенные функции, рассчитывающие наиболее часто используемые статистические характеристики выборок случайных данных. Иногда в статистике встречаются и иные функции, например, помимо арифметического среднего, применяются другие средние значения.

· gmean(x) – геометрическое среднее выборки случайных чисел;

· hmean(x) – гармоническое среднее выборки случайных чисел.

Случайные процессы

Встроенные функции для генерации случайных чисел создают выборку из случайных данных АХ. Часто требуется создать непрерывную или дискретную случайную функцию A(t) одной или нескольких переменных (случайный процесс или случайное поле), значения которой будут упорядочены относительно своих переменных. Создать псевдослучайный процесс можно способом, представленным в листинге 14 19.

Генерация псевдослучайного процесса:

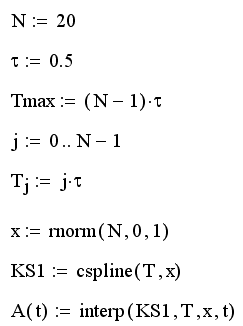
В первой строке определено количество N независимых случайных чисел, которые будут впоследствии сгенерированы, и радиус временной корреляции т. В следующих трех строках определяются моменты времени тэ, которым будут отвечать случайные значения A(t.,). Создание нормального случайного процесса сводится к генерации обычным способом вектора независимых случайных чисел х и построению интерполяционной зависимости в промежутках между ними.

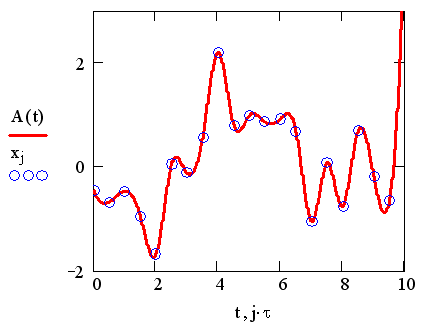
Рис. 10Псевдослучайный процесс (листинг 14.19)