Введение в статистический анализ данных

· Базовые понятия статистического анализа данных

· Подходы к статистическому анализу данных

· Этапы статистической обработки

– Предварительный статистический анализ данных

– Оценка закона распределения. Непараметрический подход

– Оценка закона распределения. Параметрический подход

– Восстановление пропущенных значений и анализ выбросов

– Унификация признакового описания

Базовые понятия статистического анализа данных

Этапы работ, предшествующие обработке экспериментальных данных

Всех специалистов, профессионально занимающихся обработкой статистических данных, условно можно разделить на три категории: 1) приверженцы классической математической статистики (объектами их исследований обычно являются некоторые разделы биологии или физики); 2) представители школы обработки экспериментальных данных в рамках идеологии исследования операций (предметом их разработок чаще всего бывают результаты активных экспериментов над сложной технической системой); 3) специалисты по прикладной статистике и анализу данных, ориентированные на исследование естественных и социальных систем в таких, например, областях, как геология, медицина, экономика и социология. Характер данных и методологическое видение проблемного материала во всех трёх случаях столь различны, что в действительности эти три течения статистических исследований следовало бы признать самостоятельными. В настоящей лекции за основу принята концепция по отношению к прикладной статистике и анализу данных, окончательно сформировавшаяся к концу 80-х годов. Наиболее полно эта область прикладной математики изложена в трёхтомном справочном издании по прикладной статистике под редакцией С.А.Айвазяна. В текстах лекций использована концепция стиля подачи материала упомянутого выше справочника.

Прикладная статистика

Целесообразность введения термина прикладная статистика наряду с привычным понятием математическая статистика объясняется тем, что для внедрения метода статистической обработки необходимо дополнительно провести сложную и наукоемкую работу. Условно разобьем её на ряд этапов: 1) адекватно «приложить» исходные модельные допущения к реальной задаче; 2) представить имеющуюся исходную информации (физические сигналы, геологические срезы и др.) в стандартной форме; 3) разработать вычислительный алгоритм и его программное обеспечение; 4) организовать удобный режим общения с ЭВМ в процессе решения задачи. Весь комплекс выше перечисленных действий и составляет содержание прикладной статистики

Исходя из выше сказанного, дадим определение, введенное в 1983г. С.А. Айвазяном [1, стр 19]. Прикладная статистика – это самостоятельная научная дисциплина, разрабатывающая и систематизирующая понятия, приемы, математические методы и модели предназначенные для организации сбора, стандартной записи, обработки статистических данных с целью их удобного представления (в том числе и на ЭВМ), интерпретации и получения научных и практических выводов.

Заметим, что некоторые специалисты, в частности, французские, вместо введенного термина «прикладная статистика» используют понятие «анализ данных», трактуя его в расширительном смысле.

Идеи и методологические принципы многомерного статистического анализа данных

Эффект существенной многомерности. Статистический анализ должен опираться одновременно на совокупность взаимосвязанных свойств объектов.

Возможность лаконичного объяснения природы анализируемых многомерных структур. На нем построены такие важнейшие разделы математического аппарата классификации и снижения размерности, как метод главных компонент и факторный анализ, многомерное шкалирование, целенаправленное проецирование в разведочном анализе данных и др.

Максимальное использование «обучения» в настройке математических моделей многомерного статистического анализа данных.

Оптимизационная формулировка задач многомерного статистического анализа данных.

Цели эксперимента в науке и промышленности

Экспериментальные методы широко используются как в науке, так и в промышленности, однако нередко с весьма различными целями. Обычно основная цель научного исследования состоит в том, чтобы показать статистическую значимость эффекта воздействия определенного фактора на изучаемую зависимую переменную. В условиях промышленного эксперимента основная цель обычно заключается в извлечении максимального количества объективной информации о влиянии изучаемых факторов на производственный процесс с помощью наименьшего числа дорогостоящих наблюдений. Если в научных приложениях методы дисперсионного анализа используются для выяснения реальной природы взаимодействий, проявляющейся во взаимодействии факторов высших порядков, то в промышленности учет эффектов взаимодействия факторов часто считается излишним в ходе выявления существенно влияющих факторов.

Указанное отличие приводит к существенному различию методов, применяемых в науке и промышленности. Если просмотреть классические учебники по дисперсионному анализу, то обнаружится, что в них, в основном, обсуждаются планы с количеством факторов не более пяти (планы же с более чем шестью факторами обычно оказываются бесполезными). Основное внимание в данных рассуждениях сосредоточено на выборе общезначимых и устойчивых критериев значимости. Однако если обратиться к стандартным учебникам по экспериментам в промышленности, то окажется, что в них обсуждаются, в основном, многофакторные планы (например, с 16-ю или 32-мя факторами), в которых нельзя оценить эффекты взаимодействия, и основное внимание сосредоточивается на том получении несмещенных оценок главных эффектов (или, реже, взаимодействий второго порядка) с использованием наименьшего числа наблюдений.

Подходы к статистическому анализу данных

Возможные подходы к статистическому анализу данных

Развитие теории и практики статистической обработки данных шло в двух параллельных направлениях. Первое включает методы математической статистики, предусматривающие возможность классической вероятностной интерпретации анализируемых данных и полученных статистических выводов (вероятностный подход). Второе направление содержит статистические методы, которые априори не опираются на вероятностную природу обрабатываемых данных, т.е. остаются за рамками научной дисциплины «математическая статистика» (логико-алгебраический подход). Ко второму подходу исследователь вынужден обращаться лишь тогда, когда условия сбора исходных данных не укладываются в рамки статистического ансамбля, т.е. в ситуации, когда не имеется практической или хотя бы принципиально мысленно представимой возможности многократного тождественного воспроизведения основного комплекса условий, при которых производились измерения анализируемых данных.

Типы реальных ситуаций с позиции выполнения требований статистического ансамбля

Выделяют три типа реальных ситуаций: с высокой работоспособностью вероятностно-статистических методов; с допустимостью вероятностно-статистических приложений (при этом нарушатся требования сохранения неизменными условия эксперимента); с недопустимостью вероятностно-статистических приложений (в этом случае идея многократного повторения одного и того же эксперимента в неизменных условиях является бессодержательной).

Сравнение подходов к статистическому анализу данных

Основные отличительные особенности подходов на примере задачи классификации представим схематично в таблице 2.1.

Таблица 1– Отличительные особенности подходов

Составляющие	Первое направление	Второе направление
Цели исследования	Выделение классов, как инвариантов в потоке выборочных объектов	Выяснение распределения данных в системе
Объекты и признаки.	Независимы	Зависимость предполагается, ее нужно обнаружить
Выделяемые классы	Характеризуются эталоном и не пересекаются	Четко не выделяются, т.е. пересекаются
Аппарат исследования	Вероятностный - преобразование пространства признаков (даже в одномерную ось)	Логико-комбинаторный

Первое направление развития анализа данных, ориентированное на технические области знания, отстаивает идею простоты используемых моделей. В рамках этого направления неудовлетворительные результаты объясняют отсутствием информативных признаков.

Второе направление развития анализа данных ориентировано на социально-экономическую и социологическую информацию. При ее обработке появилось много новых идей, в частности, идея поэтапной группировки и коллектива решающих правил. Разработаны методы многомерного шкалирования, экспертных оценок.

В отличие от первого примера во втором примере невозможно: интерпретировать исходные данные в качестве случайной выборки генеральной совокупности (в связи с неприятием главной идеи понятия статистического ансамбля: идея многократного повторения одного и того же эксперимента в неизменных условиях теряет смысл); использовать вероятностную модель для построения и выбора наилучших методов статистической обработки; дать вероятностную интерпретацию выводам, основанным на статистическом анализе исходных данных.

Но в обоих случаях выбор наилучшего из всех возможных методов обработки данных производится в соответствии с некоторыми функционалами качества метода. Способ обоснования выбора этого функционала, а также его интерпретация различны. В первом случае выбор основан на допущении о вероятностной природе исходных данных и интерпретация тоже. Во втором случае исследователь не пользуется априорными сведениями о вероятностной природе исходных данных и при обосновании выбора оптимального критерия качества опирается на соображения содержательного (физического) плана - как именно и для чего получены данные. Когда критерий выбран, в обоих случаях используются методы решения экстремальных задач. На этапе осмысления и интерпретации каждый из подходов имеет свою специфику.

При выборе типа модели следует понимать, что всякая модель является упрощенным (математическим) представлением изучаемой действительности. Мера адекватности модели и действительности является решающим фактором работоспособности используемых затем методов обработки. А так как ни одна модель не может идеально соответствовать реальной ситуации, то желательна многократная обработка исходных данных для разных вариантов модели.

Этапы статистической обработки

Основные этапы статистической обработки экспериментальных данных

Опишем общую логическую схему статистического анализа данных в виде семи этапов, перечислив их в хронологическом порядке (хотя они могут реализовываться в режиме итерационного взаимодействия).

Этап 1 Исходный (предварительный) анализ исследуемой системы. На этом этапе определяются: основные цели исследования на неформализованном, содержательном уровне; совокупность единиц (объектов), представляющая предмет статистического исследования; набор параметров-признаков для описания обследуемых объектов; степень формализации соответствующих записей при сборе данных; время и трудозатраты, объем работ; выделение ситуаций, требующих предварительной проверки перед составлением детального плана исследований; формализованная постановка задачи; в каком виде осуществляется сбор первичной информации и введение в ЭВМ.

Если обработка проводится с помощью существующего пакета статистической обработки, то трудоемкость этого этапа бывает сравнима с суммарной трудоемкостью остальных этапов.

Этап 2 Составление плана сбора исходной информации. При составлении детального плана сбора первичной информации необходимо учитывать как и для чего данные анализируются, т.е. учитывать полную схему анализа. Этот этап называют «организационно-методической подготовкой», так как на нем планируется: какой должна быть выборка – случайной, пропорциональной, расслоенной (если используется аппарат общей теории выборочных обследований); объем и продолжительность исследования; схема проведения активного эксперимента (в случае, если он возможен) с привлечением методов планирования эксперимента и регрессионного анализа для определения некоторых входных переменных.

Этап 3 Сбор исходных данных, их подготовка и введение в ЭВМ. Сбор исходных данных и введение их в ЭВМ, а также внесение в ЭВМ полного и краткого определения используемых терминов. Существует два вида представления исходных данных: матрица «объект-признак»: со значениями k-го признака, характеризующего i-й объект в момент t (числа, текст): , , , ; и матрица «объект-объект» - характеристик попарной близости i-го и j-го объектов (при этом m=N) или признаков (при этом m=p) в момент t. Второй вид представления часто используется в социологии, где данные собираются с помощью специальных опросников, анкет. Примером характеристики попарной близости признаков может служить ковариационная матрица.

Этап 4 Первичная статистическая обработка данных. При первичной статистической обработке данных обычно решаются следующие задачи: отображение вербальных переменных в номинальную (с предписанным числом градаций) или ординальную (порядковую) шкалу; статистическое описание исходных совокупностей с определением пределов варьирования переменных; анализ резко выделяющихся переменных; восстановление пропущенных значений наблюдений; проверка статистической независимости последовательности наблюдений, составляющих массив исходных данных; унификация типов переменных, когда с помощью различных приёмов добиваются унифицированной записи всех переменных; экспериментальный анализ закона распределения исследуемой генеральной совокупности и параметризация сведений о природе изучаемых распределений (эту разновидность первичной статистической обработки называют иногда процессом составления сводки и группировки); вычислительная реализация учета сложности задачи и возможностей ЭВМ; формулировка задачи на входном языке пакета статистической обработки.

Этап 5 Выбор основных методов и алгоритмов статистической обработки данных, составление детального плана вычислительного анализа материала. Составление детального плана вычислительного анализа. Определяются основные группы, для которых будет проводиться дальнейший анализ. Пополняется и уточняется тезаурус содержательных понятий. Описывается блок-схема анализа с указанием привлекаемых методов. Формируется оптимизационный критерий, по которому выбирается один из альтернативных методов.

Этап 6 Реализация плана вычислительного анализа исходных данных (непосредственная эксплуатация ЭВМ

Исследователь на этом этапе осуществляет управление вычислительным процессом, формирует задачу обработки и описания данных на входном языке пакета. Учитываются размерность задачи, алгоритмическая сложность вычислительного процесса, возможности ЭВМ, и особенности данных (обусловленность операций, надежность используемых оценок параметров).

Этап 7 Подведение итогов. Строится формальный отчет о проведенном исследовании. Интерпретируются результаты применения статистических процедур (оценки параметров, проверки гипотез, отображения в пространство меньшей размерности, классификации). При интерпретации могут использоваться методы имитационного моделирования.

Если исследование проводится в рамках первого подхода (см. п.1.2), то выводы формируются в терминах оценок неизвестных параметров, или в виде отчета о справедливости гипотез с указанием количественной степени достоверности. В случае второго подхода вероятностная интерпретация не делается.

Работа завершается содержательной формулировкой новых задач, вытекающих из проведенного исследования.

Основная цель разведочного анализа данных

Этап разведочного анализа данных (РАД) зачастую игнорируется или реализуется поверхностно в ходе прикладных статистических исследований. Одна из главных причин – отсутствие необходимой научно-методологической литературы. Большое внимание этим вопросам уделено в третьем томе справочника по прикладной статистике Айвазяна С.А. и др. Основная цель РАД – построить некоторую статистическую модель в виде эмпирического описания структуры данных, которую необходимо будет потом в ходе статистического исследования верифицировать. Основная задача РАД – переход к компактному описанию данных при возможно более полном сохранении существенных аспектов информации, содержащихся в данных.

Методы разведочного анализа данных

Методы разведочного (предмодельного) статистического анализа данных, направлены на «прощупывание» вероятностной и геометрической природы обрабатываемых данных и предназначены для формирования адекватных реальности рабочих исходных допущений, на которых строится дальнейшее исследование. РАД является необходимым и естественным моментом первичной статистической обработки и применяется, когда отсутствует априорная информация о статистическом или причинном механизме порождения имеющихся у исследователя данных.

Важнейшим элементом РАД является широкое использование визуального представления многомерных данных. Его возможности возросли благодаря появлению динамических форм визуального представления. Для этого многомерные данные отображаются в пространство низкой размерности с сохранением существенных структурных особенностей. При этом структура данных может оказаться такой сложной, что небольшого числа проекций недостаточно для их представления. Тогда структуру описывают за счет агрегирования информации, содержащейся в большом числе низкоразмерных проекций.

К РАД относятся методы, дающие наглядное представление о структуре многомерных данных в пространствах малой размерности. В случае, если размерность пространства, куда отображаются данные, меньше или равно трем, то эти методы относятся к собственно разведочному анализу, когда по некоторому критерию при помощи вычислительной процедуры оптимизации ищут отображения, дающие наиболее выразительные проекции, а окончательное решение принимается визуально путем анализа (в одномерном случае – это гистограмма, на плоскости – диаграмма рассеивания).

К РАД относятся также методы, связанные с линейным проецированием, упрощением описания с помощью компонентного анализа и многомерного шкалирования, кластер-анализа, анализа соответствий (для неколичественных переменных).

Модели структуры многомерных данных в разведочном анализе данных

Пусть данные заданы в виде матрицы данных. Объекты можно представить в виде точек в многомерном (р-мерном) пространстве. Для описания структуры этого множества точек в РАД используется одна из следующих статистических моделей:

1- модель облака точек примерно эллипсоидальной конфигурации;

2- кластерная модель, т.е. совокупность нескольких «облаков» точек, достаточно далеко отстающих друг от друга;

3- модель «засорения» (компактное облако точек и при этом присутствуют дальние выбросы);

4- эмпирический образ данных в виде покрытия выборочных точек многомерного признакового пространства сетью гиперпараллелепипедов с оцененной плотностью распределения (многомерный аналог гистограммы);

5- модель носителя точек как многообразия (линейного или нелинейного) более низкой размерности, чем исходное: типичным примером является выборка из вырожденного распределения; в рамках этой модели можно рассматривать и регрессионную модель, когда соответствующие многообразие допускает функциональное представление , где Х₁₁- прогнозируемые, -предсказывающие признаки, - функция регрессии,- ошибка.

6- дискриминантная модель, когда точки разделены на несколько групп и дана информация о их принадлежности к той или иной группе.

.

Предварительный статистический анализ данных

Любое экспериментальное исследование содержит этапы постановки задачи, планирования и проведения эксперимента, а также анализа и интерпретация результатов. Главной трудностью на этапе постановки задачи является переход с языка специальности на язык планирования эксперимента, на язык математики.

Содержательная постановка задач статистического описания и прогноза является переходной формулировкой, позволяющей перейти к математической, на основании выявленной цели исследования. Математическая постановка задач статистического описания и прогноза предполагает то, что формулировка задачи будет сделана в терминах, используемых в конкретной формальной дедуктивной системе.

Математическая постановка задач статистического описания предназначена для описания структуры множества выборочных точек и для формирования адекватных реальности рабочих исходных допущений, на которых строится дальнейшее исследование. В вероятностно-статистическом подходе математическая постановка задач статистического описания может состоять в оценке закона распределения. В логико-комбинаторном подходе, или в РАД используется одна из первых четырех статистических моделей: модель облака точек, кластерная модель, модель «засорения» и эмпирический образ данных

В общем виде задачу классификации исследуемой совокупности N объектов O={O_i}, , где для каждого объекта замерены значения p параметров, т.е. каждый объект O_i описан вектором X_i = (x_i¹,…,x_i^r), можно сформулировать как задачу поиска такого разбиения S заданной совокупности на непересекающиеся классы S₁,….,S_k: ,=Æ, i¹j, при котором функционал качества Q(S) достигает экстремального значения на множестве A допустимых правил классификации. В качестве Q(S) используют критерии, минимизирующие межгрупповое сходство и одновременно максимизирующее внутригрупповое сходство. Состав множества A зависит от предварительной (априорной) выборочной информации об этих классах. Итак, задача классификации формально сводится к нахождению разбиения S*: для S Î A. Заметим, что при этом число k может быть и неизвестно. При любых трактовках кластеров и для различных методов классификаций неизбежно возникает проблема измерения близости объектов. С этой проблемой связаны следующие трудности: неоднозначность выбора способа нормировки и определения расстояния между объектами.

Содержательная и математическая постановка задачи статистического прогноза

Построение математической модели, например. Технологического процесса в зависимости от поставленной задачи может преследовать следующие цели: минимизировать расход материала на единицу выпускаемой продукции при сохранении качества, произвести замену дорогостоящих материалов на более дешевые или дефицитных на распространение; сократить время обработки в целом или на отдельных операциях, перевести отдельные режимы в некритические зоны, снизить трудовые затраты на единицу продукции и т.п.; улучшить частные показатели и общее количество готовой продукции, повысить однородность продукции, улучшить показатели надежности и т.п.; увеличить надежность и быстродействие управления, увеличить эффективность контроля качества, создать условия для автоматизации процесса управления и т.п. Прежде всего, необходимо выбрать зависимую переменную Y, которую обычно называют целевой функцией или параметром оптимизации, за который принимают один из показателей качества продукции либо по каждой технологической операции отдельно, либо по всему технологическому процессу сразу. Параметр оптимизации должен соответствовать следующим требованиям: параметр должен измеряться при любом изменении (комбинации) режимов технологического процесса; параметр должен быть статистически эффективным, то есть измеряться с наибольшей точностью; параметр должен быть информационным, то есть всесторонне характеризовать технологический процесс (операцию); параметр должен иметь физический смысл, то есть должна быть возможность достижения полезных результатов при соответствующих условиях процесса; параметр должен быть однозначным, т.е. должно минимизироваться или максимизироваться только одно свойство изделия.

Для достоверного отображения объективно существующих процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого.

Сформулируем математическую постановку задачи статистического прогноза на примере задачи регрессионного анализа в п.3.

Схема взаимодействия переменных при статистическом исследовании зависимостей

Основная цель статистического исследования зависимостей (СИЗ) состоит в том, чтобы на основании частных результатов статистического наблюдения за показателями двух или трех различных явлений, происходящих с исследуемым объектом, выявить и описать существующие взаимосвязи. В случае численного выражения такие показатели называют переменными.

Рамки применения аппарата СИЗ определяются двумя условиями: - стохастичность интересующей нас взаимосвязи между переменными (т.е. реализация явления или события А одной переменной может повлечь за собой событие В другой переменной с вероятностью р); - взаимосвязь между переменными выявляется на основе статистических наблюдений по выборкам из соответствующих генеральных совокупностей событий.

Опишем функционирование изучаемого реального объекта набором переменных, среди которых выделим: x⁽¹⁾,..., x^(p) - «входные» переменные, описывающие условия или причинные компоненты функционирования (поддаются контролю или частичному управлению); для них используются такие термины как факторы-аргументы, факторы-причины, экзогенные, предикторные (предсказательные), объясняющие; y⁽¹⁾,..., y^(m) - «выходные», характеризующие поведение объекта или результат (эффективность) функционирования; обычно их называют отклики, эндогенные, результирующие, объясняемые, факторы-следствия, целевые факторы; e⁽¹⁾,..., e^(m) - латентные (скрытые, не поддающиеся непосредственному измерению) случайные «остаточные» компоненты, отражающие влияние на y⁽¹⁾,..., y^(m) неучтенных «на входе» факторов, а также случайные ошибки в измерении анализируемых показателей; остатки.

Используя введенный набор переменных, задача СИЗ может быть сформулирована следующим образом: по результатам N измерений

исследуемых переменных на N объектах построить такую (векторно-значимую) функцию

,

которая позволила бы наилучшим образом восстановить значения переменных по заданным значениям объясняющих переменных .

Математический инструментарий СИЗ

Методы СИЗ составляют содержание отдельных частей многомерного статистического анализа, которые можно определить как раздел математической статистики, посвященный построению оптимальных планов сбора, систематизации и обработки многомерных статистических данных, нацеленных на выявление характера и структуры взаимосвязей между компонентами (X,Y) и предназначенных для получения практических и научных выводов. Среди p+m компонент могут быть: количественные, порядковые (ординальные), классификационные (номинальные).

Методы СИЗ формировались с учетом специфики моделей, обусловленных природой изучаемых переменных. Схематично всю совокупность методов приведем в таблице 6.1.

Таблица 2 - Математический инструментарий СИЗ

Природа результирующих показателейY	Природа объясняющих переменных X	Названия обслуживающих разделов многомерного статистического анализа
Количественная	Количественная	Регрессионный и корреляционный анализ
Количественная	Одна количественная переменная, интерпретируемая, как время	Анализ временных рядов
Количественная	Неколичественная (ординальные или номинальные переменные)	Дисперсионный анализ
Количественная	Смешанная (количественные и неколичественные переменные)	Ковариационный анализ, модели типологической регрессии
Неколичественная (порядковые переменные)	Неколичественная (ординальные или номинальные переменные)	Анализ ранговых корреляций и таблиц сопряженности
Неколичественная (номинальные переменные)	Количественная	Дискриминантный анализ, кластер-анализ, расщепление смесей распределения
Смешанная (количественные и неколичественные переменные)	Смешанная (количественные и неколичественные переменные)	Аппарат построения логических решающих функций и эмпирического образа данных

Краткая характеристика математического инструментария

Корреляционный анализ оценивает степень тесноты статистической взаимосвязи и обосновывает целесообразность регрессионного анализа. Регрессионный анализ позволяет получить прогноз количественных значений результирующей переменной по значениям входных. Анализ временных рядов занимается исследованием поведения результирующих переменных во времени. Дисперсионный анализ выявляет наличие взаимосвязи между качественными показателями и результирующей переменной.

Оценка закона распределения. Непараметрический подход

Разновидности первичной статистической обработки

При первичной статистической обработке данных обычно решаются следующие задачи: отображение вербальных переменных в номинальную (с предписанным числом градаций) или ординальную (порядковую) шкалу; статистическое описание исходных совокупностей с определением пределов варьирования переменных; анализ резко выделяющихся переменных; восстановление пропущенных значений наблюдений; проверка статистической независимости последовательности наблюдений, составляющих массив исходных данных; унификация типов переменных, когда с помощью различных приёмов добиваются унифицированной записи всех переменных; экспериментальный анализ закона распределения исследуемой генеральной совокупности и параметризация сведений о природе изучаемых распределений (эту разновидность первичной статистической обработки называют иногда процессом составления сводки и группировки); вычислительная реализация учета сложности задачи и возможностей ЭВМ; формулировка задачи на входном языке пакета статистической обработки.

Параметрическое и непараметрическое оценивание закона распределения

Первичные данные, полученные при наблюдении, обычно трудно обозримы. Для того, чтобы начать анализ, в них надо внести некоторый порядок и придать им удобный для исследователя вид. В частности, для начала желательно получить представление об одномерных распределениях случайных величин, входящих в данные.

Существуют два типа задач аппроксимации распределений. Если вид функции распределения известен, но не известны ее параметры, тогда задача сводится к параметрическому оцениванию. Бывают ситуации, когда конкретный вид функции распределения неизвестен и о виде распределения можно сделать лишь самые общие предположения. При таких условиях аппроксимацию неизвестной функции распределения на основе выборки называют непараметрической.

Равноинтервальная гистограмма и полигон частот

Классическими методами статистической аппроксимации функции плотности являются гистограмма (равноинтервальная и равнонаполненная) и полигон частот.

Выборочная функция плотности распределения или гистограмма (равноинтервальная) строится следующим образом. Делим промежуток [a,b], на котором сосредоточены данные выборки на S интервалов , равной длины h=(b-a)/S. Подсчитываем число наблюдений , попавших в интервал , соответственно. Полагаем Полигон частот получают путем сглаживания гистограммы

, ,

где - середина промежутка , -правый конец промежутка .

Очевидно, что .

Равнонаполненная гистограмма и полигон частот

Выборочная функция плотности распределения или гистограмма (равнонаполненная) строится исходя из предположения, что вся площадь под графиком оценки функции разбивается на k равных частей. Тогда площадь каждой части равна , . Для конкретной выборки рассчитываются длины интервалов , а затем по формуле , определяется . На основании полученных значений длины и высоты каждого прямоугольника гистограммы получаем оценку .

Метод прямоугольных вкладов

Для малых выборок (N<30) гистограмма и полигон частот оказываются обычно искаженными за счет тех или иных случайных локальных отклонений, связанных с отсутствием необходимого числа объектов. Одним из способов частично ликвидировать этот пробел явилась «ядерная» аппроксимация, которая путем «размазывания» имеющихся точек заполняет на гистограмме «впадины» и срезает «пики». Отметим, что «ядерное» сглаживание учитывает особенность функции плотности распределения и потому из всех методов сглаживания является наиболее корректным.

Ядерная аппроксимация закона распределения. Оценка плотности распределения для большинства методов «ядерного» типа обобщенно может быть выражена линейной суммой двух компонент: априорной и эмпирической:

,

где - априорная компонента; - составляющая эмпирической компоненты, связанная с i- ой реализацией выборки (заметим, что играет роль параметра); - вес априорной компоненты.

Различным методам исследования соответствуют разные значения и разные виды функции . Широко известны оценки «ядерного» типа для f(x) при значении .

В методе прямоугольных вкладов (МПВ)

, ,

где [a,b] -интервал изменения случайной величины x; d - ширина функции вклада.

В качестве d может быть взято, например: , где.

Алгоритм ядерной аппроксимации функции плотности распределения имеет следующий вид.

Этап 1. Задается множество точек : ;

Этап 2. Полученное множество точек упорядочивается по возрастанию: ;

Этап 3. Определяется «ядерная» аппроксимация функции плотности распределения :

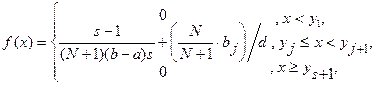
где - количество точек исходной выборки, попавших в интервал , а () –некоторое подмножество точек из множества .

Оценка закона распределения. Параметрический подход

Нормальная вероятностная бумага

Пусть даны N наблюдений x₁,…,x_N, извлеченные из генеральной совокупности с функцией распределения F(t). Пусть x⁽¹⁾,…,x^(N)- упорядоченный по возрастанию ряд наблюдений. Тогда за оценку F(t) принимают , где ;

В тех случаях, когда требуется проверить гипотезу о том, что случайная величина имеет функцию распределения G(t), принадлежащую семейству вида F((t-m)/s), где F(.) известная непрерывная функция распределения, при построении оценки часто используют специальную шкалу, откладывая по оси ординат вместо величину , где - функция, обратная к F. В этом случае в координатах (t,v) график G(t) превращается в прямую линию, по положению которой можно легко оценить параметры m и s. Заметим, что наибольшее распространение на практике получила нормальная вероятностная бумага, для которой , где Ф(.)- стандартная функция нормального распределения.

Опишем алгоритм оценки с помощью вероятностной бумаги параметров центраи разброса . Работа осуществляется в несколько этапов.

Этап 1. Строится вероятностная бумага. Для этого внизу окна графика на оси абсцисс (см.рис.) откладывается интервал . Масштаб подбирается так, чтобы интервал занял ширину окна, за исключением левого отступа 7-8 см. Ось ординат проводится с отступом от левого края 4-5 см. При этом пунктиром отделяется шкала величины V=Ф^-1 , которая равномерно изменяется от -3 до 3. Таким образом, точка V=-3.0 будет находиться на оси абсцисс, а точка V=3.0 будет находиться в верхнем левом углу. Слева от пунктирной оси делаются отметки шкалы V, а между осью V и отметки вероятности р: 0.01;0.05;0.1;0.25;0.5;0.75;0.9;0.95;0.99.

Шкала вероятностей является неравномерной. Засечка вероятности осуществляется следующим образом. Берется вероятность р=0.01. По таблицам нормальной функции распределения находится значение . Напротив полученного значения V ставится засечка 0.01 на шкале вероятностей. Далее берется вероятность р=0.05 и т.д.

Этап 2. Исходная выборка значений упорядочивается по возрастанию. В результате получается последовательность x⁽¹⁾ ,…, x^(N).

Этап 3. Для каждого значения x⁽ⁱ⁾ , на плоскости отмечается точка (x⁽ⁱ⁾ , i/N ). Для того, чтобы определить расположение этой точки, находится значение V_i=Ф^-1( i / N ) , которое откладывается по оси V .

Рисунок 1. Оценка параметров нормального распределения на нормальной вероятностной бумаге

Этап 4. Если точки (х⁽ⁱ⁾ ,i/N) в какой-то мере ложатся вдоль некоторой прямой, то можно грубо считать генеральную совокупность, из которой извлечена данная выборка, нормальной. В противном случае надо подыскать преобразование переменной, например, логарифмирование, извлечение корня и т.п., в результате которого выборка бы соответствовала нормальному распределению.

Этап 5. В случае принятия гипотезы о нормальности распределения осуществляется оценка параметров распределения. В качестве оценки центра берется медиана выборки, которая соответствует вероятности р=0.5. Оценка стандартного отклонения , где - оценка 0.84 квантиля распределения, полученного при V=1.

Параметрическое оценивание

Построение гистограммы, полигона частот и ядерной аппроксимации основано на локальной интерполяции. Другой подход к аппроксимации заключается в интерполировании закона распределения на всем интервале [a,b]. К методам этого типа относится аппроксимация с помощью системы кривых Пирсона. Систему кривых Пирсона получают путем выравнивания дискретного гипергеометрического распределения непрерывной кривой. При этом для выбора подходящей кривой используют четыре первых момента выборочного распределения. Отметим, что практического распространения данный способ аппроксимации распределения не получил в связи с неустойчивостью моментов первого порядка и невозможностью интерпретации механизма генерации выборки полученного типа распределения.

Критерием согласия

Более популярными среди интегральных методов аппроксимации оказались параметрические методы оценки распределения путем проверки на согласие данного эмпирического распределения с конкретным теоретическим распределением, например, нормальным, экспоненциальным и т.д. В реальной ситуации тип распределения часто бывает известен. Кроме того, просмотрев гистограмму или полигон частот, пользователь для себя уже принимает общепризнанную гипотезу H₀ о типе распределения (или наоборот, отвергает ее из-за сильного засорения выборки, смешения в ней двух или более подвыборок из разных генеральных совокупностей). Математический аппарат в виде критерия согласия используется здесь с целью подтверждения и оформления решения пользователя.

Воспользуемся - критерием согласия. Процедура проверки гипотезы H₀ в данном случае будет состоять из следующих этапов.

Этап 1. Область изменения выборки [a,b] делим на S равных интервалов, как при построении гистограммы. Если в каком-то интервале частота слишком мала (меньше 5), то этот интервал объединяется с соседним интервалом. Таким образом количество интервалов может уменьшиться и стать равным S'.

Этап 2. По выборке вычисляют оценки параметров теоретического распределения (тем самым теоретическое распределение будет полностью определено). Теперь по теоретическому распределению вычислим вероятности того, что случайная величина Х принимает значение из s-го интервала, при этом . Затем найдем теоретические частоты .

Этап 3. Гипотеза Н₀ верна, если теоретические и эмпирические частоты n_s и m_s достаточно мало отличаются друг от друга. Для проверки гипотезы Н₀ используем следующую статистику:

Этап 4. Случайная величина имеет распределение с числом степеней свободы v=S'-r-1, где S' - количество интервалов, r -количество параметров теоретического распределения, оценки которого вычислялись по выборке. Чем больше . тем хуже согласованы теоретическое и эмпирическое распределения. При достаточно большом значении нужно отвергнуть гипотезу Н₀. Поэтому используем только правостороннюю критическую область. Р - значением является площадь области под функцией плотности распределения справа от точки (см. таблицу процентилей распределения ). Если P < , то мы отвергаем Н₀ и принимаем гипотезу Н₁: теоретическое и эмпирическое распределения не согласованы. Здесь - это уровень значимости, который обычно принимается равным 0.05.

Восстановление пропущенных значений и анализ выбросов

Восстановление пропущенных значений

Непараметрический подход к оценке пропусков в матрице данных. Наряду с подходом, требующим аналитического задания закона распределения, существует и другой, основанный на использовании расстояния между параметрами объектов (в некоторой метрике), определяемого по значениям признаков, измеренных у обоих объектов. Постулируется, что, если два объекта близки в пространстве измеренных признаков, то они должны быть близки и в пространстве по неизмеренным признакам. Метрика и пороговое значение расстояния, определяющие близость объектов, вводятся в зависимости от условий задачи (шкалы, количества признаков).

Алгоритм ZET

Рассмотрим схематично конкретизацию этого подхода в известном алгоритме ZET. Пусть у объекта X_i требуется оценить значение пропущенного признака x^(j) , т.е. оценить в матрице X. Для этого в X выделяется подмножество объектов, у которых измерено значение j-го признака. В этом подпространстве выделяется однородная группа объектов наиболее близких к X_i в подпространстве признаков, полученном из исходного пространства исключением j-го признака. Неизмеренное значение заменяется средним по выделенной группе объектов. Для оценки качества заполнения пропусков ввести формализованный критерий трудно. Приближенно его оценивают например так: из матрицы X случайным образом исключается часть измеренных значений, затем исключенные пропуски заполняются. Мера качества заполнения определяется с помощью меры заполнения истинных значений от полученных.

Анализ выбросов

При наличии таких данных возникает вопрос: чем объяснить обнаруженные резкие отклонения в исходных данных? Например, объясняются ли они природой анализируемой генеральной совокупности? Если случайные колебания выборочных значений обусловлены искажениями стандартных условий сбора статистических данных или прямыми ошибками регистрации и записи, то их надо исключить. Наиболее надежным способом решения вопроса об исключении данных из рассмотрения является изучение условий регистрации и сбора данных. Если невозможен анализ условий, при которых регистрировалось аномальное наблюдение, то обращаются к статистическим методам. Их общая логическая схема: исходя из исходных предложений о природе анализируемой совокупности данных, исследователь задается функцией (- все имеющие наблюдения, - подозрительные наблюдения), характеризующей степень аномальности, определяет значение и сравнивает с пороговым значением . При подозрительное наблюдения исключается, или для него определяется весовой коэффициент. В вероятностной постановке определяется из стандартных статистических таблиц с учётом закона распределения статистики в предположении необоснованности относительно . В других случаях определяется из содержательных соображений.

Проверка гипотез

Статистические процедуры анализа резко выделяющихся наблюдений основаны на предположении однородности данных. При этом выбросы рассматриваются как наблюдения, нетипично удаляющиеся от центра распределения. Основная трудность при использовании имеющихся аналитических процедур состоит в том, что реальная доля «засорения» не известна, а оценивается по тем же данным, по которым проверяется значимость отклонения. Наиболее устойчивы к отклонениям от предположения нормальности основной части выборки графические процедуры. При использовании статистических методов выделения выбросов следует иметь в виду, что выбросы могут оказаться наиболее существенной частью выборки, проясняющей, например то, как собирались данные (например, изменение условий эксперимента, не замеченное исследователем). Данная задача распадается на два этапа: выделение подозрительных наблюдений; проверка статистической значимости отличий от основной массы данных. Оба этапа основываются на определенных предположениях о распределении основной (не засоренной) части наблюдений и выбросов (засорений). Обычно предполагают, что не засоренная часть наблюдений имеет одно или многомерное нормальное распределение с неизвестными параметрами , а засоренная: или .

Унификация признакового описания

Отношение, признаки, измерения

Для описания разнородных задач первичной статистической обработки помимо обычного языка математической статистики удобно использовать терминологию теории бинарных отношений. Опишем кратко основные понятия.

Отношения. Бинарное отношение Р на множестве объектов - подмножество упорядоченных пар объектов (а, в) декартового произведения на : .

У некоторых особо важных отношений есть специальные названия.

Отношение эквивалентности разбивает все множество объектов на не пересекающиеся классы, в каждом из которых объекты признаются тождественными, неразличимыми, а из разных классов – нетождественными.

Квазипорядок (нестрогий порядок) определяет отношение «быть не меньше». Если исключить из него возможность равенства элементов, то оно превратится в порядок.

Толерантностью называется отношение «похожести». В анализе данных оно имеет особую роль, так как объединение объектов происходит по похожести. Здесь в отличие от эквивалентности из а=в, в=с не следует а=с.

Метризованное отношение. Каждому отношению на множестве объектов можно сопоставить матрицу из бинарных значений r_ij={0,1}, где для, иначе. Понятие «отношение « можно расширить, распространив его на количественные признаки. В 1977 Б. Г. Литваком введено понятие «метризованного отношения». «Метризованным отношением» называется пара <W(Р),Р> , где Р – отношение, W(Р) – множество чисел (весов), характеризующих «степень принадлежности» пары к данному «метризованному отношению». Вместо булевских матриц (2.2) вводятся матрицы с вещественными элементами , которые определяются (для линейных отношений порядка).

Признаки. Отношения определены на парах объектов. Признак – это свойство, измеренное на каждом объекте. Может случиться, что отношение существует, а измеримые признаки им не отвечают. Так, отношению толерантности нельзя сопоставить признак, определенный на каждом объекте.

Измерение. Рассмотрим способы измерения признаков. Обычно под процедурой измерения какого-либо свойства понимается приписывание некоторых числовых значений отдельным уровням этого свойства в определенных единицах. При этом важно знать в какой мере условность в выборе единиц измерения повлияет на значение показателя. Например, если стоимость продукции измерить в рублях, а потом в тысячах рублей, то изменится лишь число единиц измерения, суть же останется прежней. Здесь возможно умножение, деление на константу, т. Е. масштабирование. Бессмысленно задавать масштаб для температуры по Цельсию, так как мы не можем сказать во сколько раз -5 меньше +10. Таким образом разные типы признаков имеют разное множество допустимых преобразований своих значений, которое определяет тип шкалы.

Типовые структуры признаков

Признаки, описывающие объекты получаются по-разному. В зависимости от того, как измеряют или оценивают значение признака, они могут быть первичными или вторичными. Замер берётся за значение признака. Можно выделить шесть типов признаков:

К первому типу относится прямое измерение, т.е. измерение с использованием приборов (например, измерение длины стола линейкой, измерение скорости машины спидометром, измерение температуры воздуха градусником, измерение силы тока амперметром, измерение глубины моря тахометром и т.д.) или при помощи счета (например, сосчитать количество книг на полке, количество фруктов в ящике, количество рыб в аквариуме и т.д.).

Ко второму типу относится прямое измерение с последующим аналитическим преобразованием, зависящим от параметров (они вносят случайный разброс в значение). Это измерение подразделяется на одноуровневое, т.е. измерение на объекте и двухуровневое – на группе объектов (например, измерение дозы облучения – человека помещают в некоторую камеру, где одновременно измеряется его вес, количество радиационных частиц, содержащихся в нем и получают представление о дозе внутреннего облучения).

К третьему типу относится аналитическая комбинация: нескольких первого типа или нескольких первого и второго типов (характеристика группы людей – имеется некоторое количество детей в группе, известен их вес, рост, нужно определить средние характеристики по группе, например, средний вес, процент девочек в группе).

К четвёртому типу относится прямая экспертная оценка (например, уровень подготовленности студента, пригодность продуктов для употребления, возможность использования природных ресурсов и т.д.).

К пятому – прямая экспертная оценка с последующим аналитическим преобразованием (например, в зависимости от компетентности эксперимента, т.е. от степени доверия к оценке, полученной экспертом, получается результирующая оценка путём умножения исходной оценки на некоторый коэффициент, который является функцией от компетентности).

К шестому – аналитическая комбинация экспертных оценок (например, берётся несколько экспертных оценок и у каждой есть своя компетентность, и вычисляется средняя оценка).

Типы шкал

Интегрированная информация о шкалах приведена в таблице 10.1.

Таблица 10.1 – Интегрированная информация о шкалах

Наименование шкалы	Множество допустимых преобразований F(x)	Отношения, отвечающие шкале	Допустимые числовые операции с измерениями	Примеры измерения
Качественная шкала
Наименований (номинальная, классификационная)	Взаимно-однозначные	Эквивалентность	Сравнения: x=y, x<>y	Национальность, пол, профессия, вид оплаты труда
Порядковая (ранговая, ординальная)	Монотонно-неубывающие функции	Квазипорядок (нестрогая ранжировка)	Сравнения: x<=y	В строгом смысле примеров шкалы нет. Условно: шкала твердости минералов, экспертные ранжировки, оценки предпочтений
Количественная шкала
Разностей (балльная)	F(x)=d+x	Аддитивное метризованное	Сравнения: x-y<=z-v; x+y, x-y	Квалификационные разряды, балльные оценки
Интервалов (интервальная)	F(x)=d+kx, k>0	4-арное мультипликативное метризованное	(x-y)/(z-v), x+y, x-y	Любые показатели, значения которых могут быть отрицательными: температура по Цельсию, летоисчисление, прибыль (при наличии убытков), высота над уровнем моря
Отношений (относительная)	F(x)=kx, k>0	Мультипликативное метризованное	X/y, x*y, x+y, x-y	Температура по Кельвину, возраст, производительность труда

Шкалы. Отображение , называется шкалой наименований, если его допустимым преобразованием является взаимно однозначное отображение . Шкальные значения играют роль имен объектов. Здесь определено отношение равенства, которое соответствует отношению эквивалентности. Оно индуцирует на А разбиение на непересекающиеся классы. Эти признаки называют классификационными или номинальными. Примеры: профессия, национальность, пол, место рождения.

Отображение называется шкалой порядка, если его допустимым преобразованием является монотонно возрастающее непрерывное отображение . Определены отношения равенства и порядка. Первое соответствует эквивалентности объектов, второе - порядку. Отношение эквивалентности индуцирует разбиение А на классы, а отношение порядка задает линейный порядок на множестве классов эквивалентности. Соответствующее отношение порядка задает порядок на множестве различных значений признака , которые называются градациями шкалы порядка. Эти признаки называют порядковыми или ординальными. В строгом смысле примеров шкалы нет. Условно примерами шкалы являются: сила ветра в баллах, образование, оценка на экзамене, шкала твердости минералов.

Отображение называется количественной шкалой: а) интервалов; б) отношений; в) разностей; г) абсолютной, если допустимым преобразованием является положительное линейное преобразование вида:

,

где для каждого подвида количественной шкалы а); б); в); г). Примеры: а) любые показатели, значение которых может быть отрицательным: температура по Цельсию, летоисчисление, убытки - прибыль; б) возраст, вес, длина; в) квалификационные разряды, балльные оценки; г) количество элементов некоторого множества, адрес в памяти ЭВМ.

Унификация типа переменных

Одна из сложностей автоматизированного анализа информации заключается в том, что среди признаков могут быть количественные и качественные (порядковые или классификационные), а большинство методов статистической обработки предполагают их однотипность. Поэтому и возникает вопрос об унификации записи единичного наблюдения.

1-й вариант решения. Наблюдение представляют в виде вектора размерности , - число градаций (интервалов группирования, уровней качества или однородных групп) признака . Компоненты этого вектора принимают значение 0 или 1. Недостатки: субъективизм в выборе способов разбиения диапазонов количественных признаков, потеря информативности при переходе от индивидуальных к групповым значениям.

2-й вариант. Преобразование качественных переменных в количественные с помощью «оцифровки» (шкалирование).

3-вариант. Сведение классификационных и количественных данных к порядковым.