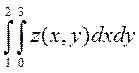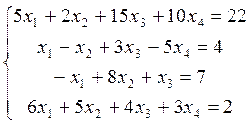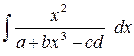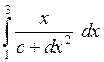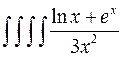Для работы с матрицами удобно
пользоваться следующими функциями:
·
ones –
формирование массива из единиц;
·
zeros –
формирование массива из нулей;
·
eye –
формирование единичной матрицы;
Вернуться назад к содержанию
·
rand –
формирование массива из чисел, случайно распределённых на отрезке [0, 1];
·
randn –
формирование массива из чисел, нормально распределённых на отрезке [0, 1];
·
magic – формирование
магического квадрата;
·
pascal – формирование
квадрата Паскаля;
·
diag – диагональная
матрица;
Рассмотрим
основной синтаксис на примере функции создания единичной матрицы (eye). С помощью функции eye(m) можно создать единичную матрицу размера [m, m], а с помощью функции
eye(m, n) единичную
матрицу размера [m, n]. При этом «лишние» строки или столбцы дополняются
нулями.

Функция zeros(m, n) – создает матрицу размером m на n с
нулевыми элементами, а команда ones (m, n) - создает
матрицу размером m на n с единичными элементами.

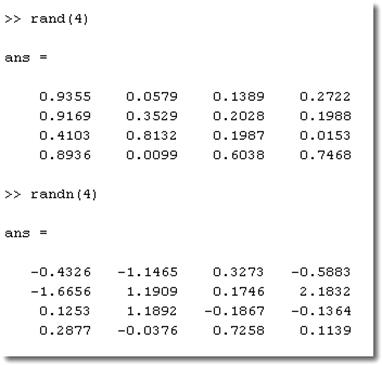
Функция
rand (m,n) - создает матрицу размером m на n из случайных
чисел, равномерно распределенных в диапазоне от 0 до 1.
Вернуться назад к содержанию

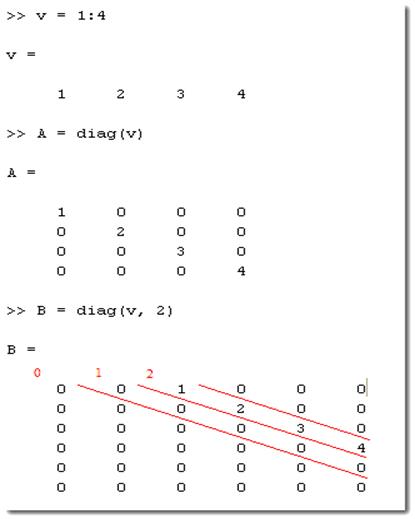
Функция diag используют для работы с диагональными матрицами, у
которых ненулевые элементы расположены на диагоналях. Синтаксис:
·
X = diag(v) – на главной
диагонали матрицы X расположены элементы вектора v;
·
X = diag(v,k) – на k-ой диагонали
матрицы X расположены элементы вектора v (по умолчанию k=0);
·
v = diag(X,k) – извлечь из матрицы X k-ую диагональ и
сохранить её в векторе v. Вернуться назад к
содержанию
Над элементами массивов можно совершить
следующие простейшие операции:
·
sum- находит сумму элементов;
·
prod- находит
произведение элементов;
· cumsum- находит кумулятивную сумму элементов;
·
cumprod:
кумулятивное произведение элементов;
·
max- находит максимальный элемент;
·
min- находит
минимальный элемент;
· sort- сортируют элементы.
Рассмотрим работу некоторых из этих
функций на примерах. Для векторов функция sum возвращает сумму элементов. Для массивов – сумму
элементов по каждому из столбцов. Результатом является вектор-строка. Остальные функции работают по
этому же принципу. Вернуться назад к содержанию
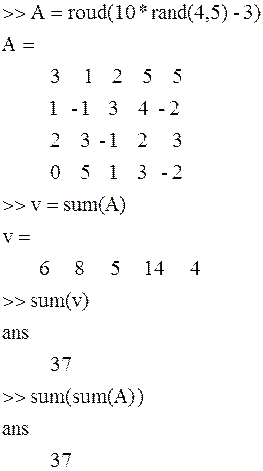
Кумулятивная сумма вычисляется так же, только
происходит накопление вычисленных значений в элементах массива.
 Вернуться назад к содержанию
Вернуться назад к содержанию
Максимальный и
минимальный элементы определяют следующим образом:

Вызов
функций max/min с двумя
выходными параметрами позволяет определить и индекс найденного элемента:
Вернуться назад к содержанию

Функция sort производит сортировку элементов матрицы по столбцам:

Функция All(v) –
возвращает истину, если все элементы вектора v отличны от нуля. Для
матриц выдаёт вектор-строку с аналогичным результатом для каждого
столбца: Вернуться
назад к содержанию

Функция Any(v) –
возвращает истину, если хотя бы один элемент вектора v отличен от нуля. Для
матриц выдаёт вектор-строку с аналогичным результатом для каждого
столбца:

Функция find определяет индексы элементов, удовлетворяющих
заданному условию:

Функция det вычисляет
определитель квадратной матрицы.
При
работе с матрицами можно использовать два вида операторов:
·
матричные- производят действия по правилам матричной алгебры;
·
поэлементные- производят действия над соответствующими элементами
матриц. При этом размеры матриц должны быть одинаковыми. От матричных операций
отличаются точкой перед знаком операции.
Матричные
и поэлементные операции:
•
‘ транспонирование;
•
+ матричное (и поэлементное) сложение;
•
- матричное (и поэлементное) вычитание;
•
* матричное умножение;
•
/ матричное деление;
•
^ матричное возведение в степень;
•
\ матричное
деление «слева»;
•
.* поэлементное умножение;
•
./ поэлементное деление;
•
.^ поэлементное возведение в степень;
Вернуться назад к содержанию
•
.\ поэлементное
деление «слева.
Операции «деления» слева и справа применяются для решения систем линейных
уравнений (СЛУ). Деление слева (\) для квадратных матриц реализует метод Гаусса,
а для прямоугольных матриц– метод наименьших квадратов.
Пример. Найти сумму и разность матриц:
>>А=[1 2 3 4 5; 6 7 8 9 11]
A= 1 2
3 4 5
6
7 8 9 11
>>B=[0 -1 -2
-3 -4; 5
6 7 8 9]
B = 0 -1 -2
-3 -4
5 6 7
8 9
>>A+B
ans = 1
1 1 1
1
11
13 15 17 20
>>А-B
ans = 1 3
5 7 9
1 1 1 1 2
Пример. Найти
произведение матрицы на число
>>А*5
ans = 5
10 15 20 25
30
35 40 45 55
Пример.
Транспонирование матрицы
>>А’
ans = 1 6
1
7
2
8
3
9
4
11
Пример.
Найти произведение двух матриц
>>A’*B
ans = 30 35 40
45 50
45
40 45 50 55
40 45
50 55 60
45 50
55 60 65
50 61
67 73 79
C помощью функции
inv (A) находят матрицу обратную заданной матрице А. При этом исходная матрица А должна быть
квадратной и её определитель должен быть отличен от нуля.
Весьма интересными в языке Matlab являются операции деления матриц слева направо и
справа налево .(/ и \)
Операция
А\В равносильна совокупности
операций inv(A)*B, которая является решением матричного уравнения: А*Х=В.
Для
примера рассмотрим решение системы линейных алгебраических уравнений:
x1 + 2x2 +
3x3 = 14
2x1 - x2 -
5x3 = -15
x1 - x2-
x3 = - 4
Вводим
матрицу коэффициентов А и вектор строку В:
>>A=[1 2 3; 2 -1 -5; 1 -1 -1]
A= 1 2 3
2
-1 -5
1
-1 -1
>>B= [14; -15; -4]
B = 14
-15
- 4
>>x = A \ B
x =
1
2
3
То есть x1 =1 x2 =2 x3 = 3 –
корни системы уравнений.
В
системе Matlab предусмотрены возможности математического оперирования с полиномами.
Полином (многочлен) как функция определяется
следующим выражением:

В Matlab полином задается и хранится
в виде вектора, элементами которого являются коэффициенты полинома от an до а0
P = [an … a2 a1 a0]
Ввод
полиномов осуществляется также как и ввод вектора длиной n+1, где n – порядок
полинома.
Система
Matlab имеет функцию roots(P) которая
вычисляет вектор, элементы которого являются корнями заданного полинома, по
вектору коэффициентов. Пусть требуется найти корни полинома:
Р(х) = х5+8x4+31x3+80x2+94x+20
>>P=[1
8 31 80
94 20]
>>roots(P)
ans=
-1.0000+3.0000i
-1.0000+3.0000i
-3.7321
-2.0000
-0.2679
Обратная
операция – построение вектора Р
коэффициентов полинома по заданному вектору его корней – осуществляется
функцией poly.
P = poly(R),
где R – заданный вектор корней полинома, Р – вычисленный вектор
коэффициентов полинома.
Пример:
>>P = [1 8
31 80 94
20]
ans =
1
8 31 80
94 20
>>R= roots (P)
ans =
-1.0000+3.0000i
-1.0000+3.0000i
-3.7321
-2.0000
-0.2679
>>P1 = poly(R)
ans=
1.0000
8.0000 31.0000 80.0000
94.0000 20.0000
Для вычисления значения
полинома по заданному значению его аргумента в Matlab предусмотрена функция polyval. Обращение к ней происходит по схеме:
y = polyval (Р, x),
где Р –
вектор коэффициентов полинома, x – значение
аргумента полинома.
Пример.
>>P = [1 8
31 80 94
20]
>>x = 2
>>y = polyval (P, x)
ans=
936
Вычисление производной от полинома производится функцией polyder. Эта функция создает вектор коэффициентов полинома
представляющий собой производную от заданного полинома:
>>dp = polyder (P)
dp = 5 32 93
160 94
Вернуться назад к содержанию
Перейти к лабораторной работе 2
3. Графика в Matlab
В среде Matlab имеется высокоуровневая, объектная и управляемая
графика. Графика Matlab не
требует от пользователя детальных знаний о работе графической подсистемы, каждый
объект на рисунке имеет свойства, которые можно менять и доступ к графическим
объектам возможен как через инспектор объектов, так и при помощи встроенных
функций.
Для
построения 2D-графика необходимо задать
область построения (диапазон), вычислить значение функции на области построения
и построить график при помощи одной из встроенных функций Matlab.
Например:

Если
сразу же построить другой график, то старый график будет удалён из графического
окна. Для построения двух графиков в одной СК необходимо «закрепить»
графическое окно при помощи команды hold on и применить
одну команду plot.
Например:
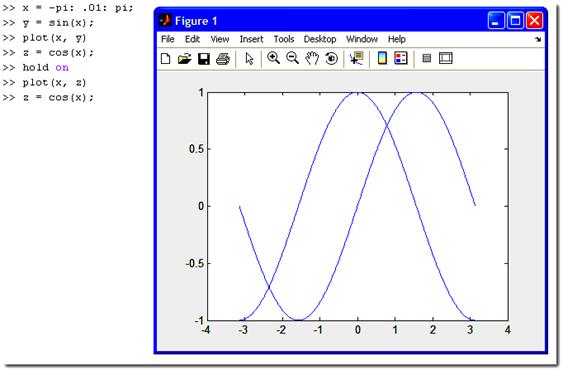
А
также два графика в одной СК можно построить с помощью дополнительных
параметров команды plot.
Например:
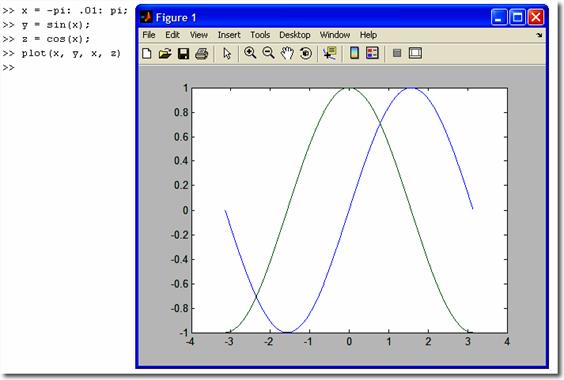
В
команде plot можно задать для каждого
графика цвет линии, тип маркера и тип
линии

Например:
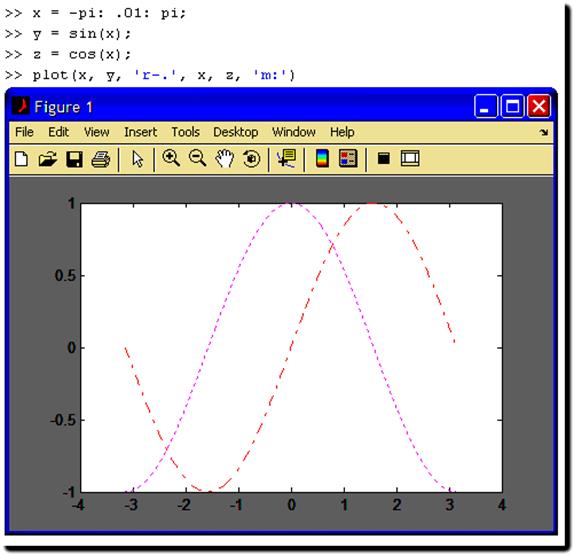
В среде Matlab имеется возможность построения нескольких графиков в
одном окне но в разных системах координат. Для этого поверхность графического
окна с помощью команды subplot
можно разделить на зоны, в каждой из которых выводится график. В качестве
параметров ей передаётся трёхзначное целое число вида mnk (m и n определяют количество графических «подокон» по
горизонтали и вертикали, а k задаёт номер
графического «подокна»). При этом порядок нумерации - по строкам.
Например:
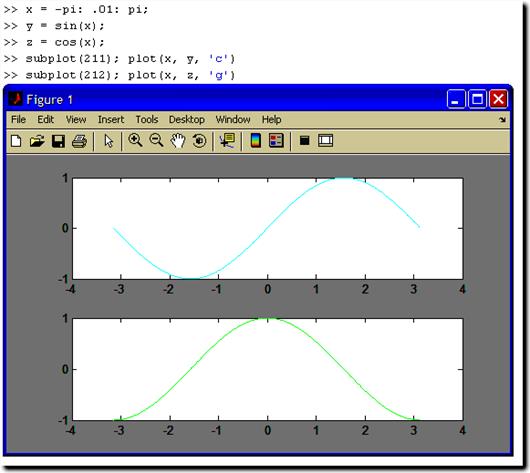
Для построения графиков в разных графических
окнах нужно создать новое графическое окно с помощью команды figure. Команда figure создаёт графическое окно и возвращает указатель на
него: h = figure, а активизировать ранее созданное
окно можно командой figure(h).
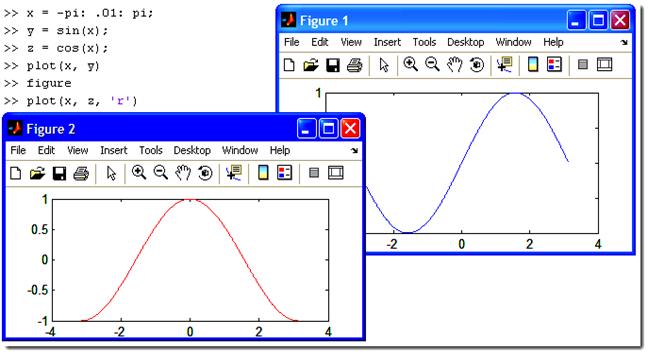
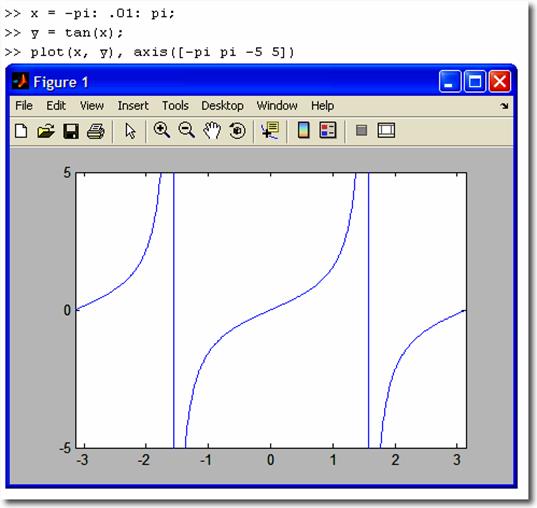
В среде Matlab для управления масштабом
имеется команда Axis. Команда axis([Xmin Xmax Ymin Ymax]) задаёт область построения графиков по осям X и Y.Команда используется,
если результат автомасштабирования неудовлетворителен.
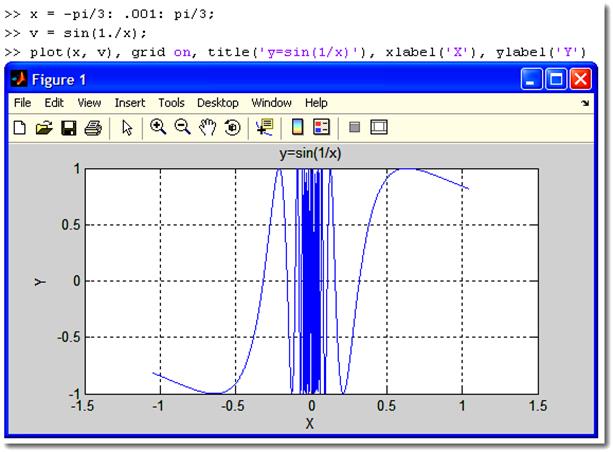
Для
графиков можно задать масштабную сетку с помощью команды grid on, заголовок с помощью команды title(’заголовок’),
подписи осей координат с помощью команды xlabel(’текст’) и
ylabel (’текст’). В заголовках и подписях можно использовать
нотацию системы TeX.
А
также в Matlab можно
построить графики функций, заданных в параметрическом виде. Строятся они при
помощи оператора plot. Для этого вначале задаётся диапазон построения t, затем
вычисляются x(t) и y(t) и строится график. Графики параметрических функций
часто возникают в физических приложениях. Независимая переменная t в этом случае имеет смысл времени, а x и y –
координаты. Для построения динамического графика можно использовать функцию comet(x,y).
Пример 1 (оформление графика).
Пример 2 (Графики функций,
заданных в параметрическом виде).

Графики
в полярной системе координат строятся аналогично графикам функций в декартовой
системе. Для построения используется команда polar.
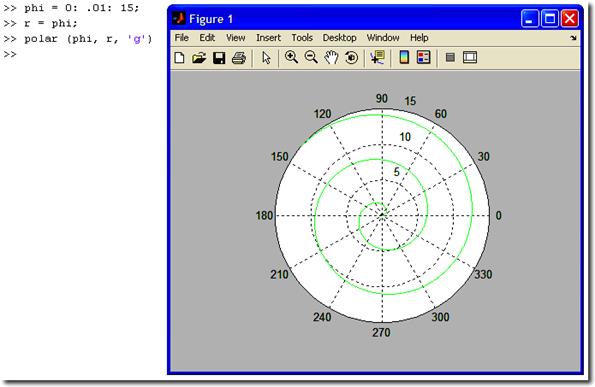
Графическое
представление функции в виде ступенчатого графика осуществляется с помощью
функции stairs (x, y). Для этого сначала
надо для значений аргумента x нужно сформировать
массив, а затем осуществить вывод функции в виде ступенчатого графика
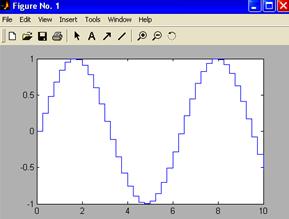
Пример:
x = 0:.25:10;
stairs (x,sin(x))
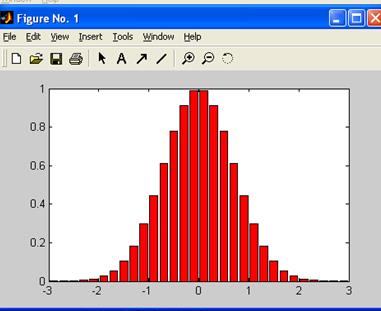
В среде Matlab можно
также построить график функции в виде столбчатой диаграммы. Это осуществляется
с помощью функции bar(x, y)
x =
-2.9:0.2:2.9;
bar(x,exp(-x.*x))
colormap
hsv
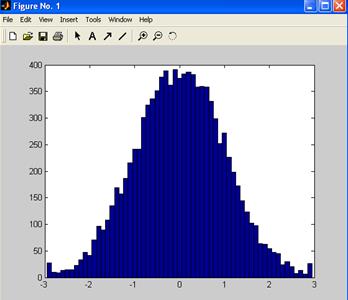
Другим примером является построение графика в
виде гистограммы. Это осуществляется с помощью функции hist(y, х)
Построим гистограмму случайных величин,
которые формируются функцией randn.
x = -2.9:0.1:2.9;
y= randn(10000,1);
hist(y,x)
Система Matlab имеет очень
большие возможности построения трехмерных графиков. В Трёхмерную (3D-) графику Matlab
входит построение:
· поверхностей
· контурных диаграмм (линии равного уровня)
· 3D-линий
· векторных полей
· скалярных полей
· и др.
Мы рассмотрим только несколько функций,
позволяющих создавать трехмерные графики.
Для построения трехмерного графика z = f(x, у) необходимо иметь матрицы значений переменных х,
у. Для определения матриц предназначены следующие функции:
[X,Y] = meshgrid (x, у);
[X,Y] = meshgrid (x);
[X,Y,Z] = meshgrid (x, у, z);
Функция
[X,Y] = meshgrid(x,y) — преобразует область векторов х, у в массивы X, Y, которые
используются для вычисления функции z = f(x, у) и построения графиков.
Строки массива Х являются копиями вектора х, а
столбцы массива Y - копиями вектора у.
Функция [X,Y,Z] = meshgrid(x, у, z) возвращает трехмерный массив для построения
трехмерного графика.
Графики трехмерных поверхностей строятся с
помощью следующих функций:
plot3 (x, у, z),
plot3 (X, Y, Z),
plot3 (X, Y, Z, s),
plot3 ( x l , yl, zl, s1, x2, y2, z2, s2, . .
. , xn, yn, zn, sn),
где x, у, z — векторы
аргументов функции, Х, Y, Z — матрицы одинакового
размера, s— стили линий и точек графика,
аналогично функции plot ().
Приведенные функции строят точки трехмерного
графика и соединяют их отрезками прямых в соответствии с заданным стилем.
Функция plot3(xl,yl,zl,sl,x2,y2,z2,s2,...,xn, yn, zn,sn) строит на одном рисунке n функций.
Пример. Построить график функции z = ln х + ln у в диапазоне
аргументов [-4; 4] с шагом h = 0.1.
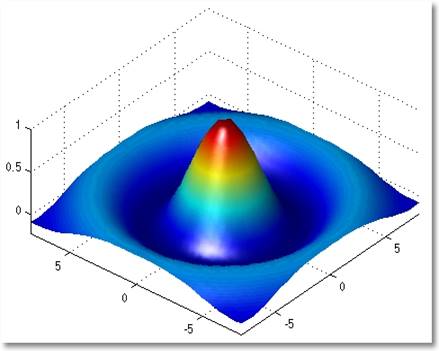
Рассмотрим пример построения поверхности f(x,y)=sin(r)/r, где r=sqrt(x2+y2).
Вернуться
назад к содержанию
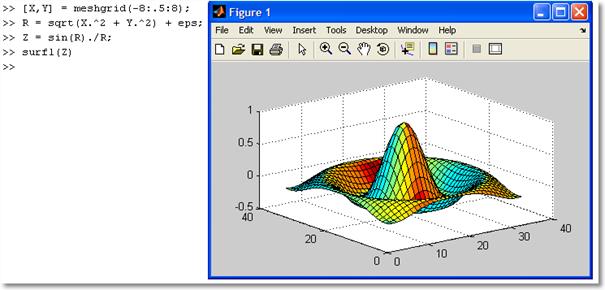
Функции
для построения поверхностей:
|
Функция
|
Для
чего используется
|
|
mesh, surf
|
Построение
поверхностей
|
|
meshc, surfc
|
Строит
поверхность и контурную диаграмму под ней
|
|
meshz
|
Поверхность
на «пьедестале»
|
|
surfl
|
Подсвеченная
поверхность
|
|
contour
|
Контурная
диаграмма
|
|
plot3
|
Трёхмерная
линия (параметрическое задание)
|
|
comet3
|
Движение
по трёхмерной линии
|
О других графических функциях можно узнать
в системе помощи Matlab.
Вернуться назад к содержанию
Перейти к лаборатоной работе 3
4. Программирование в Matlab
Написание программ – это
альтернатива работе в командной строке. Программный код Matlab размещают в файлах с расширением «m» (m-файлах). m-файлы бывают двух видов:
–
скрипты (scripts);
–
функции (functions).
К сожалению, Matlab плохо понимает кириллицу…
Скрипты представляют собой
последовательности команд Matlab, как если
бы мы перенесли их из командного окна в отдельный файл. Скрипт вызывается по
имени через командную строку и выполняется в режиме интерпретатора, и они полезны для автоматизации
последовательности действий, которые выполняются многократно. Скрипты не могут
принимать параметры и возвращать аргументы. Они хранят значения своих
переменных в рабочем пространстве, где переменные доступны для других скриптов
и из командной строки.
Функции- это специальный вид m-файлов. В отличие от скриптов могут принимать
аргументы и возвращать значения. Использование функций позволяет структурировать
программу и избежать повторения кода.
Создание функции преследует целью
расширение языка. Переменные, определённые внутри функции являются локальными,
то есть видны только внутри самой функции. Функция имеет собственное имя. Кроме
того, с ней связано имя m-файла, в
котором функция записана. При этом будем соблюдать правило: имя функции и имя m-файла должны быть одинаковы.
Функция состоит из заголовка и тела
function f = fact(n) Заголовок
% Вычисляет
факториал. Линия H1
% FACT(N) возвращает N!, Help
f = prod(1:n); Тело
функции
При этом H1 и Help выводятся по команде
help <имя функции>. Фактически, функция отличается
от скрипта наличием заголовка и способом вызова.
Function f = fact (n)

Вернуться назад к содержанию
Комментарии используются для пояснения кода и временного
исключения
кода из текста. Они могут быть строчными и блочными. Строчные
начинаются с символа «%». С этого места и до конца строки всё игнорируется
компилятором %. Блочные начинаются с символа «%{» и заканчиваются символом «%}»
При этом эти символы должны обязательно стоять в отдельных строках.
Можно автоматически закомментировать
блок текста. Для этого нужно:
–
выделить блок;
–
щёлкнуть правой
кнопкой;
–
выбрать Comment (или Ctrl+R).
Для снятия
комментарий нужно:
–
выделить
закомментированный блок;
–
щёлкнуть правой кнопкой;
– выбрать Uncomment (или Ctrl+T).
Создать m-файл можно в любом
текстовом редакторе, например, во встроенном редакторе при помощи меню или
командой edit <имя файла>.

Функция вызывается по своему имени (которое
совпадает с именем её m-файла).

Вернуться назад к содержанию

При написании функций в Matlab можно
проводить проверку количества входных и выходных параметров. Для этого в
описании функции используют служебные слова:
·
nargin- количество входных параметров;
·
nargout- количество выходных параметров.
В файлах-функциях Matlab могут быть реально описаны несколько функций. Синтаксически
это оформляется как две (или более) функций, записанных в одном файле. При
вызове такого m-файла происходит запуск самой
первой функции. При этом её имя должно совпадать с именем файла. Описание
следующих функций локально. Обычно они используются как вспомогательные для
первой функции.

Вернуться назад к содержанию

При вызове m-файла сравнительно много времени тратится на его
компиляцию. Чтобы сократить время выполнения можно предварительно перевести m-файл в p-код («пи-код»)
с помощью команды pcode <имя m-файла>. Откомпилированный
в псевдокод файл получает расширение «p». Такой
файл будет выполняться быстрее, чем обычный m-файл.
Интерактивный ввод данных используется
при написании скриптов. Для ввода числовых данных применяют функцию input по формату x = input(’строка
приглашения’). Введённое
пользователем значение сохранится в переменной x. Для ввода строковых данных функция input
вызывается с дополнительным параметром: c = input(’строка
приглашения’,’s’). Кроме того, имеется Си-подобная функция sscanf.


Для вывода данных в командное окно
используют команду disp (от display)
по формату disp(<выводимая
строка>). Если выводимое значение
– число, то вначале его преобразуют к строковому типу при помощи функций int2str или num2str. Конкатенацию
строк производят как для одномерных векторов-строк.

Кроме
того, имеется Си-подобная функция sprintf.
Как и любой процедурный язык
высокого уровня, Matlab позволяет использовать при
написании программ:
·
следование,
·
ветвление,
·
циклы,
·
пользовательские
функции.
Следование
реализуется перечислением каждого из операторов в отдельной строке, либо в
одной строке через запятую (или точку с запятой).
Ветвление
реализуется в двух вариантах:
– при помощи оператора if,
–
при помощи
оператора switch.
Простейшая форма оператора if:
if <логическое выражение>
<операторы>
end

В полном варианте оператора могут
использоваться слова else и elseif. Слово elseif может использоваться в одном операторе многократно с
указанием условия. Слово else – только один раз в конце оператора и без условия.
Вернуться назад к содержанию

Циклы.
В Matlab имеется два вида циклов:
· цикл с параметром for,
· цикл c предусловием while.
А также
имеются оператор досрочного выхода из цикла break и оператор перехода к следующей итерации continue.
Циклы с параметром имеют вид:


 Обычно цикл for используется для обработки массивов. Важно помнить,
что если есть возможность обойтись без этого цикла (применить матричные или
векторные операции), то лучше избавиться от явного цикла. В этом
случае программа будет работать на порядок быстрее.
Обычно цикл for используется для обработки массивов. Важно помнить,
что если есть возможность обойтись без этого цикла (применить матричные или
векторные операции), то лучше избавиться от явного цикла. В этом
случае программа будет работать на порядок быстрее.
Пример.
Замена отрицательных элементов вектора на нули
(с циклом).

Цикл с
предусловием имеет вид:
while <логическое выражение>
<операторы>
end
Операторы
выполняются, пока логическое выражение есть истина (true).

Операторы break и continue аналогичны одноимённым
операторам Паскаля. Оператор break производит досрочный выход из цикла for или while, а continue
прекращает выполнение текущей итерации и переходит к следующей.
Напишем скрипт, который вводит с
клавиатуры произвольное количество чисел. Если число положительное, то оно прибавляется
к сумме, если отрицательное, то пропускается. Ноль – признак окончания работы.

Выход из
функции в вызывающую
программу обеспечивается выполнением последнего ее оператора или командой return.
Кроме упомянутых основных операторов, традиционных для любой системы
программирования, остановимся на ряде операторов обеспечения пользовательского
интерфейса.
Приостановка выполнения программы может быть предусмотрена
включением в текст команды:
pause (приостановка до нажатия
любой клавиши),
pause (n) (приостановка на n сек),
keyboard (приостановка с
возможностью выполнять практически любые команды и последующим возвратом в
программу командой return).
Можно построить выбор варианта с клавиатуры созданием
меню:
<переменная>=menu(‘заголовок’,’выбор1’,’выбор2’,...)
Например, команда:
k=menu(‘Использовать
метод’,’Гаусса’,’Краута’,’Простой итерации’) создаст на экране всплывающее меню с указанными пунктами
клавишами и щелчок по клавише задаст значение переменной k, равное 1, 2 или 3.
Вернуться назад к содержанию
Перейти к лабораторной работе 5
5. Аналитические вычисления в Matlab
Изначально Matlab имел средства только для численного анализа. Сегодня
в Matlab встроены средства аналитических (символьных)
вычислений. Symbolic Math Toolbox- является вычислительным ядром системы Maple V. Установка
Maple не требуется.
Для символьного анализа в среде Matlab требуется создать символьные переменные и функции. Символьные
переменные создаются по одной переменной x=sym(’x’). Так же можно создать целое символьное выражение syms x y z. Символьные
функции определяются через символьные переменные f=x^2+y. Для построения символьных функций можно
воспользоваться командой ezplot. Представить в стандартной форме можно с помощью команды
pretty.

Вернуться назад к содержанию

В
системе Matlab имеются следующие символьные вычисления: преобразования и
анализа (дифференцирование, пределы, интегрирование, разложение в ряд Тейлора),
упрощения и подстановки, точной арифметики, линейной алгебры и решения
уравнений и их систем (обычных и дифференциальных).
Символьное вычисление пределов (сводная
таблица).

Символьное вычисление интегралов (сводная
таблица).

Рассмотрим некоторые из них на примерах.
Пример. Символьное вычисление пределов.

Пример.
Символьное вычисление односторонних пределов.
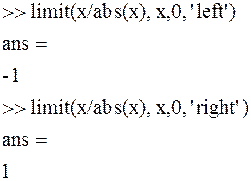
Пример.
Символьное дифференцирование.
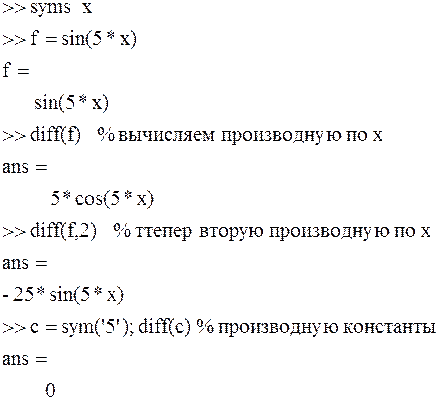
Пример.
Символьное вычисление частных производных.

Пример.
Символьное разложение в ряд Тейлора.
Вернуться назад к содержанию

Пример. Нахождение экстремума функции.

Построение экстремумов функции.
Вернуться назад к содержанию

В системе Matlab операции над полиномами реализуются при помощи
функций collect, expand, factor, horner. Операция collect – вычисляет коэффициенты при степенях независимой
переменной (по умолчанию – x). Можно
явно задать имя независимой переменной в виде: collect (f, VarName).

Операция expand – представляет полином суммой степеней без приведения
подобных.

Операция factor – разлагает полином на множители, если эти множители
имеют рациональные коэффициенты.

Операция simplify реализует мощный алгоритм упрощения с использованием
тригонометрических, степенных, логарифмических, экспоненциальных функций, а
также спецфункций (Бесселя, гипергеометрической, интеграла ошибок и пр.), а
операция simple пытается получить выражение, которое представляется
меньшим числом символов, чем исходное, последовательно применяя все функции
упрощения Symbolic Math Toolbox. Иногда
simple даёт более удачное решение, чем simplify


Операция simple особенно эффективна при работе с тригонометрическими
выражениями.

Операция subs
подставляет одно символьное выражение в другое. Общий формат операции имеет
вид:
–
subs(<куда>,
<вместо чего>, <что>)
Подстановка вместо переменной её
числового значения приводит к вычислению символьной функции от значения
аргумента.
Рассмотрим пример подстановки:
Вернуться назад к содержанию

В системе Matlab точные
вычисления реализуются функцией vpa
(Variable-Precision Arithmetic). Формат вызова функции имеет вид:
–
vpa(<выражение>, <значащих цифр>)
–

В системе Matlab решение уравнений и систем выполняет команда solve. До 4-го
порядка включительно решаются точно. Ответ выводится в степенях рациональных
чисел. Уравнения высших порядков и трансцендентные, как правило, точно не
решаются и в этом случае выводится приближённый результат. С целью сокращения
записи при выводе могут использоваться подстановки.

Решение систем также выполняет команда solve. При этом входные
аргументы левые части уравнений, переменные, по которым нужно разрешить систему,
например: s = solve(f1, f2, x1, x2). Выходной аргумент структура (запись) s с полями (в данном случае) x1 и x2, хранящими
символьное представление решения.
Вернуться назад к содержанию
6. Алгоритмы и технологии численного
вычисления в системе Matlab
Система
Matlab имеет большое число способов численного
интегрирования. Численное интегрирование необходимо в следующих случаях:
•
первообразная не выражается через элементарные функции;
•
аналитическое выражение интеграла слишком сложное;
•
подынтегральная функция задана в табличной форме или в виде матрицы.
При
вычислениях интегралов численными методами подынтегральную функцию
целесообразно представлять в наиболее простом виде. Это может ускорить
вычисления. Упрощение подынтегральной функции можно выполнить, воспользовавшись
функцией simplify(y).
Имеют
место случаи, когда система до упрощения не может вычислить неопределенный
интеграл и легко его определяет после упрощения.
Метод
вычисления интеграла выбирает пользователь. В этом особенность системы MATLAB.
С помощью MATLAB студент имеет возможность сравнивать различные методы
численного интегрирования.
Существует
ряд способов численного интегрирования. Во всех таких способах вычисление
осуществляется по приближенным формулам, называемым квадратурными. Приведем
некоторые из них.
Формулы прямоугольников. Формулы
прямоугольников представляются в следующем виде:
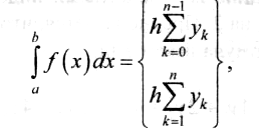
где: h — шаг интегрирования, уk — значение подынтегральной функции при аргументе хk, k=0,1,2,..., n и n=(b-a)/h - число
частей, на которые разбивается область интегрирования.
Одна
из формул дает значение интеграла с избытком, другая с недостатком. Какая из
них выдает решение с избытком или с недостатком, зависит от вида
подынтегральной функции.
Формула
трапеций. Эта формула имеет вид:
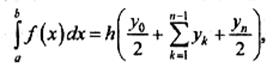
где у0 — значение подынтегральной
функции при х=а, уn — значение подынтегральной функции при х=b, h — шаг
интегрирования.
Формула
парабол (Симпсона). Эта формула имеет
вид:


В
этой формуле ординаты с нечетными индексами умножаются на 4, а с четными — на
2. Предполагается, что n — число
четное.
При
нечетном n формула имеет вид:
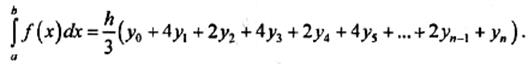
Крайние
ординаты имеют коэффициент, равный 1.
Существует
много других квадратурных формул вычисления интегралов: Котеса, Чебышева,
Гаусса и др.
В системе Matlab вычисление интегралов реализовано численными методами трапеций, парабол (Симпсона)
и Ньютона - Котеса.
Метод трапеций. Метод трапеции реализован в Matlab несколькими функциями, приведенными ниже.
1. Функция cumtrapz(у). Осуществляет вычисление интеграла в случае, когда
значения функции у заданы в виде вектора или матрицы неограниченных размеров.
Откликом этой функции является п интегралов, где п — число
элементов вектора или число элементов в каждом столбце матрицы. Такое
вычисление интеграла называется интегрированием с накоплением.
Пример 1. Пусть функция
у(х) имеет значения, представленные в виде следующего вектора: у=
[1,2,3,4,5,б,7,8,9,10]. Необходимо вычислить 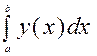
При этом a=1; b=1,2, 3,...,
10.
Функция
вычисления интеграла методом трапеций будет иметь вид:
>> у=[1, 2, 3, 4, 5, 6,
7, 8, 9, 10];
>> cumtrapz (у)
ans =
0
1.5000 4.0000 7.5000
12.0000 17.5000 24.0000
31.5000 40.0000 49.5000
Пример 2. Пусть необходимо вычислить интеграл вида  .
.
Чтобы
вычислить этот интеграл с помощью функции cumtrapz(), следует сначала вычислить
10 ординат подынтегральной функции, представив их в виде вектора.
Программа
вычисления интеграла с накоплением будет иметь вид:
» х=1:1:10;
» y=3*exp(x)+log(x)+l;
» cumtrapz(у)
ans =
1.0e+004 *
0 0.0017
0.0060 0.0174 0.0481
0.1311 0.3564 0.9684
2.6313 7.1510
Существует модификация данной
функции cumtrapz (х, у). Основным
недостатком метода трапеций является большая погрешность результата вычисления
интеграла.
2. Функция trapz(y). Отличие данной функции от функции cumtrapz(y) состоит в
том, что осуществляется простое интегрирование без накопления, то есть trapz(y) возвращает не столько интегралов, насколько шагов
разбивается область интегрирования, а общее значение интеграла.
Пример 3. Вычислить интеграл
вида  с шагом 0,5.
с шагом 0,5.
x=1: 0.5: 10;
y=x.*exp(x) + log(x) + 1;
trapz(y)
ans = 4.0657e+005.
Существует
модификация данной функции trapz (х, у).
Следует иметь в виду, что при
вычислении интеграла с помощью функции trapz (х, у) его значение зависит от
шага интегрирования.
Метод
парабол (Симпсона). Для его
реализации в системе Matlab
используются следующие функции:
quad('fun', a, b),
quad('fun', a, b, tol),
quad('fun', a, b, tol, trace),
dblquad('fun', a, b, c, d),
dblquad('fun', a, b, c, d,
tol).
В
этих функциях приняты обозначения:
Вернуться назад к содержанию
1) 'fun' - подынтегральная
функция, взятая в одинарные кавычки;
2) а, b - пределы интегрирования;
3)
tol - относительная погрешность,
задаваемая пользователем (по умолчанию tol = 10e -3);
4) с,d -
пределы интегрирования по другой переменной (внешней) при вычислении двойного
интеграла;
5) trace — число, отличное от
нуля, по которому система показывает ход вычислительного процесса.
Рассмотрим
перечисленные функции и приведем примеры.
1. Функция quad('fun',
a, b). Функция вычисляет
пределенный интеграл  с погрешностью, не превышающей 10-3.
с погрешностью, не превышающей 10-3.
Пример 4. Подынтегральная функция
имеет вид: f(x) = е х +
х 2 + 2 sin х - 5 .
Подынтегральная функция
имеет вид: f(x) = е х +
х 2 + 2 sin х - 5 .
Необходимо вычислить
интеграл.
Решение:
>> у = ‘ехр(х) + х.^2 +
2*sin(х) – 5’;
>> quad (у, 1, 5)
ans
= 167.5415
Функция может быть
представлена одной строкой:
quad (‘ехр(х) + х.^2 + 2*sin(х) – 5’,
1, 5).
2. Функция dblquad('fun',a,b,c,d).В функции dblquad ('fun', a, b, с, d) приняты следующие обозначения:
'fun' - это функция с двумя
переменными;
а,
b - пределы по внутренней переменной;
с,
d - пределы по внешней переменной.
Пример 5.
Пусть функция двух переменных имеет вид:
z = x2 + y2 - 2 .Необходимо вычислить интеграл 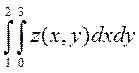
Решение:
>> z='x.^2 + y.^2 - 2';
>> dblquad (z,1,2,0,3)
ans = 10.
Вычисления
кратных интегралов. Наиболее просто
кратный интеграл вычислить путем интегрирования ответа, полученного от
предыдущего значения интеграла.
Пример.
Пусть необходимо вычислить двойной неопределенный интеграл

Решение.
>> syms x;
>> y=x/(1-x^2);
>> int(int(y))
ans = -1/2*log(x-1)*(x-1)+x-1/2*log(x+1)*(x+1)
Вернуться назад к содержанию
Перейти к лабораторной работе 4
Лабораторная
работа №1
Введение в систему научных и инженерных
расчетов Matlab
Целью данной
работы является ознакомление с системой научных и инженерных
расчетов Mat Lab, получение начальных сведений об окне управления,
окне встроенного редактора, ознакомление с простейшими операциями с числами,
векторами и матрицами, элементарными математическими функциями и создание
М-файлов.
Задание на лабораторную работу
1. Осуществить ввод действительного числа 2,15*10-7.
2. Выполнить простую арифметическую операцию 8,3/6*2,7-0,001^2*3,14
3. Осуществить ввод комплексного числа, действительная
часть которого равна 4, а мнимая равна -9.
4. Выполнить простую арифметическую операцию с двумя
комплексными числами, используя одну из дополнительных функций комплексного
аргумента.
5. Вычислить значение одной из элементарных
математических функций (смотри стр. 6 и 7 )
6. Сформировать вектор из 5 любых неотрицательных
элементов.
7. Сформировать матрицу размером 3х4 с 1 по главной
диагонали и нулевыми остальными элементами.
8. В созданной матрице извлечь элемент 2-й строки и
3-столбца
9. Растянуть данную матрицу в один вектор
10.
Создать 2 вектора х и y по 3 элемента каждый и провести операции сложения,
вычитания, транспонирования векторов, и их перемножения
11.
Создать М-файл, реализующий вычисление
следующей функции

Вернуться назад к
содержанию
Лабораторная
работа №2
Графика в Matlab
Целью данной
работы является ознакомление с графической системой Matlab, получение начальных сведений об окне управления,
окне встроенного редактора, ознакомление с функциями построения двумерных,
полярных и трехмерных графиков.
Задание на лабораторную работу
1.
Построить график функции y = (cos (x/π+ π)+sin(x))/2; на промежутке от -3π до +3π с шагом π/50.
Этот
график выполнить зеленым цветом, точки графика в виде звездочек, линия
сплошная.
2.
Добавить к полученному графику координатную сетку, заголовок и названия осей.
3.
Осуществить вывод функции y = cos (x/π+ π) в виде
ступенчатого графика в диапазоне от 0 до 100 с шагом 0.5
4.
Построить график функции y = ex в виде столбчатой диаграммы на отрезке от -3 до 3.
5. Построить 4 графика произвольных функций в одном
графическом окне.
6.
Построить график
функции z = sin х + 2cos у в диапазоне аргументов
[-3; 3] с шагом h = 0.05.
7.
Выполнить
построение каркаса поверхности и самой поверхности. Исходными данными является
матрица (5х5) из случайных чисел, равномерно распределенных в диапазоне от 0 до
1.
Вернуться назад к содержанию
Лабораторная
работа №3
Матричные действия над матрицами. Операции с полиномами.
Целью работы
является ознакомление с матричными
действиями над матрицами в системе Matlab, получение
навыков для выполнения операций с полиномами в системе Matlab.
Задание на
лабораторную работу
1)
Провести операции сложения, вычитания, перемножения произвольных матриц
размером (4х4), умножения матрицы на целое положительное число,
транспонирования матрицы.
2)
Найти обратную матрицу для произвольной матрицы
3)
Используя функцию обращения матрицы и функцию деления матриц решить систему
линейных уравнений:
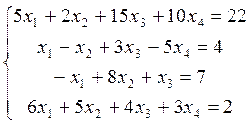
4)
Найти корни полинома Р(х) = 2х6+3х5+4x4+12x3+5x2+6x+5
5)По
заданному вектору корней полинома (R = [2;
4; 8; 16; 32]) найти его коэффициенты.
6)
Вычислить значение полинома из задания 4 при аргументе равном 5.
7)
Вычислить производную от полинома P(x).
Вернуться
назад к содержанию
Лабораторная работа №4.
Алгоритмы и технологии вычисления интегралов
Целью работы
является ознакомление с технологиями
вычисления интегралов в системе Matlab.
Задание на лабораторную работу
1)
Провести интегрирование с накоплением (шаг интегрирования равен 0,5) для
интеграла 
2)
Вычислить значение интеграла (интегрирование с накоплением) от функции
представленной в виде вектора корней полинома:
Р(х) = х5+8x4+31x3+80x2+94x+20
3) Вычислить
с помощью метода трапеции (шаг интегрирования равен 1) значение интеграла

4) Подынтегральная функция
имеет вид:
f(x) = -е х
+ 8х 4 + 3 ctg х + 1.
Вычислить
методом Симпсона значение интеграла от f(x) с точностью 10-5.
Пределы интегрирования [1; 10].
5) Вычислить методом парабол значение двойного
интеграла от функции z = ln(x)+ln(y).
Пределы интегрирования по 1 переменной [1, 5], а по внешней переменной [2; 4].
6) C помощью аналитического метода
найти значение неопределенного интеграла 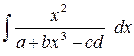
7) C помощью аналитического метода
вычислить значение определенного интеграла
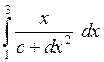
8)
Вычислить интеграл 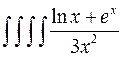
Вернуться назад к
содержанию
Лабораторная работа № 5
Режим программирования в Matlab
Целью работы является ознакомление с применением команд управления
потоками в системе Matlab.
Задание на лабораторную работу:
1) Имеются 3 переменные a, b и i. Переменная b=15,
переменная a=i/2 и переменная i=1. На каждом шаге i увеличивается на 1. Определить число шагов, за
которое, а достигнет большего, чем b значения.
2) Имеются 2 переменные n и m. Переменная n может принимать одно из двух значений
0 (m=n) или 1 (m=n+n/2). Используя оператор переключения
для переменной n, определить значение переменной m в каждом из этих случаев.
3) Дана матрица размером n x m. Произвести суммирование всех
элементов матрицы кроме элементов последнего столбца и последней строки
(используя вложенные циклы).
4) Создать функцию
зависимости y от k и t в виде:
Если k=1, то y=(k*t)/2
Если k=2, то y=0
Создать меню выбора значения
переменной k, которое может принимать значения 1 или 2.
5) Создать файл-функцию
для расчета факториала числа 8.
Вернуться назад к содержанию
Литература
1.
В.П. Дьяконов. MATLAB 6.0/6.1/6.5/6.5 + SP1 +
Simulink 4/5. Обработка сигналов и изображений. М.: СОЛОН-Пресс, 2004. -
592 с.
2.
В.Потемкин. Вычисления в среде MATLAB. Диалог-МИФИ.
2004.
3.
Кривилев А. Основы компьютерной математики с
использованием системы MATLAB. Лекс-Книга, 2005.
4.
В.П.Дьяконов. MATLAB 6/6.1/6.5 + Simulink 4/5. Основы
применения. Полное руководство пользователя . СОЛОН-Пресс, 2004.
5.
Н.Мартынов. Введение в MATLAB 6. Кудиц-образ.
2002.
Вернуться назад к содержанию


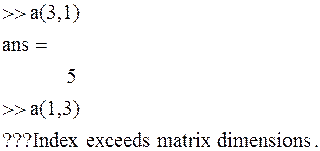









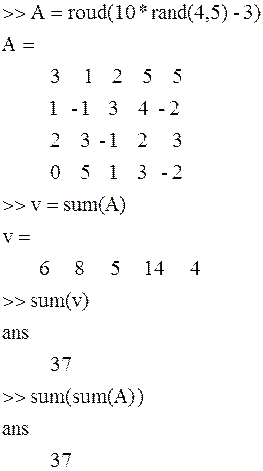























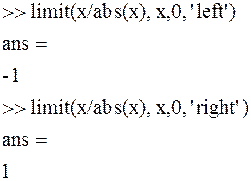
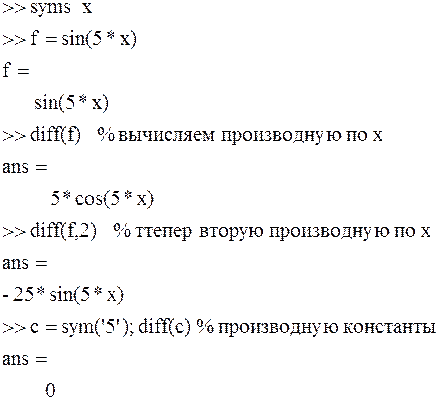
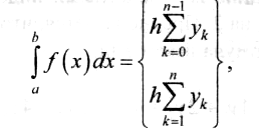
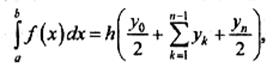
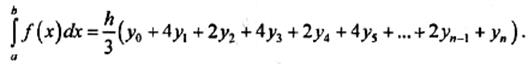
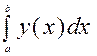
 .
.
 с погрешностью, не превышающей 10-3.
с погрешностью, не превышающей 10-3.