Лабораторная работа № 3

Вычисление границ доверительных интервалов в Excel.

 

Цели и задачи работы.

Цель работы – научиться вычислять интервальные оценки параметров случайной величины: интервальные оценки математического ожидания и дисперсии нормального распределения, интервальная оценка вероятности события.

Задачи работы:

·       уметь исследовать распределение случайной величины .заданной распределение К. Пирсона;

·       уметь исследовать распределение случайной величины заданной распределением Стьюдента (t-распределение);

·       уметь исследовать распределение случайной величины заданной распределением Фишера (F-распределение);

·       иметь понятие интервальной оценки параметра случайной величины;

·       уметь вычислять интервальные оценки математического ожидания нормального распределения;

·       уметь вычислять интервальные оценки дисперсии нормального распределения;

·       уметь вычислять интервальные оценки вероятности события;

·       научиться вычислять величины , ,  ,,  с помощью встроенных функций Excel.

Теоретическая часть.

1.  Некоторые распределения выборочных характеристик.

         Генеральные совокупности часто имеют нормальный закон распределения. В этом случае многие выборочные характеристики, в том числе , выражаются через небольшое  число распределений. В математической статистике, как правило,  используются не плотности этих распределений, а некоторые характеристики, представленные таблицами. Чаще всего в качестве такой характеристики выступает квантиль распределения.

Квантилем уровня   или p-квантилем случайной величины  называется такое число dp, что вероятность   равна заданной величине p.

Из определения следует, что если непрерывная случайная величина имеет плотность распределения p(x), то квантиль dp определяется равенством

                   (1)

         Это означает, что площадь фигуры, ограниченной осью абсцисс, кривой f(x)  и прямой    x=dp, равна величине p. На рис.1,а показан квантиль  , а на рис.1,б – квантиль . Площади заштрихованных фигур равны 0,1 и 0,9 соответственно.

 

 

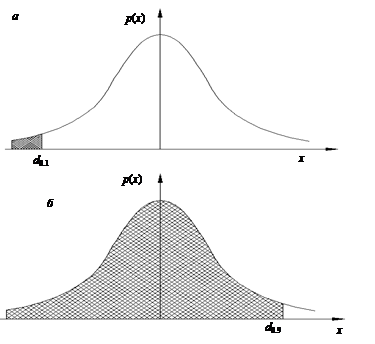
Рис.1  Определение квантилей случайной величины.

 

Рассмотрим несколько распределений, которым подчиняются выборочные характеристики и которые используются для построения интервальных оценок.

Распределение  (распределение К.Пирсона). Пусть N1…Nn – независимые нормально распределенные случайные величины с параметрами (0,1), распределение случайной величины

            (2)

Называется распределением  с n степенями свободы, а сама величина   - случайной величиной с n степенями свободы.

Заметим, что количество степеней свободы n является единственным параметром - распределения и значения неотрицательны, т.е.   .

Определим математическое ожидание величины . По определению (2) имеем

так как ,

Но , , а значит, .

Нетрудно вычислить и дисперсию случайной величины . Так как случайные величины независимы , то

.                 (3)

Плотность распределения случайной величины  равна . Следовательно,

.

Последний интеграл вычисляется методом интегрирования по частям. Далее, так как , то . Таким образом, - распределение с n степенями свободы имеет следующие числовые характеристики:             (4)

Согласно центральной предельной теореме, если случайные величины  независимы, одинаково распределены и имеют конечные дисперсии, то последовательность  асимптотически нормальна. Другими словами, при больших значениях n распределение случайной величины  близко к нормальному распределению с параметрами . Однако при малых значениях n функция плотности случайной величины значительно отличается от кривой Гаусса.

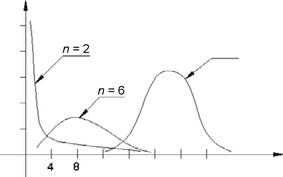
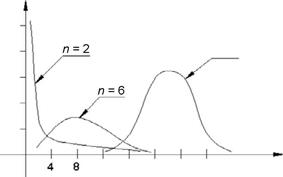
На рис. 2 показаны плотности распределения p(x) случайной величины  при n=2, n=6 и n=20. Видно, что при увеличении n плотность p(x) «приближается» к плотности нормального распределения.

п = 20

12     16    20    24    28

Р(х)
 

 

 

 

 

х
 
 


Рис. 2. Плотность распределения

 

         Обратим внимание на одно замечательное свойство распределения . Строго, говоря это свойство состоит в том, что сумма независимых случайных величин  также распределена по закону   с (n+m) степенями свободы. Объясняется это тем,что случайная величина  представляется в виде суммы (n+m) квадратов случайных величин, независимых и нормально распределенных с параметрами (0,1).

         Распределение Стьюдента  (t-распределение). Пусть N(0,1) – нормально распределенная величина с параметрами  , а  - независимая от N(0,1) случайная величина, подчиняющаяся распределению  с n степенями свободы. Тогда

                                         (5)

называется t-распределением или распределение Стьюдента. Сама случайная величина (5) называется t-величиной с n степенями свободы. Плотность вероятности случайной величины  Tn имеет вид

, где Bn- некоторая константа, удовлетворяющая условию нормирования . При больших значениях n кривая  близка к кривой нормального распределения N(0,1). Поэтому в практических расчетах при n>30 часто считают, что

.

Заметим, что функция плотности симметрична относительно оси ординат.

Распределение Фишера (F-распределение). Пусть  -независимые случайные величины, имеющие - распределение с n и m степенями свободы соответственно. Распределение случайной величины

                               (6)

называется F- распределением или распределением Фишера с n и m  степенями свободы, а сама величина (6) -  величиной. Так как случайные величины, то .

В дальнейшем мы часто будем ссылаться на следующую теорему о распределении выборочных характеристик  , доказанную Р.Фишером.

         Теорема: ( о распределении выборочных характеристик). Если генеральная совокупность X распределена по нормальному закону с параметрами a и σ, то:

а) случайная величина  распределена нормально с параметрами ;

б)  имеет распределение $

в) случайные величины  и  независимы.

         Мы не будем полностью доказывать эту теорему, а ограничимся доказательством утверждения а). Очевидно, что  есть линейная комбинация

 независимых, нормально распределенных случайных величин. Как отмечалось в курсе теории вероятностей, в этом случае случайная величина  распределена нормально.

Легко получить, что

,

.

Тем самым первое утверждение теоремы доказано.

         Как следует из в), используя случайные величины  и , можно составить случайную величину .

Действительно, пронормировав , получим .

Так как  и

.

Итак, мы получим

Следствие. Если условия теоремы о распределении выборочных характеристик выполнены, то случайная величина

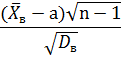
имеет распределение Стьюдента с  степенями свободы. Напомним, что исправленная дисперсия  определяется как

.

Тогда получаем новое

Следствие. Если условия теоремы о распределении выборочных характеристик выполнены, то случайная величина

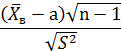
имеет распределение с (n-1) степенями свободы.

 

2.    Понятие интервальной оценки параметра случайной величины.

         Вычисляя на основе результатов наблюдений точечную оценку  неизвестного параметра , мы понимаем, что величина является (в силу своей случайности) лишь приближенным значением параметра . При большом числе наблюдений точность приближения бывает достаточной для практических выводов в силу несмещенности, состоятельности и эффективности «хороших» оценок. Для выборок малого объема точечные оценки могут значительно отличаться от оцениваемого параметра и вопрос о точечности получаемых оценок становится очень важным. В математической статистике он решается введением интервальных оценок.

         Интервальной оценкой для параметра  называется такой интервал  со случайными границами, что

.

Вероятность γ называется надежностью интервальной оценки или доверительной вероятностью, случайные величины  - доверительными границами, а сам интервал  иногда называют доверительным интервалом. Центром этого интервала является значение точечной оценки .

         Надежность γ принято выбирать равной 0,95 . 0,99. Тогда событие, состоящее в том, что интервал покроет параметр , будет практически достоверным.

Общая теория построения интервальных оценок заключается в определении случайной величины, зависящей от оцениваемого параметра. Зная распределение этой случайной величины, находят соответствующие доверительные границы и сам доверительный интервал с требуемой точностью. Посмотрим, как эта идея реализует для различных параметров.

 

3.    Интервальные оценки математического ожидания нормального распределения.

Пусть генеральная совокупность X распределена по нормальному закону , причем параметр σ известен, а параметр a  требует оценить с надежностью γ. По теореме о распределении выборочных характеристик случайная величина   распределена по закону N(0,1) . На рис. 3 изображен график функции плотности этой случайной величины, т.е. кривая  . Выберем число , т.е.

.

 

 

 

 

 

 

 

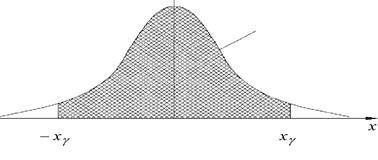
Рис. 3.

Построение доверительных интервалов

 

         Это значение легко находится с использованием интегральной функции Лапласа .

Действительно,

        (9)

Значение , удовлетворяющие нелинейному уравнению

                                         (10)

находится по таблице нормированной функции Лапласа (Приложение 1).

         Так как , то события  и  ‘эквивалентны, а значит, их вероятности равны:

.            (11)

Таким образом, для параметра a мы построили доверительный интервал (интервальную оценку), левая граница которого - , правая - , а точность – . Центр этого интервала находится в точке с координатой  , а длина интервала . Если объем выборки неограниченно возрастает, то интервал стягивается в одну точку , которая является состоятельной и несмещенной оценкой для параметра a.

         Пример 1: По выборке объема n=9 найдено среднее значение . Считая, что генеральная совокупность распределена по нормальному закону с , определить интервальную оценку для математического ожидания с надежностью .

Решение. Используя таблицу Приложения 1, находим, что

При . Тогда  и доверительный интервал (11) имеет границы . Таким образом, с вероятностью 0,95 можно быть уверенным в том, что интервал

                  (12)

накроет параметр a или, другими словами, с вероятностью 0,95 значение  дает значение параметра a с точностью .

Заметим, что эта трактовка неверна, если вместо случайной величины  использовать вычисленное по конкретной выборке значение  Тогда границы интервала (0,19;2,81) будут не случайными и возможны два случая:

·       Точка а лежит внутри этого интервала, тогда ;

·       Точка а не лежит внутри (0,19;2,81), тогда ;

 

Поэтому только для интервала (12) со случайными границами можно утверждать, что

Определим теперь интервальную оценку для неизвестной генеральной средней  нормально распределенной генеральной совокупности X в том случае, когда генеральная дисперсия  неизвестна, т.е. построим доверительный интервал для параметра а, если параметр  σ неизвестен.

В отличие от предыдущего случая, вместо случайной величины , распределенной по закону N(0,1), рассмотрим случайную величину  , которая согласно следствию из теоремы 1 распределена по закону Стьюдента . При заданном значении γ, пользуясь таблицей Приложения  3 (Значения чисел q в зависимости от объема выборки n и надежности γ для определения доверительного интервала среднего квадратического отклонения ), вычислим значение t(γ,n) из условия

,                   (13)

где γ – надежность интервальной оценки. Заметим, что в таблице Приложения 3 n означает не число степеней свободы, а объем выборки. Число степеней будет n-1.

         Замена случайной величины  на случайную величину  вызвана тем, что закон распределения последней случайной величины известен и в ее запись не входит неизвестный в данном случае параметр σ. Из условия (13) получаем

.

Таким образом, интервальная оценка надежности γ для неизвестной генеральной средней a имеет границы

.

Выразим границы интервала через исправленную дисперсию . Так как , то . Поэтому

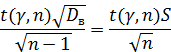
Значит, границы доверительного интервала можно записать как

,                (14)

а точность интервальной оценки определить соотношением

                   (15)

         Как и в предыдущем случае, центр интервала находится в точке  , но длина интервала  является случайной величиной, принимающей тем меньшие значения, чем больше значение n. Это объясняется тем, что наличие большей информации  о генеральной совокупности X позволяет сузить интервал.

         Пример 2: По выборке объема n=9 из нормально распределенной генеральной совокупности найдены значения  и s=2. Построить интервальную оценку для математического ожидания с надежностью .

Решение. Пользуясь таблицей Приложения 3, находим величину . Тогда точность δ определяется соотношением (15): , а интервальная оценка имеет границы , которые зависят от двух случайных величин:  и S . Подставляя вместо S ее вычисленное значение  S=2, получаем интервал .

Сравнивая эту оценку с интервальной оценкой примера 1 (см.(12)), видим, что замена неизвестной величины σ вычисляемой величиной S приводит к уменьшению точности интервальной оценки и увеличению длины доверительного интервала. Подставив вместо случайной величины  ее конкретное значение , получаем конкретное значение границ (0;3).

 

a.    Интервальные оценки дисперсии нормального распределения.

         Как и при построении интервальных оценок для математического ожидания, в данном случае также необходимо определить случайную величину, распределение которой было известно и включало оцениваемый параметр σ. В соответствии с теоремой 1 такой отправной точкой для построения доверительного интервала может быть случайная величина , распределенная по закону  с (n-1) степенями свободы. Заметим, что доверительные интервалы, построенные для параметра a, вообще говоря, можно было выбрать несимметричными относительно  и это не противоречило бы определению интервальной оценки. Но такой выбор интервала, когда в его середине лежит состоятельная и несовмещенная оценка параметра, являлся предпочтительным. В данном случае целесообразно выбрать два предела  так, что

,

где , γ-надежность интервальной оценки.

         Следовательно, –квантиль -распределения уровня .  - уровня .

Тогда имеет место равенство , а интервал

               (16)

является интервальной оценкой  надежности γ.

Так как , то  и интервал

            ,                    (17)

является интервальной оценкой для  надежности γ.

         Заметим, что границы интервалов (16), (17) являются случайными величинами и с вероятностью γ можно утверждать, что интервалы (16), (17) накроют неизвестную дисперсию .

         Пример 3: По выборке объема n=20 из нормально распределенной генеральной совокупности вычислено значение дисперсии выборки . Построить интервальную оценку для параметра  надежности γ=0,96.

Решение: Значения   находим из условий:

.

Эти условия означают, что  есть  квантиль -распределения с 19 степенями свободы уровня 0,02, а  – квантиль уровня 0,98. По таблице Приложения 3 квантилей -распределения находим

;

Тогда интервальная оценка (16) примет вид

.

Подставляя вычисленное значение случайной величины , получаем

.

 

b.    Интервальная оценка вероятности события.

Выше было показано, что «хорошей» точечной оценкой вероятности p события является частность  (см.(17)), где n – общее число независимых испытаний, в каждом из которых событие А может произойти с вероятностью p, а m – число испытаний , в которых произошло событие A.

         Зададим надежностью интервальной оценки  γ и найдем числа такие, чтобы выполнялось соотношение

.

         Интервальную оценку построим для двух случаев: когда число испытаний n сравнительно велико  и для малого числа испытаний.

Интервальная оценка вероятности при большом числе испытаний.

Если , то распределение случайной величины  можно аппроксимировать нормальным распределением  . Следовательно, при этих же условиях распределение величины   близко к нормальному с нулевым математическим ожидание и единичной дисперсией, т.е.

. (18)

По аналогии с (8) найдем такое число , для которого справедливо равенство

. (19)

         Это число является корнем уравнения

,

где - функция Лапласа, и корень может быть найден с помощью табл. П1.

         Неравенство, стоящее в скобках выражения (19), разрешим относительно p. Для этого неравенство перепишем в виде эквивалентного неравенства . Возведем в квадрат, в результате получим . Далее возведя в квадрат  и перенеся все члены влево, получим

.

Корни p1 и p2 квадратного трехчлена, состоящего в правой части неравенства, определяются выражениями

,                                                   (20)

 

 .                                                    (21)

 

Корни этого уравнения и являются границами интервальной оценки (18)

.                            (22)

Если , то для вычисления p1и p2 можно использовать приближенные формулы:

;   .          (23)

 

Видно, что границы интервала (18) являются случайными величинами и конкретные значения границ получаются в результате подстановки наблюдаемого значения случайной величины .

 

Пример 4: Событие A в серии из n=100 испытаний произошло m=78 раз. Построить интервальную оценку для вероятности p события с надежностью γ=0,9.

Решение. Значение точечной оценки вероятности p равно . По табл. П1 определяем  и вычисляем по формулам (20), (21) значения p1 и p2  при : p1=0,705, p2=0,848. Таким образом, получили реализацию достоверного интервала (0,705;0,848) для вероятности p события A.

Интервальная оценка вероятности при малом числе испытаний. При малом числе испытаний n  предположение о приближенном распределении случайной величины m необходимо использовать формулу Бернулли:

,  .

         Можно показать, что граничные точки интервальной оценки (18) являются решениями следующих нелинейных уравнений:

 

 ;                          (24)

 

,                            (25)

 

где γ – надежность интервальной оценки. Вновь заметим, что решения   этих уравнений являются случайными величинами и только при подстановке конкретного значения m  (количество испытаний, в которых появилось событие A) будут получены конкретные значения граничных точек интервальной оценки (18).

         Корни уравнений (24), (25) могут быть найдены одним из известных численных методов решения нелинейных уравнений. Кроме этого, существуют специальные таблицы для нахождения , удовлетворяющих уравнениям (24), (25) по заданным n, m-n, γ. Фрагмент этих таблиц представлении в приложении (табл.П4).

         Пример 5: В пяти испытаниях событие A произошло три раза. Построить интервальную оценку для вероятности p события A с надежностью, γ=0,95.

         Решение: Из условий примера , имеем  n=5, m=3, γ=0,95. По таб.П4 находим , , а интервальная оценка определяется как (0,147;0,947).

Сравнивая интервальные оценки примеров 4, 5, видим, что длина доверительного интервала для примера 5 (равна 0,8) существенно больше длины доверительного интервала примера 4 (0,143). Это является следствие разного объема выборок (n=5 и n=100) и различных дисперсий случайной величины  .

 

4.    Вычисление границ доверительных интервалов в Excel.

         Границы доверительных интервалов зависят от некоторой величины, которая зависит от распределения точечной оценки и доверительной вероятности. Эта величина находится по специальным таблицам. Поэтому часто возникает необходимость интерполяции или экстраполяции табличных данных и, следовательно, требуются дополнительные вычисления. В табличном процессоре Excel определены функции, позволяющие в интервальные оценки для различных числовых характеристик случайной величины.

 

Вычисление величины , входящей в доверительный интервал (11):

,                                              (26)

 

Величина  является корнем нелинейного уравнения (10) и вычисляется с помощью функции НОРМСТОБР:

,

Где γ – надежность интервальной оценки (26).

         Вычисление величины  осуществляется с помощью функции ДОВЕРИТ:

,

где , σ – известное среднеквадратическое отклонение, n – объем выборки. Тогда интервальную оценку (26) можно записать в виде

 .

         Вычисление величины , входящих в доверительный интервал

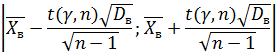
осуществляют с использованием функции СТЬЮДРАСПОБР,  обращение к которой имеет вид:

,

где , n – число степеней свободы.

 

         Вычисление величин  , , входящих в доверительный интервал (17) для дисперсии :

,

где - исправленная дисперсия. Используется функция ХИ2ОБР:

;

.

где  , γ – надежность интервальной оценки.

 

Пример решения задач в Excel.

Запишите условие Примера 1 в среде Excel. Оформите исходные данные примера в виде таблицы. Значения n, xв, σ, γ, Ф(x), xγ.δ занесите в ячейки 1:4,2:4,3:4,4:4,5:4,6:4,7:4.

         В ячейке5:4 вычислите значение интегральной Функции Лапласса.

В ячейке 6:4 вычислите значение xγ с помощью встроенной функции НОРМСТОБР

 

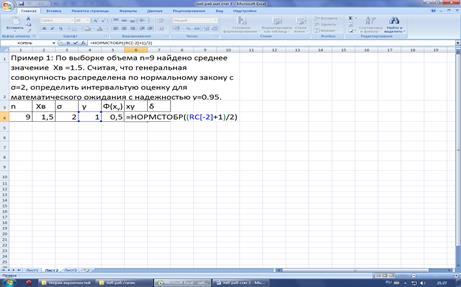
В ячейке 7:4 вычислите точность δ с помощью встроенной функции ДОВЕРИТ

 

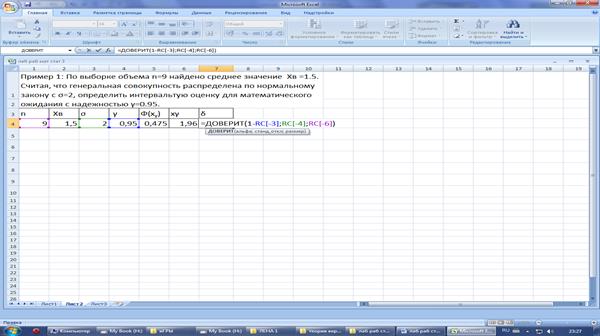
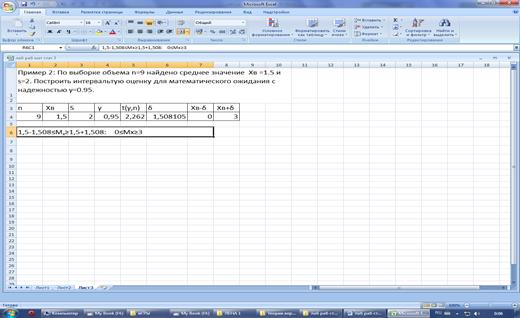
Запишите условие Примера 2 в среде Excel. Оформите исходные данные примера в виде таблицы. Значения n, xв, s, γ, t(γ, n), δ занесите в ячейки 1:4,2:4,3:4,4:4,5:4,6:4,7:4.

         Под таблицей запишите результат интервальной оценки математического ожидания случайной велисчины.

         В ячейке 5:4 вычислите значение величины t(γ, n) с помощью встроенной функции  СТЬЮДРАСПОБР.

 

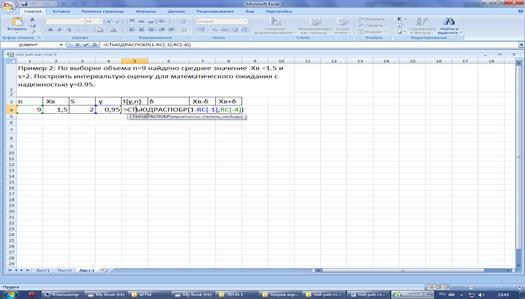
         В ячейке 6:4 вычислите значение  точности δ

 

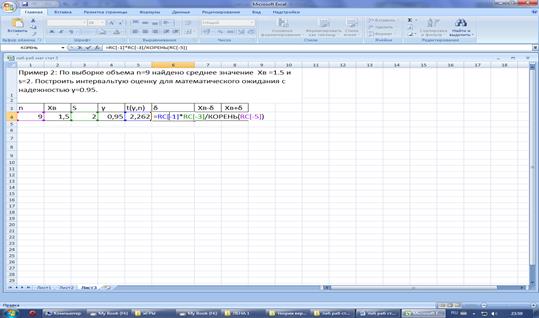
         Под таблицей запишите результат интервальной оценки математического ожидания случайной велисчины.

               

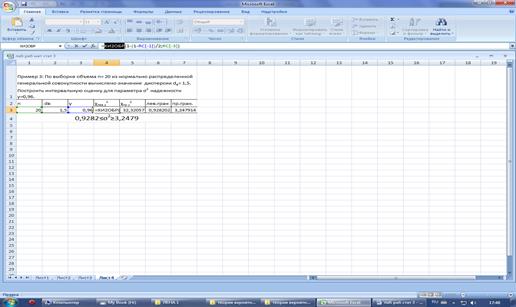
Запишите условие Примера 3 в среде Excel. Оформите исходные данные примера в виде таблицы. Значения n, dв,  γ, χлев.γ2, χпр.γ2 занесите в ячейки 1:4,2:4,3:4,4:4,5:4.

С помощью функции ХИ2ОБР в ячейках 4:4;4:5 вычислите значения χлев.γ2  и  χпр.γ2. В ячейках  6:4;7:4 вычислите значения левой и правой границ интервальной оценки дисперсии нормального распределения σ2.

 

 

Варианты заданий для самостоятельного решения:

1.    Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания a нормально распределенного признака X генеральной совокупности, если генеральное среднее квадратическое отклонение σ, выборочная средняя  и объем выборки n .

№ варианта

Надежность γ

Генеральное среднее квадратическое отклонение σ

Выборочная средняя

Объем выборки n

1

0,95

5

14

25

2

0,95

8

12

25

3

0,95

5

14

20

4

0,95

8

12

25

5

0,97

6

15

25

6

0,97

7

13

20

7

0,97

6

12

30

8

0,97

8

11

30

9

0,99

4

10,4

16

10

0,99

5

10,2

25

11

0,99

4

16,2

20

12

0,99

7

15

16

13

0,95

40

2000

5

14

0,95

10

100

5

15

0,95

30

2000

10

 

2.    По выборке объема n из нормально распределенной генеральной совокупности найдены значения  и s. Построить интервальную оценку для математического ожидания с надежностью .

 

№ варианта

Надежность γ

«исправленное» среднее квадратическое отклонение s

Выборочная средняя

Объем выборки n

1

0,95

5

1,4

9

2

0,95

8

1,2

10

3

0,95

5

1,4

9

4

0,99

2

12

15

5

0,95

6

1,5

8

6

0,95

7

1,8

10

7

0,95

6

10

9

8

0,99

2

4,8

9

9

0,99

4

10,4

10

10

0,99

5

10,2

15

11

0,99

4

16,2

10

12

0,99

7

15

16

13

0,95

40

2000

5

14

0,95

10

100

5

15

0,95

30

2000

10

 

3.    По выборке объема n из нормально распределенной генеральной совокупности вычислено значение дисперсии выборки . Построить интервальную оценку для параметра  надежности γ.

№ варианта

Надежность γ

Дисперсия выборки

Объем выборки n

1

0,95

2,5

9

2

0,95

1,8

10

3

0,95

5,7

30

4

0,99

2,9

15

5

0,95

6,6

8

6

0,95

7,1

10

7

0,95

6

9

8

0,99

2,7

30

9

0,99

4,2

10

10

0,99

5,3

15

11

0,99

4,4

10

12

0,99

7,2

16

13

0,95

4,8

20

14

0,95

1,7

5

15

0,95

3,0

10

 

Контрольные вопросы для самопроверки .

1.    Квантилем случайной величины  называется?

2.    Запишите  распределение К.Пирсона.

3.    Чему равны математическое ожидание и дисперсия распределения К Пирсона?

4.    Запишите  распределение Стьюдента.

5.    Запишите распределение Фишера.

6.    Чему равна исправленная дисперсия?

7.    Чему равны интервальные оценки математического ожидания нормального распределения случайной величины?

8.    Чему равны границы интервальной оценки дисперсии случайной нормального распределения?

9.    С помощью какой статистической функции Excel можно вычислить величину  ?

10.                С помощью какой статистической функции Excel можно вычислить величину  ?

11.                С помощью какой статистической функции Excel можно вычислить величину  ?

12.                С помощью какой статистической функции Excel можно вычислить величины ,   ?