ЛЕКЦИЯ 9. ЭЛЕКТРОННЫЙ ГАЗ

9.1. Бозе–газ при низких температурах. Бозе–конденсация

9.2. Магнетизм электронного газа. Слабые и сильные поля

9.1. Бозе–газ при низких температурах. Бозе–конденсация

Отметим, что при низких температурах свойства Бозе-газа существенно отличается от свойств Ферми-газа. Это, по-существу, очевидно из того, что у Бозе-газа состоянием наименьшей энергии, в котором газ находится при абсолютном нуле температуры, должно быть состояние с Е=0 (все частицы в квантовом состоянии ε=0), тогда так ферми-газ при Т=0 обладает отличной от нуля энергией.

Если при заданной плотности понижать температуру, то химический потенциал газа μ, определяемый уравнением

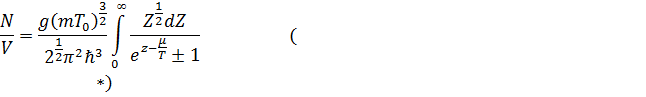
(с нижним знаком), будет увеличиваться, т.е. будучи отрицательным, уменьшается по абсолютной величине и достигнет значения μ = 0 при температуре, определяемой выражением

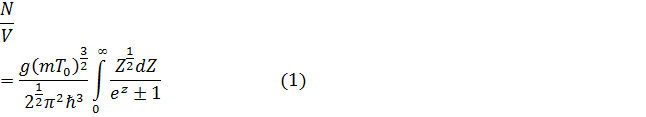
отсюда,

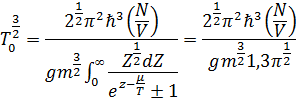
или (2) (здесь интеграл равен )

При Т<Т₀ уравнение (*) не имеет отрицательных решений, хотя химический потенциал в статистике Бозе должен быть отрицательным при всех температурах.

Это кажущееся противоречие связано с тем, что в данных условиях не законен квазиклассический переход от суммирования к интегрированию в формуле (*).

Действительно, при этом переходе первый член суммы (с ε_k = 0) умножается на , т.е. выпадает из суммы. Между тем при понижении температуры частицы должны скапливаться именно в этом состоянии с наименьшей энергией, пока при Т=0 туда не попадут все. Математически это обстоятельство проявляется в том, что в сумме (**)

При переходе к пределу µ→0 сумма всех членов ряда, за исключением первого, стремится к конечному пределу, определяющему интеграл (*), а первый член (с ε_k =0) стремится к бесконечности.

Теперь, если устремим µ не к нулю, а к некоторому малому конечному значению, можно, следовательно, придать указанному первому члену суммы требуемое конечное значение.

Поэтому, в действительности при Т < Т₀ частицы с энергией ε > 0 распределяются по формуле

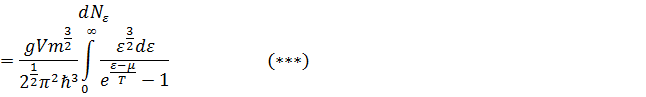
с µ=0 т.е. (3)

Полное число частиц с энергиями ε > 0 будет, следовательно,

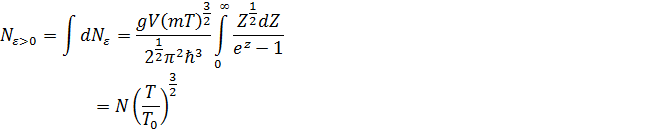
Остальные частицы находятся в низшем энергетическом состоянии, т.е. имеют энергию ε = 0. Число таких частиц будет равно:

(4)

Энергия газа при Т < Т₀ определяется теми частицами, которые имеют ε > 0: Тогда, полагая в выражении для E:

µ=0, имеем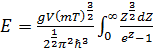

Этот интеграл сводится к и мы получаем

(5)

Теплоемкость такого газа будет равна т.е. пропорциональна (6)

Для энтропии получаем выражение (7)

Свободная энергия будет (8)

Для давления имеем (9)

Таким образом, мы видим, что при давление пропорционально и не зависит от объема. Это и естественно, так как частицы, находящиеся в состоянии с ε = 0, не обладая импульсом, не дают никакого вклада в давление.

В точке T=T₀ все перечисленные термодинамические величины непрерывны. Но, можно показать, что производная от теплоемкости по температуре испытывает в этой точке скачок.

Кривая самой теплоемкости как функция от T имеет в этой точке излом, причем в этой точке теплоемкость максимальна и равна 1.28N.

9.2. Магнетизм электронного газа. Слабые и сильные поля

Известно, что намагниченность электронного газа в слабых полях складывается из двух независимых частей; из парамагнитной намагниченности, которая связана с собственным (спиновым) магнитным моментом электронов (парамагнетизм Паули, 1927г.) и из диамагнитной намагниченности, связанной с квантованием орбитального движения электронов в магнитном поле (диамагнетизм Ландау, 1930г.). Нам необходимо вычислить соответствующие магнитные восприимчивости с учетом, что газ вырожденный, т.е. . Условие слабости магнитного поля означает, что должно быть , где - магнетон Бора.

Для вырожденного газа термодинамические вычисления удобно производить в переменных T, V, μ. Поэтому магнитный момент будем вычислять по формуле (1)

Определим сначала парамагнитную часть восприимчивости. Дополнительная спиновая энергия электрона в магнитном поле равна , где знаки отвечают двум значениям проекции спина в направлении поля. Статистическое распределение электронов в магнитном поле отличается от распределения в отсутствии поля заменой энергии на . Но так как входит в распределение в комбинации с химическим потенциалом, то эта замена эквивалентна замене μ на . Следовательно, термодинамический потенциал Ω электронного газа в магнитном поле можно представить в виде

(2)

где – термодинамический потенциал в отсутствии поля. Здесь два члена отвечают совокупностям электронов с различными проекциями спина, а множители уменьшение вдвое числа квантовых состояний электрона при фиксированном значении проекции его спина.

Произведем в (2) разложение по степеням и получим

(3)

Тогда магнитный момент .

Но , так что парамагнитная восприимчивость, отнесенная к единице объема, будет равна:

(4)

Считая газ полностью вырожденным (при ), имеем из формулы для , что или , и дифференцируя это выражение по μ, получим

(5)

(Здесь использовано соотношение или )

Рассмотрим теперь диамагнитную восприимчивость. Уровни энергии орбитального движения электрона в магнитном поле даются выражением:

, (6)

где n = 0, 1, 2, … . - проекция импульса в направлении поля, которая пробегает непрерывный ряд значений от -∞ до +∞. Число состояний в интервале при каждом заданном значении n есть

, (7)

где множитель 2 учитывает два направления спина. Тогда выражение для потенциала Ω принимает вид

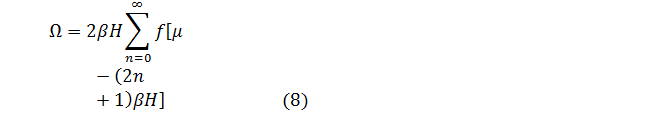
Сумму (8) можно вычислить с требуемой точностью с помощью формулы

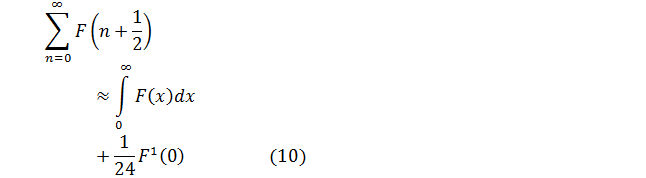
Условие применимости этой формулы состоит в малости относительного изменения функции F на одном шаге . В применении к функции (9) оно сводится к требованию .

Применив (10) к сумме (8), получаем

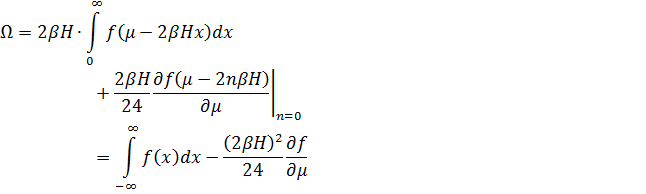
Первый член не содержит H, т.е. представляет собой потенциал в отсутствие поля. Следовательно,

(11)

Тогда магнитная восприимчивость будет равна

(12)