Тема лекции: Определенный интеграл.

План лекции:

1. Определенный интеграл Римана и задачи, приводящие к нему.

2.Основные свойства. Формула Ньютона-Лейбница.

3. Интегрирование по частям и замена переменной в определенном интеграле.

1. Задача о площади  криволинейной трапеции:

Найти площадь фигуры, ограниченную линиями:  на отрезке ,  – ось . Найти площадь . Особенность заключается в том, что верхняя линия в криволинейной трапеции задается функцией. Идея метода – разбить отрезок  на определенные маленькие отрезки и считать площади каждого прямоугольника.

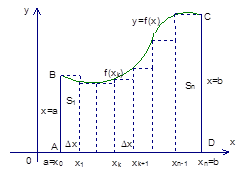
Разобъем отрезок  на  равных частей. Отрезок  разбивается на  равных частей точками  . Величина  . Важно отметить особенности построения.

Если , независимо от того, разобьем мы отрезок на 100, 200 или больше частей. Зафиксируем  и приближенно найдем площадь искомой криволинейной трапеции.

Площадь искомой криволинейной трапеции заменим ступенчатой линией. Значение функции на отрезке [] мы заменим значением функции в левом конце . Таким образом, мы имеем прямоугольники. У них одинаковые основания. А высота – значения функции в левом конце. Площадь первого прямоугольника . Площадь второго прямоугольника . И так далее. . Таким образом, мы разбили площадь на отдельные прямоугольники, сосчитали площадь каждого прямоугольника и суммируем эти площади, получаем:

Итак, при фиксированном  примерное значение функции мы имеем. Но это примерное. Как получить точное?

Устремим . Тогда ступенчатая ломаная будет стремиться занять положение функции . И сумма  будет стремиться к искомой площади. Более точно: .

Пусть функция задана на сегменте , . Обозначим символом разбиение сегмента при помощи некоторых не совпадающих друг с другом точек на частичных сегментов , , …. Точки будем называть точками разбиения . Пусть- произвольная точка частичного сегмента , а - разность которую мы в дальнейшем будем называть длиной частичного сегмента .

Определение 1. Число , где

,

называется интегральной суммой функции , соответствующей данному разбиению сегмента и данному выбору промежуточных точек на частичных сегментах . В дальнейшем через мы будем обозначать длину максимального частичного сегмента разбиения , т.е..

Геометрический смысл интегральной суммы : интегральная сумма представляет собой площадь ступенчатой фигуры, заштрихованной на рис.

Определение 2. Число называется пределом интегральных сумм при , если для любого положительного числа можно указать такое положительное число , что для любого разбиения сегмента , максимальная длина частичных сегментов которого меньше , независимо от выбора точек на сегментах выполняется неравенство

.

Для обозначения предела интегральных сумм употребляется символика .

Определение 3. Функция называется интегрируемой на сегменте , если существует конечный предел интегральных сумм этой функции при . Указанный предел называется определенным интегралом от функции по сегменту и обозначается следующим образом : .

2. Рассмотрим следующие свойства определенного интеграла:

. Мы будем считать, что

. Мы будем считать, что при

. Пусть функции и интегрируемы на сегменте . Тогда функции , и также интегрируемы на этом сегменте, причем

.

. Если функция интегрируема на сегменте , то функция интегрируема на этом сегменте, причем

. Пусть функция интегрируема на сегменте . Тогда эта функция интегрируема на любом сегменте , содержащемся в сегменте .

Пусть функция интегрируема на сегментах и . Тогда эта функция интегрируема на сегменте , причем

Мы доказали, что любые две первообразные данной функции отличаются на постоянную. Поэтому можно утверждать, что любая первообразная непрерывной на сегменте функции имеет вид , где - некоторая постоянная.

Полагая в последней формуле сначала , а затем и используя свойство определенных интегралов, найдем , .

Из этих равенств вытекает соотношение (1)

называемое основной формулой интегрального исчисления.

Итак, для вычисления определенного интеграла от непрерывной функции нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.

Отметим, что основная формула интегрального исчисления открывает широкие возможности для вычисления определенных интегралов, поскольку задача вычисления определенного интеграла сводится к задаче разыскания первообразной функции. Методы разыскания первообразных были достаточно полно разработаны нами.

Формулу (1) иногда записывают в иной форме. Именно, разность обозначают символом . Тогда .

Примеры. 1) ,

2) ,

3) ,

4) ,

5) ,

6) .

3. Пусть выполнены следующие условия:

1) функция непрерывна на сегменте ;

2) сегмент является множеством значений некоторой функции , определенной на сегменте и имеющей на этом сегменте непрерывную производную;

3) , .

При этих условиях справедлива формула .

Примеры. 1) Рассмотрим интеграл . Положим . Т.к. при , при , то .

2) Рассмотрим интеграл . Пусть . Тогда при , при . Поэтому .

Формула интегрирования по частям. Пусть функции и имеют непрерывные произвольные на сегменте . Тогда имеет место следующая формула интегрирования по частям для определенных интегралов:

. Примеры.

1) ,

2) .