Лекция 8. Ряды Фурье для четных, нечетных и - периодических

функций.

План:

1. Ряды Фурье для четных и нечетных функций.

2. Ряды Фурье для функций периода .

3. Ряды Фурье для функций, заданных на конечном отрезке.

I.Отметим некоторые известные свойства четных и нечетных функций.

Если функции и одновременно обе четные или обе нечетные, то их произведение является четной функцией.

Если одна из функций или четная, а другая нечетная, то их произведение является нечетной функцией.

Если - нечетная на функция, то .

Если - четная на функция, то .

Учитывая эти свойства, разложение в ряд Фурье четной или нечетной функции упрощается.

Пусть функция четная и удовлетворяет теореме Дирихле. Тогда функции - четные, а функции - нечетные при любых . Поэтому

, , .

Ряд Фурье для четной функции имеет вид:

.

Пусть функция нечетная и удовлетворяет теореме Дирихле. Тогда функции - нечетные, а функции - четные при любых . Поэтому

, ,

Ряд Фурье для нечетной функции имеет вид:

.

Пример: Разложить в ряд Фурье функцию , с периодом . Данная функция четная, поэтому , , . Данный интеграл вычислим методом интегрирования по частям:

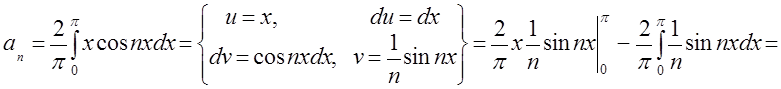
Заметим, что

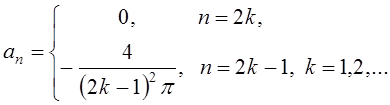
Получим ряд Фурье:

.

II. Пусть функция имеет период , где - любое число. Сделаем замену переменной: , тогда функция имеет период . Действительно, . Разложим функцию в ряд Фурье, считая что она удовлетворяет теореме Дирихле. Получим

, где , , .

Возвратимся к прежней переменной: , , меняется от до , если меняется от до . Ряд Фурье имеет вид:

,

где , , .

Если функция - четная с периодом , то , , . Ряд Фурье для четной функции имеет вид:

.

Если функция - нечетная с периодом , то , , . Ряд Фурье для нечетной функции имеет вид:

.

Пример: Разложить в ряд Фурье функцию , при с периодом .

.

.

.

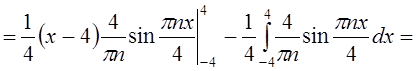
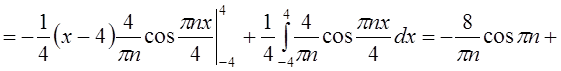
Получаем ряд Фурье:

.

III. Если функция задана на всей числовой оси и непериодическая, то ее нельзя разложить в ряд Фурье, так как сумма тригонометрического ряда является периодической функцией.

Рассмотрим непериодическую непрерывную функцию на промежутке и построим ряд Фурье, который имел бы ее своей суммой в этом интервале. Для этого рассмотрим вспомогательную функцию с периодом , такую что при . Разложив в ряд Фурье функцию , мы получим тем самым разложение на .

Если функция задана только в промежутке , то для разложения ее в ряд Фурье на этом промежутке, нужно сначала продолжить ее каким-то образом на промежуток , а затем продолжить периодически с периодом на всю числовую ось. Чаще всего на промежуток функцию продолжают четным или нечетным образом.

Пример: Разложить в ряд Фурье функцию , заданную на по синусам.

Продолжим данную функцию в интервал нечетным образом, а затем продолжим периодически с периодом на всю числовую ось. Тогда

, ,

.

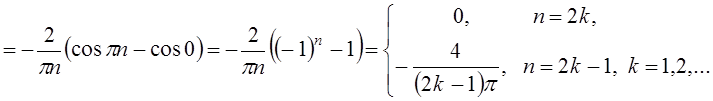
Получаем ряд Фурье:

.