Лекция 7. Тригонометрический ряд Фурье. Сходимость в точке.

Интеграл Дирихле.

План:

1. Тригонометрический ряд Фурье.

2. Интеграл Дирихле.

3. Сходимость ряда Фурье в точке. Признак Дини.

I.Рассмотрим функцию , определенную на промежутке и периодически продолженную . Положим также, что абсолютно интегрируема по Риману. Рассмотрим основную тригонометрическую систему . Напишем некоторый тригонометрический ряд по основной тригонометрической системе

. (1)

Если ряд (1) равномерно сходится на промежутке , то его суммой является непрерывная функция . Из теории рядов знаем, что

. (2)

(2) может иметь место и без требования равномерной сходимости ряда (1). (2) дает возможность заменить функцию с любой заданной точностью частичных сумм тригонометрического ряда. Возникает вопрос, когда же ряд (1) даст нам заданную функцию . Мы уже отмечали, что функция является периодической периода . .

Пусть имеет место следующее равенство

(3)

и ряд справа сходится равномерно. Чему же равны при этом коэффициенты . Интегрируем равенство (3) в промежутке , т.к. функция равномерно сходится.

. (4)

Умножим равенство (3) на и проинтегрируем. Получим

.

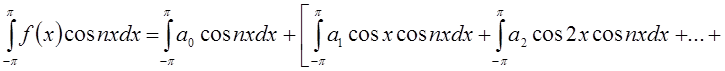
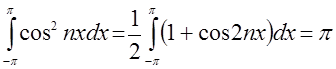
. (5)

Умножая (3) на , и интегрируя в промежутке , получим

. (6)

В итоге получим:

, где ,

, .

Определение. Тригонометрическим рядом Фурье функции называется ряд вида , а числа, определяемые равенствами (4)-(6) называются коэффициентами Фурье.

Равенство (3) при этом называется разложением функции в ряд Фурье.

II. Рассмотрим -ую частичную сумму ряда Фурье для периодической функции с периодом :

, (7) где , . Подставляя эти выражения в формулу (7), получим

, или, подводя и под знак интеграла (что возможно, так как и не зависят от переменной интегрирования и следовательно, могут рассматриваться как постоянные), получим

.

Теперь вынося за скобки и заменяя сумму интегралов интегралом от суммы, получим

, или

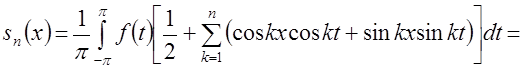
. (8)

Преобразуем выражение, стоящее в квадратных скобках. Пусть

,

тогда

, или

,

.

Но

.

.

Следовательно, .

Таким образом (8) можно переписать так:

.

Так как подынтегральная функция является периодической (с периодом ), то интеграл сохраняет свое значение на любом отрезке интегрирования длины . Поэтому мы можем написать:

.

Введем новую переменную , положив , . Тогда мы получим формулу

. (9)

Интеграл, стоящий в правой части формулы, называется интегралом Дирихле.

III. Предположим, что функция кусочно-непрерывна на отрезке .

Положим в формуле (9) , тогда , , , при . Следовательно, при любом , и мы получаем тождество

. (10)

Умножая обе части равенства (10) на и подводя под знак интеграла, получим равенство

.

Вычтем члены последнего равенства из соответствующих членов равенства (9), получим

.

Таким образом, сходимость ряда Фурье к значению функции в данной точке зависит от того, будет ли интеграл, стоящий справа, стремиться к нулю при .

Разобъем последний интеграл на два интеграла:

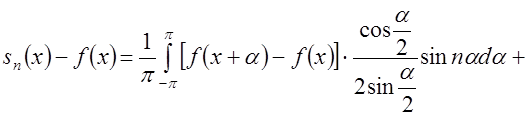
, воспользовавшись тем, что . Разобъем первый из интегралов, стоящих в правой части последнего равенства, на три интеграла:

.

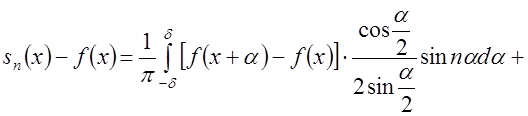
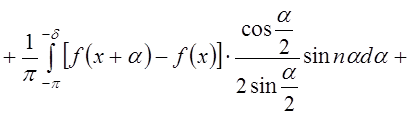
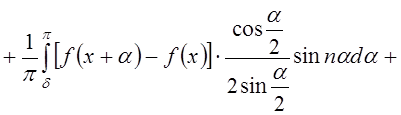
Положим Так как - ограниченная кусочно-непрерывная функция, то - также ограниченная кусочно-непрерывная периодическая функция от . Следовательно, последний интеграл стремиться к нулю при , так как он является коэффициентом Фурье от этой функции. Функция

ограничена при и при и

, где - верхняя граница величины . Кроме того, функция является также кусочно-непрерывной. Следовательно, на основании формул

, .

второй и третий интеграл стремятся к нулю при .

Таким образом, можно написать

.

В выражении стоящем справа, интегрирование производится по промежутку следовательно, интеграл зависит от значений функции только на промежутке от до . Таким образом, из последнего равенства следует важное предложение: сходимость рядов Фурье в данной точке зависит лишь от поведения функции в как угодно малой окрестности этой точки.

В этом заключается так называемый принцип локализации при исследовании рядов Фурье:

Если две функции и совпадают в окрестности некоторой точки , то их ряды Фурье одновременно либо сходятся, либо расходятся в данной точке.

Признак Дини. Ряд Фурье функции в точке сходится к сумме , если при некотором интеграл , где существует.