Оглавление
9. Теорема А.Г. Витушкина об оценке энтропии аналитических функций
Пусть, как и выше, ![]() – область комплексной
плоскости, ограниченная эллипсом
– область комплексной
плоскости, ограниченная эллипсом ![]() с фокусами
с фокусами ![]() и 1 и суммой полуосей
и 1 и суммой полуосей ![]() , и пусть при
, и пусть при ![]() и
и ![]() класс
класс ![]() состоит из всех
вещественных аналитических на отрезке
состоит из всех
вещественных аналитических на отрезке ![]() функций
функций ![]() , для которых существуют аналитические продолжения
, для которых существуют аналитические продолжения ![]() в области
в области ![]() с
с ![]() при
при ![]() .
.
Будем считать также, что в пространстве ![]() определена метрика
определена метрика
![]()
![]() .
.
Тогда
справедлива
Теорема.
При любых ![]() и
и ![]() для
для ![]() -энтропии метрического пространства
-энтропии метрического пространства ![]() имеет место
соотношение эквивалентности
имеет место
соотношение эквивалентности
![]() ~
~
![]() .
.
Доказательство. По основной теореме
об энтропиях для фиксированных ![]() и
и ![]() при любом
при любом ![]() выполняется
неравенство
выполняется
неравенство
![]() .
.
Более того,
если на отрезке ![]() определить
вспомогательные пространства рядов по полиномам Чебышева
определить
вспомогательные пространства рядов по полиномам Чебышева
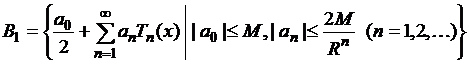 ,
,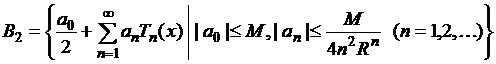
то по леммам 1 и 2 из предыдущего параграфа получим ![]() (заметим, что на этих пространствах
определена одна и та же метрика). Отсюда в силу монотонности по множеству
(заметим, что на этих пространствах
определена одна и та же метрика). Отсюда в силу монотонности по множеству ![]() -емкости и
-емкости и ![]() -энтропии имеем
-энтропии имеем
![]() ,
, ![]() .
.
Для оценки ![]() построим
построим ![]() -сеть для
-сеть для ![]() . Для этого, исходя из полиномов Чебышева
. Для этого, исходя из полиномов Чебышева ![]() (
(![]() ), при фиксированных
), при фиксированных ![]() и натуральном
и натуральном ![]() (значения
(значения ![]() и
и ![]() подберем ниже)
построим полиномы вида
подберем ниже)
построим полиномы вида
 ,
,
где ![]() - некоторые целые
числа. Эти числа
- некоторые целые
числа. Эти числа ![]() подбираем экономно
так, чтобы полиномы
подбираем экономно
так, чтобы полиномы ![]() принадлежали
принадлежали ![]() .
.
Для этого
достаточно потребовать выполнения следующих условий:
![]() ,
,
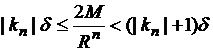 (
(![]() ),
),
а значит, должны выполняться неравенства
![]() ,
, 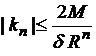 (
(![]() ). (1)
). (1)
Выясним
теперь, при каких значениях ![]() и
и ![]() семейство
семейство ![]() образует
образует ![]() -сеть для множества
-сеть для множества ![]() .
.
Возьмем из
пространства ![]() произвольный ряд
произвольный ряд
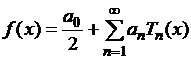 .
.
Подберем
целые числа ![]() (
(![]() ) так, чтобы выполнялось неравенство
) так, чтобы выполнялось неравенство
![]() .
.
Тогда для ![]() с такими
с такими ![]() получим
получим

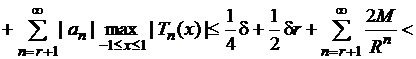
 .
.
Выберем ![]() и
и ![]() так, чтобы
так, чтобы ![]() и
и  . Тогда
. Тогда
 ,
, 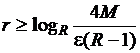 .
.
Значит, можно взять ![]() ,
, 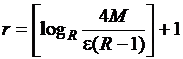 , чтобы получить
, чтобы получить
![]() ,
,
т.е. чтобы семейство полиномов ![]() образовало
образовало ![]() -сеть для пространства
-сеть для пространства ![]() .
.
Оценим теперь
минимальное число элементов в ![]() -сети для
-сети для ![]() . Для этого воспользуемся неравенствами (1). Количество
элементов в семействе
. Для этого воспользуемся неравенствами (1). Количество
элементов в семействе ![]() равно количеству
различных упорядоченных наборов целых чисел (
равно количеству
различных упорядоченных наборов целых чисел (![]() ), удовлетворяющих неравенствам (1). Их же количество,
очевидно, не превосходит произведения
), удовлетворяющих неравенствам (1). Их же количество,
очевидно, не превосходит произведения
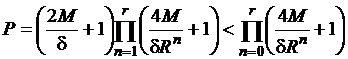 .
.
В силу
достаточной малости ![]() можно считать, что
можно считать, что ![]() . Тогда
. Тогда
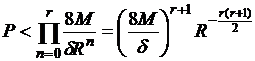 .
.
Следовательно,
подставив значения ![]() ,
, 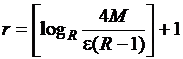 и сохранив главные
члены в оценках, получим
и сохранив главные
члены в оценках, получим
![]()

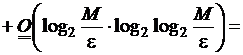

 (
(![]() ).
).
Оценим
теперь снизу ![]() , построив
, построив ![]() -цепь из элементов
-цепь из элементов ![]() , а именно из полиномов вида
, а именно из полиномов вида
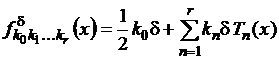 ,
,
причем ![]() , натуральное
, натуральное ![]() и целые коэффициенты
и целые коэффициенты ![]() подберем ниже так,
чтобы в этой
подберем ниже так,
чтобы в этой ![]() -цепи количество
элементов получилось достаточно близким
к количеству элементов максимальной
-цепи количество
элементов получилось достаточно близким
к количеству элементов максимальной ![]() -цепи множества
-цепи множества ![]() .
.
Так как ![]() , должны выполняться неравенства
, должны выполняться неравенства
![]() ,
,  (
(![]() ).
).
Выберем их
так, чтобы выполнялись еще неравенства
![]() ,
, 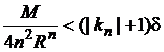 (
(![]() ),
),
а значит, неравенства
![]() ,
, 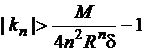 (
(![]() ). (2)
). (2)
Чтобы
элементы ![]() при условии (2)
образовали
при условии (2)
образовали ![]() -цепь, для любых двух различных элементов
-цепь, для любых двух различных элементов ![]() и
и ![]() из них должно
выполняться неравенство
из них должно
выполняться неравенство ![]() . Разность
. Разность ![]() этих элементов
представляет собой некоторый полином вида
этих элементов
представляет собой некоторый полином вида
 ,
,
в котором коэффициенты ![]() целые и не все равны
нулю. Пусть
целые и не все равны
нулю. Пусть ![]() является отличным от
нуля коэффициентом с максимальным номером. Тогда, так как
является отличным от
нуля коэффициентом с максимальным номером. Тогда, так как 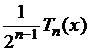 при
при
![]() представляет
собой наименее уклоняющийся от нуля
полином степени
представляет
собой наименее уклоняющийся от нуля
полином степени ![]() со старшим
коэффициентом единица, получим
со старшим
коэффициентом единица, получим ![]() .
.
Согласно
неравенствам (2), количество элементов в максимальной ![]() -цепи множества
-цепи множества ![]() будет больше
произведения
будет больше
произведения

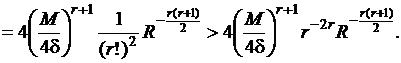
Значит,
![]()
 .
.
Выберем ![]() и
и 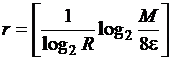 .
.
Тогда
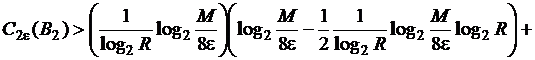
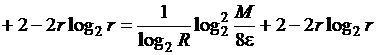 .
.
Следовательно, отсюда и из полученной выше оценки
сверху для ![]() имеем
имеем
![]() ~
~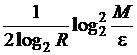
![]() .
.
Теорема
доказана.
Замечание.
Из доказательства теоремы А.Г. Витушкина видно, что
главный член ![]() -энтропии
-энтропии ![]() выделен с помощью
разложений функций
выделен с помощью
разложений функций ![]() в ряды Фурье-Чебышева.
Значит, запоминание коэффициентов Фурье-Чебышева аналитических на отрезке
в ряды Фурье-Чебышева.
Значит, запоминание коэффициентов Фурье-Чебышева аналитических на отрезке ![]() функций оказывается
почти наилучшим способом экономии памяти для записи (табулирования) этих
функций.
функций оказывается
почти наилучшим способом экономии памяти для записи (табулирования) этих
функций.