Оглавление

8. Метод А.Г.Витушкина оценки энтропий аналитических функций

Пусть – эллипс на комплексной плоскости с фокусами и 1 и суммой полуосей , - область, ограниченная эллипсом .

При и через обозначим множество всех вещественных аналитических на отрезке функций , для которых существуют аналитические продолжения в область , причем при .

Через обозначим полином Чебышева степени , который при определяется равенством .

Каждая функция из класса разлагается в равномерно сходящийся на отрезке ряд Фурье-Чебышева

,

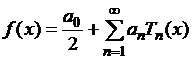где

.

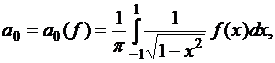
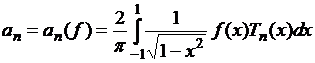
Действительно, положим . Тогда -периодическая функция регулярна на всей действительной оси плоскости переменной .

Покажем, что разлагается в равномерно сходящийся ряд Фурье (по косинусам в силу четности ).

Ряд Фурье для будет равномерно сходящимся на всей оси, так как для ее коэффициентов Фурье (в силу существования непрерывных производных от ) имеем

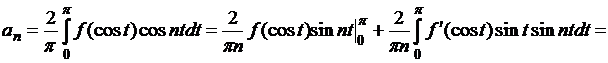
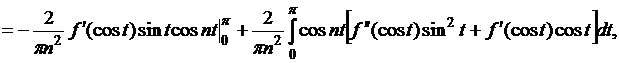
а значит, 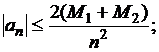здесь , .

Следовательно, ряд Фурье для равномерно на всей оси сходится (по признаку Вейерштрасса), а поэтому сходится к самой функции (в силу свойства полноты системы на ).

Остается заметить, что

;

.

Оказывается, скорость стремления коэффициентов Фурье-Чебышева к нулю при функции из класса почти полностью характеризует саму функцию . Точнее, имеют место следующие две леммы.

Лемма 1. Если при заданных и функция , то для ее коэффициентов Фурье-Чебышева выполняются неравенства

, .

Лемма 2. Если при заданных и коэффициенты ряда (по полиномам Чебышева)

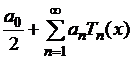
удовлетворяют неравенствам , , то сумма этого ряда .

Образуем теперь два вспомогательных класса рядов по полиномам Чебышева (при заданных и ) следующим образом:

, .

Тогда из лемм 1 и 2 вытекает, что .

Определим в пространстве функций метрику, полагая

,

а в пространствах рядов и определим норму, как максимум модуля суммы ряда 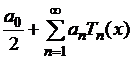на отрезке , и рассмотрим и как метрические пространства с метрикой, порожденной этой максимум-нормой.

Тогда в силу монотонности -энтропии по множеству из соотношений при любом фиксированном вытекают неравенства

.

С другой стороны, по основной теореме об энтропиях для емкости и энтропии выполняется неравенство

.

Если теперь оценить сверху энтропию и снизу емкость , то получим двусторонние оценки для энтропии класса аналитических функций в метрике . В этом заключается основная идея метода А.Г. Витушкина для оценки энтропий классов аналитических функций. По этому методу ниже установлен результат А.Г. Витушкина, а именно найден главный член асимптотики при .

Предварительно остановимся на доказательстве сформулированных выше лемм.

Доказательство леммы 1. Пусть при заданных и функция . Тогда при имеем

.

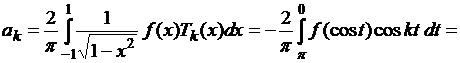
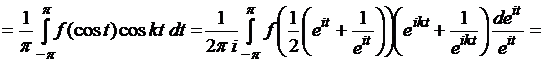
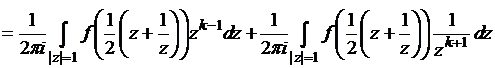Функция регулярна в любом кольце . Возьмем произвольное , для которого . Тогда функция регулярна в кольце , поэтому отображает окружности и в эллипс из области с границей . На эллипсе функция регулярна.

Значит, по свойству аналитических функций получим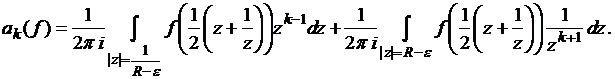

Отсюда, так как точки попадают в область , получим

.

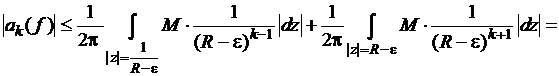
Устремив , получим () .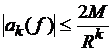

Наконец, .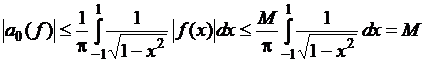

Лемма 1 доказана.

Доказательство леммы 2. Пусть при заданных и для коэффициентов ряда

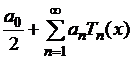(1)

выполняются неравенства

(). (2)

Тогда, так как при , этот ряд сходится равномерно на к некоторой функции . Покажем, что .

Для этого при рассмотрим ряд

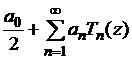(3)

с теми же коэффициентами (), что у ряда (1).

По лемме С.Н.Бернштейна из при вытекает, что при любом и . Тогда в силу условий (2) ряд (3), членами которого являются полиномы, будет равномерно сходиться внутри области к некоторой аналитической в области функции , которая в силу свойства единственности аналитических функций совпадает с функцией (суммой ряда (1)) на отрезке . Остается показать, что при .

Снова по лемме С.Н. Бернштейна при выполняется неравенство (), а значит, при получим

.

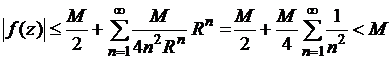Следовательно, .