Оглавление
7. Функции, аналитические на
отрезке
действительной оси
Пусть
![]() определена
на некотором подмножестве
определена
на некотором подмножестве ![]() комплексной плоскости
комплексной плоскости ![]() с предельной точкой
с предельной точкой ![]() . Тогда производной функции
. Тогда производной функции ![]() в точке
в точке ![]() (по множеству
(по множеству ![]() ) называется предел (конечный)
) называется предел (конечный)
 .
.
Функция ![]() называется дифференцируемой
в точке
называется дифференцируемой
в точке ![]() , если
, если ![]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![]() и для ее
приращения выполняется соотношение
и для ее
приращения выполняется соотношение
![]() ,
,
где
![]() не зависит от
не зависит от ![]() ,
, ![]() при
при ![]() .
.
Легко показать, что в случае
дифференцируемости функции ![]() в точке
в точке ![]() выполняется равенство
выполняется равенство ![]() .
.
Теорема. Для того чтобы функция ![]() , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки ![]() , была дифференцируемой в этой точке
, была дифференцируемой в этой точке ![]() , необходимо и достаточно, чтобы функции
, необходимо и достаточно, чтобы функции ![]() и
и ![]() были дифференцируемы в точке
были дифференцируемы в точке ![]() (как функции двух
действительных переменных) и чтобы выполнялись, кроме того, условия Коши-Римана
(как функции двух
действительных переменных) и чтобы выполнялись, кроме того, условия Коши-Римана
 .
.
При выполнении всех условий теоремы
производную ![]() можно вычислять по
различным формулам:
можно вычислять по
различным формулам:
 .
.
Функция ![]() , дифференцируемая в каждой точке некоторого открытого множества
, дифференцируемая в каждой точке некоторого открытого множества ![]() , называется
дифференцируемой на нем, а также голоморфной, аналитической, регулярной.
, называется
дифференцируемой на нем, а также голоморфной, аналитической, регулярной.
Функция ![]() называется
аналитической на произвольном множестве
называется
аналитической на произвольном множестве ![]() , если она аналитична на некотором
открытом множестве
, если она аналитична на некотором
открытом множестве ![]() .
.
Значит, если функция ![]() аналитическая на
отрезке
аналитическая на
отрезке ![]() , то она аналитическая в некоторой круговой окрестности
, то она аналитическая в некоторой круговой окрестности ![]() каждой точки
каждой точки ![]() . Из покрытия отрезка
. Из покрытия отрезка ![]() этими окрестностями
можно выделить конечное подпокрытие, причем эта конечная система окрестностей
из покрытия отрезка
этими окрестностями
можно выделить конечное подпокрытие, причем эта конечная система окрестностей
из покрытия отрезка ![]() будет служить
покрытием некоторого прямоугольника, содержащего отрезок
будет служить
покрытием некоторого прямоугольника, содержащего отрезок ![]() внутри себя. Поэтому
внутри себя. Поэтому ![]() будет аналитической в
области, ограниченной некоторым эллипсом с фокусами в точках
будет аналитической в
области, ограниченной некоторым эллипсом с фокусами в точках ![]() и
и ![]() . Действительно, сначала строим прямоугольник, который
симметричен относительно
. Действительно, сначала строим прямоугольник, который
симметричен относительно ![]() , внутри себя содержит этот отрезок
, внутри себя содержит этот отрезок ![]() и расположен внутри «конечного подпокрытия».
Затем в полученный прямоугольник
вписываем эллипс:
и расположен внутри «конечного подпокрытия».
Затем в полученный прямоугольник
вписываем эллипс:
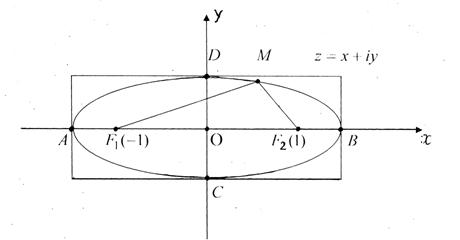
![]() ;
; ![]() ,
, ![]()
![]()
![]() ;
; ![]()
![]()
![]() .
. ![]()
![]()
![]() (
(![]() и
и ![]() могут быть разными,
могут быть разными, ![]() ).
).
Поэтому вместо класса функций, аналитических
на отрезке ![]() , рассматривается
класс однозначных функций, аналитических в области, ограниченной некоторым
эллипсом
, рассматривается
класс однозначных функций, аналитических в области, ограниченной некоторым
эллипсом ![]() с полусуммой осей
с полусуммой осей ![]() .
.
Комплексные функции, как и действительные,
бывают и многозначные. В частности, нам придется иметь дело с функцией
![]() .
.
Она двузначная, поэтому ее нельзя в
окрестности нуля обычным путем разложить в степенной ряд. Дело в том, что сумма
сходящегося степенного ряда не может быть двузначной функции (в силу
единственности предела частичной суммы в любой точке сходимости). Из этой
двузначной функции можно построить разные однозначные функции путем выбора
одного из двух значений в каждой точке (таких способов бесконечно много), но
они не всегда будут аналитическими.
Оказывается, есть способ, когда путем выбора
значений двузначной функции ![]() можно построить ровно
две однозначные аналитические функции
можно построить ровно
две однозначные аналитические функции ![]() и
и ![]() , которые называются регулярными ветвями функции
, которые называются регулярными ветвями функции ![]() или ее однозначными
аналитическими ветвями.
или ее однозначными
аналитическими ветвями.
Для этого рассмотрим обратную функцию,
которую в данном случае можно найти так:
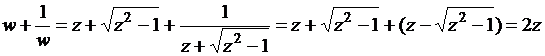 ;
;  .
.
Эта функция называется функцией Жуковского, который нашел
важные применения ее в гидродинамике.
Введем обозначения ![]() ,
, ![]() . Тогда
. Тогда
 .
.
Отсюда 
Значит, окружность ![]() (фиксируем
(фиксируем ![]() и меняем
и меняем ![]() ) функцией Жуковского отображается на эллипс с суммой
полуосей
) функцией Жуковского отображается на эллипс с суммой
полуосей ![]() .
.
На этот же эллипс отображается и другая окружность ![]() .
.
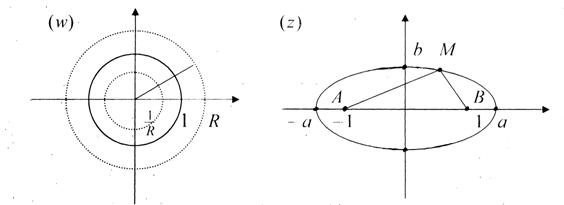
Следовательно,
если взять всевозможные окружности ![]() при
при
![]() , то получим, что функция
, то получим, что функция 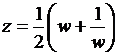 отображает внешность
единичного круга плоскости
отображает внешность
единичного круга плоскости ![]() на внешность отрезка
на внешность отрезка ![]() плоскости
плоскости ![]() .
.
Если же взять
всевозможные окружности ![]() при
при
![]() , то получается отображение функцией
, то получается отображение функцией
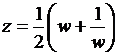 внутренности
единичного круга плоскости
внутренности
единичного круга плоскости ![]() на ту же область –
внешность отрезка
на ту же область –
внешность отрезка ![]() плоскости
плоскости ![]() (
(![]() соответствует
соответствует ![]() ).
).
Отсюда
вытекает следующий способ построения однозначных аналитических ветвей функции ![]() .
.
Исключим из
плоскости ![]() отрезок
отрезок ![]() и рассмотрим для
полученной области:
и рассмотрим для
полученной области:
а) ее
отображение ![]() на внешность
единичного круга плоскости
на внешность
единичного круга плоскости ![]() ;
;
б) ее
отображение ![]() на внутренность
единичного круга плоскости
на внутренность
единичного круга плоскости ![]() .
.
Каждое из
этих отображений однозначно, но формально задается одной и той же формулой, а
именно ![]() (хотя при нахождении
значения корня берутся разные значения для разных ветвей).
(хотя при нахождении
значения корня берутся разные значения для разных ветвей).
При этом
прямая функция 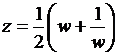 имеет производную
имеет производную  при
при
![]() . Поэтому обратные функции
. Поэтому обратные функции ![]() и
и ![]() имеют (конечные)
производные во всех соответствующих точках (вне отрезка
имеют (конечные)
производные во всех соответствующих точках (вне отрезка ![]() ).
).
Как
приложение этих функций получим оценку модуля алгебраического полинома ![]() , зная
, зная ![]() при
при
![]() .
.
Лемма
(С.Н. Бернштейн). Если алгебраический полином ![]() степени
степени ![]() (
(![]() ) при
) при ![]() удовлетворяет
неравенству
удовлетворяет
неравенству ![]() ,
, ![]() – эллипс с фокусами
– эллипс с фокусами ![]() и 1 и суммой полуосей
и 1 и суммой полуосей ![]() , то
, то
![]() ,
, ![]() .
.
Доказательство. Пусть ![]() регулярная ветвь,
которая отображает внешность отрезка
регулярная ветвь,
которая отображает внешность отрезка ![]() действительной оси
плоскости переменной
действительной оси
плоскости переменной ![]() на внешность единичного
круга плоскости переменной
на внешность единичного
круга плоскости переменной ![]() . Этот отрезок
. Этот отрезок ![]() служит границей
области аналитичности также для вспомогательной
функции
служит границей
области аналитичности также для вспомогательной
функции
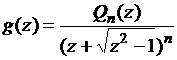 .
.
Поэтому
максимум ее модуля достигается на этой границе, а значит,
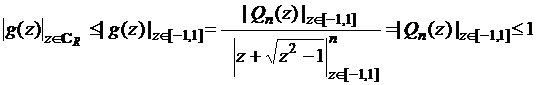 .
.
Отсюда 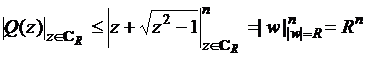 .
.