Оглавление

6. Оценка энтропий подмножеств евклидовых

пространств

Пусть , , …, – данные метрические пространства. Возьмем декартово произведение их носителей

.

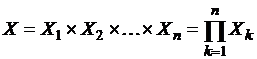Тогда для элементов , , … множества определяются различные метрики. Например, можно взять

. (1)

Аксиомы метрики легко проверяются; эта метрика называется метрикой Хаусдорфа.

Метрику на можно определить и следующим образом:

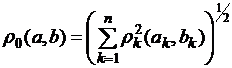. (2)

Пусть теперь ()– компактные метрические пространства, энтропии которых известны. Как оценить энтропию их декартова произведения , например, относительно метрики (1)?

Ясно, что метрики (1) и (2) эквивалентны, т.е. связаны неравенствами для .

Имеет место

Теорема 1. Если 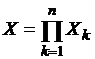– декартово произведение носителей компактных пространств (), то для пространства с метрикой , определяемой равенством (1), при любом выполняются неравенства

.

Доказательство для краткости проведем при .

Для оценки сверху обозначим , . Пусть и – наилучшие -покрытия пространств и соответственно. Тогда легко увидеть, что всевозможные декартовы произведения вида () образуют -покрытие пространства , причем число множеств равно .

Значит, , и требуемая оценка сверху получена.

Чтобы получить нижнюю оценку для , оценим сначала снизу , а затем воспользуемся основной теоремой об энтропиях. Покажем, что

.

Пусть и образуют максимальные -цепи из элементов пространств и соответственно. Тогда всевозможные пары () принадлежат и число таких пар равно .

Покажем, что они образуют в некоторую -цепь.

Действительно, если , то по определению декартова произведения должно выполняться хотя бы одно из неравенств и . Пусть, например, . Тогда и

.

Значит, для числа элементов в максимальной -цепи пространства получим неравенство , поэтому

_. Отсюда и из основной теоремы об энтропиях получим

.

Теорема 1 при доказана (случай произвольного доказывается вполне аналогично).

Как приложение теоремы 1 получим оценки А.Н. Колмогорова для энтропий ограниченных подмножеств из , имеющих внутренние точки (т.е. -мерных ограниченных областей).

Пусть сначала – отрезок с обычной метрикой () и пусть – заданное число.

Найдем минимальное количество отрезков длины (диаметра) , покрывающих весь . Ясно, что надо брать отрезки максимально допустимой длины (с точностью до одного!). Если – максимально возможное число равных отрезков длины , то получим , т.е. , но .

Найдем максимальное количество точек в -цепи из .

Если взять равноотстоящих (на расстоянии ) точек, то получим , т.е. .

Если уменьшить на 1, то , значит, .

Так как не зависит от ( – длина наперед заданного отрезка ), имеем

,

.

Если теперь – некоторый -мерный куб, то отсюда по теореме 1 (для общего случая) получим оценки метрической энтропии (аналогичные оценки, очевидно, получаются для емкости)

,

где и при , т.е. некоторые ограниченные величины.

Теорема 2 (А.Н. Колмогоров). Если – ограниченное подмножество из (-мерного евклидова пространства), имеющее внутренние точки, то для -энтропии выполняется соотношение

.

Доказательство. Раз множество ограниченное и имеет внутренние точки, то найдутся два -мерных куба и таких, что

.

В силу монотонности энтропий по множеству отсюда при имеем

.

Значит,

при

(так как для любого куба, независимо от величины его ребра, выполняется это же соотношение).

Замечание. В силу эквивалентности метрик и аналогичное соотношение с точностью до постоянного множителя можно вывести и для метрики . Но для получения асимптотически точной оценки для метрики расчеты следует провести в самой метрике (а не в ).