Оглавление

14. Оценка метрической энтропии классов функций в метрике 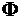-вариаций

Пусть – строго возрастающая допустимая функция с . Фиксируем две функции и типа модуля непрерывности (т.е. неубывающие, непрерывные и полуаддитивные сверху при функции, обращающиеся в нуль при ), причем будем считать и возрастающими при и стремящимися к нулю при .

При определим классы функций

,

.

В [7] доказаны следующие неравенства для оценки -энтропии этих классов в метрике пространства :

1)

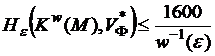
(здесь - функция, обратная к );

2)

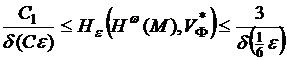
( – решение уравнения , и не зависят от ).

Там же при дополнительных условиях: 1) произведение является функцией типа модуля непрерывности и 2) слабо эквивалентно (при ) получено соотношение слабой эквивалентности -энтропии величине (при ).

Проще доказывается следующее утверждение.

Теорема. Если для данного модуля непрерывности и допустимой функции отношение 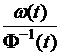является возрастающей функцией при и стремится к нулю при , а – решение уравнения , то для -энтропии класса относительно метрики имеем

при всех достаточно малых и некоторых и , не зависящих от .

Доказательство. Построим -покрытие множества (здесь – это расстояние между элементами в метрике ). Положим , ().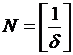

В качестве покрытия возьмем множества , где () – набор целых чисел таких, что функция из принадлежит множеству тогда и только тогда, когда

. (1)

Можно показать, что число различных множеств не превышает .

Поэтому при достаточно малых имеем

,

где не зависит от .

Для получения требуемой оценки остается найти диаметр множества в метрике .

Пусть для взятого набора целых чисел (). Тогда для каждой пары узлов и ввиду (1) выполняются неравенства

. (2)

Для оценки возьмем произвольное разбиение

()

и пусть .

Представим сумму

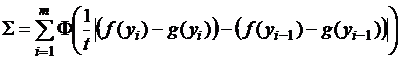
в виде , где распространяется на все слагаемые с парой и , для которых интервал не содержит ни одной из точек (), а сумма распространяется на все остальные слагаемые.

Тогда в силу выпуклости и получим

.

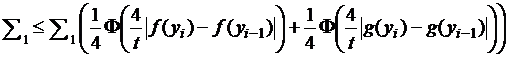Так как в сумме все разности , а функции и , в силу неравенств (см. лемму из §13) 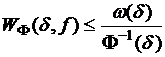, 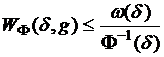получим .

Для оценки суммы для каждого интервала , относящегося к этой сумме, точки из обозначим через . Если теперь , то при получим

.

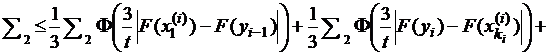
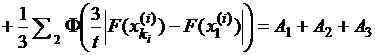При оценке и поступаем по аналогии с оценкой (ввиду и ), что дает и .

Слагаемое отсутствует, когда только одна из точек принадлежит данному интервалу .

Если таких точек больше одной, то применим неравенства (2) и . Тогда

,

а значит,

.

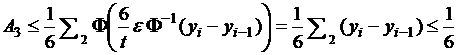Тогда .

Следовательно, для любых двух функций выполняется неравенство

.

Ясно, что все функции из охвачены множествами для различных наборов чисел (), т.е. эти множества образуют -покрытие класса .

Для оценок снизу по заданному достаточно малому берем решение уравнения , натуральное с и строим функции и .

Положим , ; ;

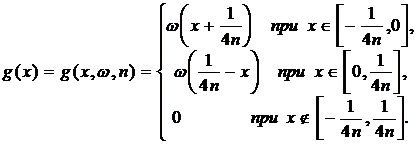
Рассмотрим всевозможные различные функции вида

,

где ().

Ясно, что всего получится таких функций, но среди них при некотором найдется не менее функций вида таких, что для двух и из них выполняется неравенство

.

С другой стороны, очевидно, .

Оценим теперь число -различных функций вида при . Для этого применим равенство . Тогда по выбору и при выполняется неравенство

.

Поэтому

,

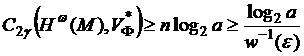где – функция, обратная к .

Отсюда по основной теореме об энтропиях уже легко получить требуемую оценку снизу.