Оглавление
13. Метрика вариаций. Модуль 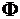 -абсолютной непрерывности
-абсолютной непрерывности
Пусть ![]() – непрерывная,
неубывающая и выпуклая вниз на полуоси
– непрерывная,
неубывающая и выпуклая вниз на полуоси ![]() функция с
функция с ![]() . Всюду ниже такие функции будем называть допустимыми.
. Всюду ниже такие функции будем называть допустимыми.
![]() -вариация функции
-вариация функции ![]() , заданной на отрезке
, заданной на отрезке ![]() , относительно допустимой функции
, относительно допустимой функции ![]() определяется
равенством
определяется
равенством
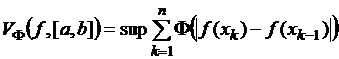 ,
,
где супремум берется по всем конечным разбиениям
![]() (
(![]() ).
).
![]() -вариация введена Л. Юнг и обобщает
-вариация введена Л. Юнг и обобщает ![]() -вариацию Винера, которая совпадает с ней при
-вариацию Винера, которая совпадает с ней при ![]() (
(![]() ); при
); при ![]() получается обычная
жорданова вариация.
получается обычная
жорданова вариация.
Говорят, что ![]() , если
, если ![]() при некотором
при некотором ![]() . Если не различать функции, которые отличаются друг от друга
на отрезке
. Если не различать функции, которые отличаются друг от друга
на отрезке ![]() лишь на константу, то на
лишь на константу, то на ![]() нормой служит
нормой служит
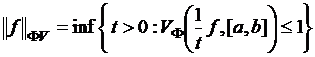 ;
;
![]() становится полным,
вообще говоря, несепарабельным пространством.
становится полным,
вообще говоря, несепарабельным пространством.
Метрика, порождаемая этой нормой, является
более «жесткой» по сравнению с равномерной метрикой, т.е. из сходимости
некоторой последовательности непрерывных функций в метрике, порожденной нормой ![]() , всегда вытекает ее равномерная сходимость на отрезке
, всегда вытекает ее равномерная сходимость на отрезке ![]() ; обратное, вообще говоря, не верно.
; обратное, вообще говоря, не верно.
В силу полноты пространства ![]() предкомпактность
его подмножеств относительно метрики
предкомпактность
его подмножеств относительно метрики ![]() -ваиации будет вытекать из
их полной ограниченности.
-ваиации будет вытекать из
их полной ограниченности.
Модулем ![]() -абсолютной непрерывности функции
-абсолютной непрерывности функции ![]() называется величина
называется величина
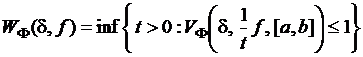 ,
,
где

а
супремум берется по всем разбиениям ![]() с
с
![]()
![]() ;
; ![]()
Функция ![]() называется
называется ![]() -абсолютно непрерывной на отрезке
-абсолютно непрерывной на отрезке ![]() и пишут
и пишут ![]() , если
, если ![]() при
при ![]() .
.
Величина ![]() введена Б.И. Голубовым, а при
введена Б.И. Голубовым, а при ![]() (
(![]() ) – Л. Юнг. Свойства
) – Л. Юнг. Свойства ![]() в случае допустимых
функций
в случае допустимых
функций ![]() общего вида изучены в
[8].
общего вида изучены в
[8].
В частности, какова бы ни была функция ![]() , ее модуль
, ее модуль ![]() -абсолютной
непрерывности
-абсолютной
непрерывности ![]() при всех
при всех ![]() и
и ![]() удовлетворяет
неравенствам
удовлетворяет
неравенствам
![]() .
.
Отсюда
получим
![]() для натуральных
для натуральных ![]() ,
,
![]() для любых
для любых ![]() .
.
Б.И. Голубовым
получен критерий компактности множеств из ![]() относительно метрики
относительно метрики ![]() -вариаций в терминах модуля
-вариаций в терминах модуля ![]() -абсолютной непрерывности в случае, когда допустимая
функция
-абсолютной непрерывности в случае, когда допустимая
функция ![]() удовлетворяет
удовлетворяет ![]() -условию: существуют
-условию: существуют ![]() и
и ![]() такие, что
такие, что ![]() при
при ![]() .
.
В случае допустимых функций ![]() общего вида в [6]
получен признак полной ограниченности (а следовательно, и предкомпатности)
множеств из полного пространства
общего вида в [6]
получен признак полной ограниченности (а следовательно, и предкомпатности)
множеств из полного пространства ![]() в терминах модуля
в терминах модуля ![]() -абсолютной непрерывности.
-абсолютной непрерывности.
Следующее утверждение связывает модуль ![]() -абсолютной непрерывности с обычным равномерным
модулем непрерывности функции и используется при оценке метрической энтропии классов
Гельдера в вариационных метриках.
-абсолютной непрерывности с обычным равномерным
модулем непрерывности функции и используется при оценке метрической энтропии классов
Гельдера в вариационных метриках.
Лемма.
Пусть для возрастающего модуля непрерывности ![]() и допустимой функции
и допустимой функции ![]() отношение
отношение ![]() (
(![]() ) возрастает.
) возрастает.
Тогда для любой функции ![]() (
(![]() ) с равномерным модулем непрерывности
) с равномерным модулем непрерывности ![]() имеем
имеем
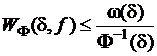 (
(![]() ).
).
Доказательство. Пусть ![]() . Возьмем произвольное
. Возьмем произвольное ![]() и разбиение
и разбиение ![]() с
с ![]()
![]() . Учитывая возрастание функции
. Учитывая возрастание функции ![]() (
(![]() ), при
), при ![]()
![]() требуемое неравенство
получим из соотношений
требуемое неравенство
получим из соотношений

 .
.