Оглавление
12. Оценка энтропий классов
Гельдера в равномерной метрике
Для заданных
функции типа модуля непрерывности ![]() и числа
и числа ![]() определим класс
определим класс
 .
.
Как следует из локальной компактности классов
Гельдера, класс ![]() будет компактным
(относительно равномерной метрики).
будет компактным
(относительно равномерной метрики).
Будем считать ![]() строго возрастающей при
строго возрастающей при ![]() (хотя это не
принципиально: можно вместо
(хотя это не
принципиально: можно вместо ![]() взять каждый раз одно
из решений уравнения
взять каждый раз одно
из решений уравнения ![]() относительно
относительно ![]() ). Тогда справедлива
). Тогда справедлива
Теорема
1. Имеет место соотношение
![]()
 (
(![]() ).
).
Доказательство вытекает из теорем 2 и 3 и
основной теоремы об энтропиях.
Теорема
2. Для данных ф.т.м.н. ![]() и числа
и числа ![]() для
для ![]() -энтропии выполняется неравенство
-энтропии выполняется неравенство
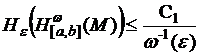 ,
,
где ![]() не зависит от
не зависит от ![]() .
.
Теорема
3. Для данных ф.т.м.н. ![]() и числа
и числа ![]() для
для ![]() -емкости выполняется неравенство
-емкости выполняется неравенство
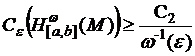 ,
,
где ![]() не зависит от
не зависит от ![]() .
.
Доказательство теоремы 2. Пусть ![]() – данное число и число
– данное число и число
![]() такое, что
такое, что ![]() .
.
Выберем натуральное
![]() так, чтобы
так, чтобы ![]() , и возьмем точки
, и возьмем точки
![]() .
.
Хотим оценить ![]() . Для этого построим
«экономно»
. Для этого построим
«экономно» ![]() -покрытие множества
-покрытие множества ![]() в метрике
в метрике ![]() .
.
Элементы покрытия будем строить исходя из
значений функций из ![]() в точках
в точках ![]() .
.
Через ![]() обозначим
переменные, которые независимо друг от друга могут принимать целые значения из промежутка
обозначим
переменные, которые независимо друг от друга могут принимать целые значения из промежутка ![]() , причем
, причем ![]() подбирается так, чтобы
выполнялись следующие условия:
подбирается так, чтобы
выполнялись следующие условия:
![]() .
.
Образуем множества ![]() (элементы покрытия)
таким образом: берем некоторый набор
(элементы покрытия)
таким образом: берем некоторый набор ![]() допустимых значений и
считаем, что
допустимых значений и
считаем, что
 (*)
(*)
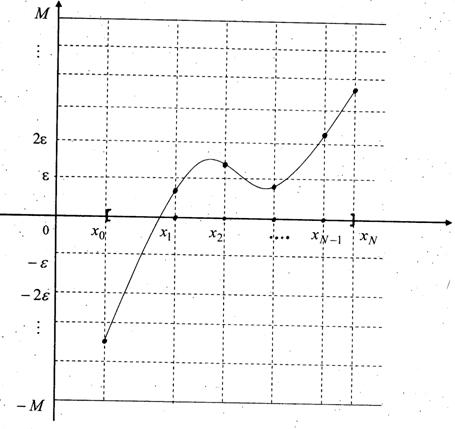
Заметим, что график ![]() пересечет каждую вертикаль
пересечет каждую вертикаль ![]() в пределах от
в пределах от ![]() до
до
![]() . Поэтому для любой такой функции
. Поэтому для любой такой функции ![]() существует хотя бы
один набор (
существует хотя бы
один набор (![]() ), для которого выполняется условие (*), т.е. любая функция
), для которого выполняется условие (*), т.е. любая функция ![]() принадлежит хотя бы
одному элементу покрытия – множеству
принадлежит хотя бы
одному элементу покрытия – множеству ![]() .
.
Оценим ![]() . Возьмем произвольные
. Возьмем произвольные ![]() и
и ![]() , принадлежащие одному и тому же множеству
, принадлежащие одному и тому же множеству ![]() . Тогда на вертикалях
. Тогда на вертикалях ![]() (
(![]() ) по построению покрытия имеем
) по построению покрытия имеем ![]() (
(![]() ) (так как на каждой вертикали
) (так как на каждой вертикали ![]() значения
значения ![]() и
и ![]() расположены на
некотором отрезке длины
расположены на
некотором отрезке длины ![]() ).
).
Пусть теперь ![]() и,
например,
и,
например, ![]() (
(![]() ). Тогда, так как
). Тогда, так как ![]() , получим
, получим
![]()
![]() .
.
Значит, ![]() , т.е. множества
, т.е. множества ![]() образуют
образуют ![]() -покрытие класса
-покрытие класса
![]() .
.
Оценим теперь сверху число непустых множеств вида ![]() . Для этого достаточно оценить сверху количество
упорядоченных наборов (
. Для этого достаточно оценить сверху количество
упорядоченных наборов (![]() ), для которых все значения
), для которых все значения ![]() участвуют в условии
(*) хотя бы для одной функции
участвуют в условии
(*) хотя бы для одной функции ![]() .
.
Оценим количество возможных значений ![]() . По построению вертикальных разбиений отрезка
. По построению вертикальных разбиений отрезка ![]() для максимального
значения переменной
для максимального
значения переменной ![]() должны выполняться
условия:
должны выполняться
условия:
![]()

![]()
![]() .
.
Учитывая значения ![]() , получим, что самое большее
, получим, что самое большее ![]() .
.
Оценим теперь число пар ![]() .
.
Если некоторое значение ![]() фиксировано, то ему
могут соответствовать 5 значений
фиксировано, то ему
могут соответствовать 5 значений ![]() .
.
Действительно, значения переменной ![]() мы берем вдоль
вертикали
мы берем вдоль
вертикали ![]() , на которой
располагаются значения
, на которой
располагаются значения ![]() для всевозможных
функций
для всевозможных
функций ![]() при фиксированном
значении
при фиксированном
значении ![]() на одном из отрезков
на одном из отрезков ![]() на вертикали
на вертикали ![]() .
.
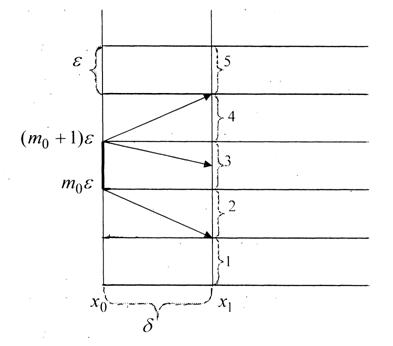
Так как длина промежутка ![]() не превосходит
не превосходит ![]() , в зависимости от функции
, в зависимости от функции ![]() значения
значения ![]() могут участвовать в 5
отрезках длин
могут участвовать в 5
отрезках длин ![]() разбиения на вертикали
разбиения на вертикали
![]() .
.
Значит, упорядоченных пар ![]() самое большее может
быть
самое большее может
быть ![]() .
.
Аналогично, упорядоченных троек ![]() будет самое большее
будет самое большее ![]() и т.д.
и т.д.
Упорядоченных наборов ![]() будет
будет ![]() .
.
Следовательно, минимальное число ![]() элементов в
элементов в ![]() -покрытии множества
-покрытии множества ![]() удовлетворяет
неравенству
удовлетворяет
неравенству
![]() ,
,
а
значит,
 .
.
Оценим ![]() . Имеем (по выбору
. Имеем (по выбору ![]() и
и ![]() )
)
![]()
![]()
![]()
![]()
![]() .
.
При
достаточно малых ![]() получим
получим
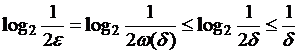 ,
,
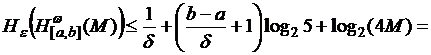
![]()
![]() .
.
У нас ![]() . Тогда
. Тогда ![]() , если существует обратная функция
, если существует обратная функция ![]() ; в общем случае можно считать, что
; в общем случае можно считать, что ![]() – это одно из значений
– это одно из значений
![]() таких, что
таких, что ![]() . Значит, найдется
. Значит, найдется ![]() , не зависящее от
, не зависящее от ![]() , такое, что
, такое, что 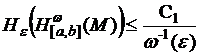 .
.
Доказательство теоремы 3. Пусть, как и выше, ![]()
и
пусть ![]() ,
, ![]() (
(![]() можно считать достаточно малым, чтобы возможно было разбить
отрезок
можно считать достаточно малым, чтобы возможно было разбить
отрезок ![]() на части длины
на части длины ![]() ).
).
Обозначим ![]() . Тогда
. Тогда
![]()
![]()
![]()
![]()
 .
.
Возьмем точки ![]()
![]() и середины
и середины ![]() частичных отрезков
частичных отрезков ![]()
![]() . Построим функции
. Построим функции 
Ясно, что ![]() ,
, ![]() ,
, ![]() .
.
Составим теперь семейство ![]() из функций
из функций ![]() и сумм всевозможных их
сочетаний. Получаются функции следующего вида с различным количеством пиков:
и сумм всевозможных их
сочетаний. Получаются функции следующего вида с различным количеством пиков:
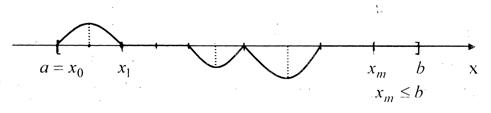
Оценим число различных функций множества ![]() :
:
функций,
имеющих 1 пик, ![]() (с учетом
(с учетом ![]() );
);
функций,
имеющих 2 пика, ![]() ;
;
………………………………….
функций,
имеющих ![]() пиков,
пиков, ![]() .
.
Значит, с учетом тождественного нуля всего
таких функций ![]() .
.
Оценим расстояния между любыми разными
функциями ![]() из
из
![]() :
:
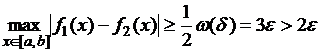 .
.
Следовательно, функции из ![]() образуют
образуют ![]() -цепь и в этой цепи более
-цепь и в этой цепи более ![]() элементов. Поэтому
элементов. Поэтому
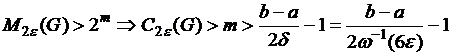 .
.
Здесь, как и выше, ![]() - одно из решений уравнения
- одно из решений уравнения ![]() . Отсюда уже легко следует требуемое неравенство.
. Отсюда уже легко следует требуемое неравенство.