Оглавление
10. Предкомпактные
подмножества пространства 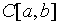
Пусть
![]() – пространство
всех непрерывных на данном отрезке
– пространство
всех непрерывных на данном отрезке ![]() функций
функций ![]() с равномерной нормой
с равномерной нормой
![]() .
.
Эта норма порождает в ![]() равномерную метрику
равномерную метрику
![]()
![]() .
.
Пространство ![]() является одним из
важнейших метрических пространств в анализе.
является одним из
важнейших метрических пространств в анализе.
Как известно, метрическое пространство ![]() называется компактным,
если из любого открытого покрытия множества
называется компактным,
если из любого открытого покрытия множества ![]() можно выделить
конечное подпокрытие или, что то же, если любая
бесконечная последовательность из
можно выделить
конечное подпокрытие или, что то же, если любая
бесконечная последовательность из ![]() имеет хотя бы один
частичный предел, принадлежащий
имеет хотя бы один
частичный предел, принадлежащий ![]() .
.
Для кодируемости
множеств в метрических пространствах достаточным является менее «жесткое»
требование к этим множествам, чем компактность, а именно их предкомпактность.
Множество ![]() в метрическим пространстве
в метрическим пространстве ![]() называется
предкомпактным, если его замыкание
называется
предкомпактным, если его замыкание ![]() в этом пространстве
компактно, т.е. если компактно пространство
в этом пространстве
компактно, т.е. если компактно пространство ![]() .
.
Значит, в случае предкомпактности
![]() в пространстве
в пространстве ![]() любая бесконечная
последовательность из
любая бесконечная
последовательность из ![]() имеет хотя бы один
частичный предел, принадлежащий множеству
имеет хотя бы один
частичный предел, принадлежащий множеству ![]() (и не обязательно
самому множеству
(и не обязательно
самому множеству ![]() ).
).
Отметим также, что в случае подмножеств
полных метрических пространств ![]() предкомпактность
эквивалентна полной ограниченности (т.е. существованию при любом заданном
предкомпактность
эквивалентна полной ограниченности (т.е. существованию при любом заданном ![]() конечной
конечной ![]() -сети).
-сети).
Напомним, что метрическое пространство ![]() называется полным,
если в нем любая фундаментальная последовательность
называется полным,
если в нем любая фундаментальная последовательность ![]() из
из
![]() является сходящейся.
является сходящейся.
Ниже существенно используется
Теорема. В любом полном метрическом пространстве ![]() из предкомпаткности
данного множества
из предкомпаткности
данного множества ![]() вытекает его полная
ограниченность и, обратно, из полной ограниченности множества
вытекает его полная
ограниченность и, обратно, из полной ограниченности множества ![]() вытекает его предкомпактность.
вытекает его предкомпактность.
Доказательство. Если множество ![]() конечно, то оно и предкомпактно, и вполне ограничено. Для доказательства
первого утверждения в случае бесконечных множеств допустим от противного, что
некоторое бесконечное множество
конечно, то оно и предкомпактно, и вполне ограничено. Для доказательства
первого утверждения в случае бесконечных множеств допустим от противного, что
некоторое бесконечное множество ![]() предкомпактно,
но не является вполне ограниченным. Тогда найдется
предкомпактно,
но не является вполне ограниченным. Тогда найдется ![]() такое, что для
такое, что для ![]() не существует конечная
не существует конечная
![]() -сеть. Поэтому найдется бесконечная последовательность
-сеть. Поэтому найдется бесконечная последовательность
![]() из
из ![]() такая, что для любых
двух различных элементов
такая, что для любых
двух различных элементов ![]() и
и ![]() выполняется
неравенство
выполняется
неравенство ![]() (в противном случае
некоторое конечное множество элементов
(в противном случае
некоторое конечное множество элементов ![]() образовало бы конечную
образовало бы конечную
![]() -сеть для
-сеть для ![]() ).
).
Значит, последовательность ![]() не является
фундаментальной, а поэтому ни одна из ее подпоследовательностей
не является
фундаментальной, а поэтому ни одна из ее подпоследовательностей
![]() не может сходиться в
не может сходиться в ![]() , т.е. бесконечная последовательность
, т.е. бесконечная последовательность ![]() не имеет частичных
пределов в
не имеет частичных
пределов в ![]() , что противоречит предкомпактности
множества
, что противоречит предкомпактности
множества ![]() в
в ![]() .
.
Обратно, пусть бесконечное множество ![]() вполне ограничено в
полном метрическом пространстве
вполне ограничено в
полном метрическом пространстве ![]() и докажем, что любая
бесконечная последовательность
и докажем, что любая
бесконечная последовательность ![]() из множества
из множества ![]() имеет хотя бы один
частичный предел, принадлежащий
имеет хотя бы один
частичный предел, принадлежащий ![]() .
.
Возьмем точки из ![]() , образующие конечную
, образующие конечную ![]() -сеть для
-сеть для ![]() , и построим замкнутые шары радиуса
, и построим замкнутые шары радиуса ![]() с центрами в этих
точках. Тогда хотя бы один из этих шаров (их конечное число) содержит
бесконечную подпоследовательность последовательности
с центрами в этих
точках. Тогда хотя бы один из этих шаров (их конечное число) содержит
бесконечную подпоследовательность последовательности ![]() Обозначим их
через
Обозначим их
через ![]()
Заметим, что ![]() для всех
для всех ![]()
Аналогично, построим бесконечную подпоследовательность ![]() последовательности
последовательности ![]() , взяв
, взяв ![]() -сеть для
-сеть для ![]() и замкнутые шары
радиуса
и замкнутые шары
радиуса ![]() с центрами в точках
с центрами в точках ![]() -сети для
-сети для ![]() .
.
Продолжив этот процесс до бесконечности, мы
получим следующую таблицу:
![]()
![]()
……………
![]()
……………
В
ней последовательность в каждой следующей строке является подпоследовательностью
последовательности в предыдущей строке и при любом ![]() выполняется
неравенство
выполняется
неравенство ![]() для всех
для всех ![]() и всех
и всех ![]() , в частности, при
, в частности, при ![]() (
(![]() - любое натуральное) и
- любое натуральное) и ![]() .
.
Рассмотрим диагональную последовательность ![]() , которая будет фундаментальной. Действительно, по построению
имеем
, которая будет фундаментальной. Действительно, по построению
имеем ![]() , поэтому левая часть стремится к нулю при
, поэтому левая часть стремится к нулю при
![]() , независимо от значения натурального
, независимо от значения натурального ![]() .
.
В силу полноты пространства ![]() последовательность
последовательность ![]() имеет предел,
принадлежащий
имеет предел,
принадлежащий ![]() . Следовательно,
. Следовательно, ![]() предкомпактно
в
предкомпактно
в ![]() .
.
Выясним теперь, какие условия обеспечивают предкомпактность (что то же,
полную ограниченность) подмножеств полного пространства ![]() с равномерной
метрикой.
с равномерной
метрикой.
Напомним, что определенная на данном
множестве ![]() функция
функция ![]() называется:
называется:
1) непрерывной на ![]() , если
, если
![]()
![]() ;
;
2) равномерно непрерывной на ![]() , если
, если
![]() .
.
Семейство функций ![]() , определенных на данном множестве
, определенных на данном множестве ![]() , называется равностепенно непрерывным на
, называется равностепенно непрерывным на ![]() , если
, если
![]()
![]() .
.
Семейство функций ![]() , определенных на множестве
, определенных на множестве ![]() , называется равномерно ограниченным на
, называется равномерно ограниченным на ![]() , если
, если
![]() .
.
Теорема
(Арцела). Для предкомпактности
множества ![]() функций из
пространства
функций из
пространства ![]() с равномерной метрикой
необходимо и достаточно, чтобы на отрезке
с равномерной метрикой
необходимо и достаточно, чтобы на отрезке ![]() множество
множество ![]() было одновременно
было одновременно
1) равномерно ограниченным,
2) равностепенно непрерывным.
Доказательство. Необходимость. Пусть
множество ![]() из
из ![]() предкомпактно.
Тогда множество
предкомпактно.
Тогда множество ![]() вполне ограничено.
Поэтому при
вполне ограничено.
Поэтому при ![]() для
для ![]() существует конечная
существует конечная ![]() -сеть функций
-сеть функций ![]() из
из ![]() , а значит, для любой
, а значит, для любой ![]() найдется
найдется ![]() такая, что
такая, что ![]() .
.
Отсюда, если обозначить ![]() , получим
, получим ![]() , т.е. множество
, т.е. множество ![]() равномерно ограничено.
равномерно ограничено.
Для доказательства равностепенной
непрерывности множества ![]() на
на ![]() возьмем произвольное
возьмем произвольное ![]() и соответствующую
и соответствующую ![]() -сеть
-сеть ![]() из
из ![]() .
.
В силу равномерной непрерывности ![]() (
(![]() ) на отрезке
) на отрезке ![]() найдется
найдется ![]() такое, что для любых
такое, что для любых ![]() с
с ![]() выполняется
неравенство
выполняется
неравенство ![]() .
.
Положим ![]() . Тогда для любой функции
. Тогда для любой функции ![]() и любых
и любых ![]() с
с
![]() получим
получим
![]() ,
,
если
![]() .
.
Значит, множество функций ![]() равностепенно
непрерывно на
равностепенно
непрерывно на ![]() .
.
Достаточность. Пусть множество
функций ![]() из
из
![]() на отрезке
на отрезке ![]() одновременно равномерно ограничено и
равностепенно непрерывно. Тогда существует число
одновременно равномерно ограничено и
равностепенно непрерывно. Тогда существует число ![]() такое, что
такое, что ![]() для любой функции
для любой функции ![]() и любой точки
и любой точки ![]() .
.
Возьмем произвольное ![]() и покажем, что в
и покажем, что в ![]() существует конечная
существует конечная ![]() -сеть для множества
-сеть для множества ![]() . Искомую
. Искомую ![]() -сеть построим из ломаных, непрерывных на отрезке
-сеть построим из ломаных, непрерывных на отрезке ![]() . Для этого возьмем
. Для этого возьмем ![]() такое, что для любых
такое, что для любых ![]() с
с ![]() вытекает
вытекает ![]() для любой функции
для любой функции ![]() .
.
Возьмем конечные разбиения ![]() и
и ![]() такие, что
такие, что ![]() (
(![]() ) и
) и ![]() (
(![]() ). Построим прямоугольную сетку с помощью прямых
). Построим прямоугольную сетку с помощью прямых
![]() (
(![]() ) и
) и ![]() (
(![]() ).
).
Так как получится сетка с конечным числом
узлов, всевозможных ломаных с вершинами в этих узлах также будет конечное
число. Они образуют ![]() -сеть для множества
-сеть для множества ![]() .
.
Действительно, если ![]() , то выберем ломаную
, то выберем ломаную ![]() следующим образом:
точка
следующим образом:
точка ![]() является вершиной
ломаной
является вершиной
ломаной ![]() , если выполнено условие
, если выполнено условие ![]() .
.
Тогда для любой точки ![]() получим
получим
![]()
![]()
![]() .
.
Значит,
![]() .
.