§ 9. Основные свойства интеграла Лебега от ограниченной
измеримой функции
В
этом параграфе речь идет лишь об интегралах по ограниченным множествам.
Следующее
утверждение называется теоремой о среднем
для интеграла Лебега.
![]() . Если функция
. Если функция ![]() измерима на данном
множестве
измерима на данном
множестве ![]() и
и ![]() для данных
для данных ![]() и
и ![]() , то выполняется неравенство
, то выполняется неравенство
![]() .
(1)
.
(1)
Отметим
некоторые важные следствия из неравенства (1).
1)
Если функция ![]() (
(![]() ) постоянна, то
) постоянна, то ![]() .
.
Для
доказательства достаточно в неравенстве (1) взять ![]() ; измеримость функции
; измеримость функции ![]() очевидна.
очевидна.
2)
Если ![]() , то для любой функции
, то для любой функции ![]() , определенной на
, определенной на ![]() , интеграл равен нулю:
, интеграл равен нулю: ![]() .
.
3)
Если ![]() и
и ![]() ограничена
и измерима на
ограничена
и измерима на ![]() , то
, то ![]() ; если же
; если же ![]() , то
, то ![]() .
.
Следующее
свойство называется полной аддитивностью интеграла.
![]() . Если (ограниченное) множество
. Если (ограниченное) множество ![]() представляет собой
объединение
представляет собой
объединение ![]() конечного или счетного
множества непересекающихся между собой измеримых множеств
конечного или счетного
множества непересекающихся между собой измеримых множеств ![]() , то для любой ограниченной измеримой на
, то для любой ограниченной измеримой на ![]() функции
функции ![]() выполняется равенство:
выполняется равенство:
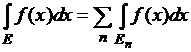 .
.
![]() Если две ограниченные
измеримые функции эквивалентны между собой
Если две ограниченные
измеримые функции эквивалентны между собой ![]() на множестве
на множестве ![]() , то
, то ![]()
Действительно,
по определению эквивалентности функций ![]() . Тогда для множеств
. Тогда для множеств ![]() и
и ![]() получим равенства
получим равенства 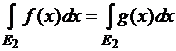 ,
, 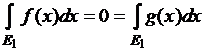 . Остается почленно сложить эти
равенства.
. Остается почленно сложить эти
равенства.
![]() Интеграл Лебега
обладает линейностью: если две
функции
Интеграл Лебега
обладает линейностью: если две
функции ![]() и
и ![]() ограничены и измеримы
на данном множестве
ограничены и измеримы
на данном множестве ![]() , то для любых действительных чисел
, то для любых действительных чисел ![]() и
и ![]() выполняется равенство
выполняется равенство
![]() .
.
![]() Если для ограниченной измеримой на
Если для ограниченной измеримой на ![]() функции
функции ![]() выполняется неравенство
выполняется неравенство
![]() (
(![]() ), то
), то ![]() .
.
Отсюда
уже легко следует монотонность интеграла
Лебега: если две ограниченные измеримые на ![]() функции удовлетворяют
неравенству
функции удовлетворяют
неравенству ![]() (
(![]() ), то
), то ![]()
![]() Если функция
Если функция ![]() ограничена и измерима
на множестве
ограничена и измерима
на множестве ![]() , то
, то  .
.
![]() Если для измеримых на множестве
Если для измеримых на множестве ![]() функций
функций ![]() (
(![]() ) существует число
) существует число ![]() такое, что
такое, что ![]() (для любого
(для любого ![]() ;
; ![]() ), и существует
), и существует ![]() для почти всех
для почти всех ![]() , то выполняется равенство
, то выполняется равенство
![]() .
.
Как следует из
приведенных выше свойств, интеграл Лебега обладает всеми важными свойствами
обычного интеграла (аддитивностью, линейностью,
монотонностью и т.д.). Однако интеграл Лебега обладает свойством ![]() , которое позволяет достаточно свободно перейти к пределу под
знаком интеграла. Именно это свойство интеграла Лебега делает его удобным инструментом
в различных исследованиях.
, которое позволяет достаточно свободно перейти к пределу под
знаком интеграла. Именно это свойство интеграла Лебега делает его удобным инструментом
в различных исследованиях.
Оглавление