§ 8. Интеграл Лебега от ограниченной измеримой функции

Пусть ограничена и измерима на ограниченном множестве . В силу ограниченности существуют конечные числа и . Возьмем произвольное разбиение отрезка (по оси ) . Тогда множества , , также будут измеримы, т.е. существуют лебеговы меры (), и для разбиения можно определить соответственно нижнюю и верхнюю суммы Лебега и .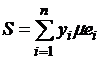

Аналогично свойствам сумм Дарбу доказываются следующие свойства сумм Лебега:

1) при добавлении новых точек разбиения нижние суммы не уменьшаются, а верхние не увеличиваются;

2) любая нижняя сумма не превосходит любой верхней суммы , т.е. .

Следовательно, для всевозможных разбиений множество нижних сумм Лебега ограничено сверху, а множество верхних сумм ограничено снизу. Поэтому существуют конечные точные границы и .

Общее значение этих точных границ называется интегралом Лебега от функции по множеству и обозначается так: или .

Известно, что интегралы Дарбу и не для всякой ограниченной на данном отрезке функции совпадают между собой. Как будет доказано ниже, значения и совпадают между собой для любой ограниченной измеримой на множестве E функции ; другими словами, интеграл Лебега существует и конечен в случае любой ограниченной измеримой функции.

Действительно, по аналогии с интегралами Дарбу легко получается неравенство для любого разбиения . Отсюда получим .

Определим теперь шаг разбиения . Тогда получим .

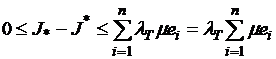Заметим, что множества попарно не пересекаются между собой и 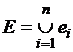. В силу аддитивности меры Лебега получим равенство .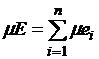

Следовательно, выполняется неравенство .

Так как шаг разбиения можно выбрать сколь угодно малым, отсюда получим или , т.е. интеграл Лебега существует и конечен.

Заметим, что в случае для интегралов Лебега принято также обозначение 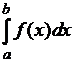. Чтобы различать интегралы Римана и Лебега, приняты обозначения: 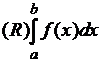(для интеграла Римана), (для интеграла Лебега).

Оглавление