§ 7. Некоторые замечания об определении интеграла Римана

Приведем два эквивалентных определения интеграла Римана от функции по отрезку .

1) Пусть определена на данном отрезке . Возьмем произвольное разбиение этого отрезка . Обозначим и найдем шаг разбиения . Выберем произвольным образом точки (). Тогда следующий предел интегральных сумм и называется интегралом Римана:

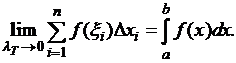
2) Определим теперь суммы Дарбу для функции и разбиения . Пусть , (). Тогда нижняя и верхняя суммы Дарбу, как известно, определяются соответственно равенствам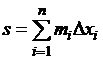и и .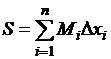

Известно также, что возрастает и убывает при добавлении новых точек разбиения; множества сумм {} и {} для всевозможных конечных разбиений T отрезка ограничены сверху и снизу соответственно. Поэтому существуют конечные точные границы , которые называются интегралами Дарбу.

Легко показать, что для ограниченной на данном отрезке функции интегралы Дарбу всегда существуют, но не всегда равны между собой. Интегралы Дарбу совпадают между собой и их общее значение совпадает с интегралом Римана тогда и только тогда, когда этот интеграл существует.

Следовательно, интеграл Римана от ограниченной на данном отрезке функции можно определить как общее значение интегралов Дарбу от этой функции на отрезке .

Как увидим ниже, это второе определение интеграла Римана позволяет лучше понять его отличие от интеграла Лебега (в случае отрезка).

Оглавление