§ 6. Свойства измеримых функций

Приведем основные свойства измеримых функций.

1) Если - измеримое подмножество данного множества , а функция измерима на , то измерима и на .

Действительно, при имеем .

2) Если мера Лебега, то любая функция , определенная на множестве , измерима на .

В самом деле, измеримость на означает, что измеримы все множества вида и само множество . У нас , а поэтому все множества вида как подмножества этого множества также имеют нулевую меру, т.е. функция измерима на .

Две функции и , определенные на данном множестве , называются эквивалентными на , если ; в этом случае говорят также, что почти всюду на или пишут ().

3) Если функция измерима на множестве и (), то функция также измерима на .

Действительно, при выполняется равенство .

Находя отдельно меры левой и правой частей этого равенства и учитывая равенство , получим .

Приведем один пример на применение этого свойства измеримых функций, а именно покажем, что функция 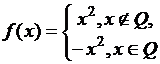является измеримой на отрезке .

Как известно, (так как – счетное множество), поэтому ().

Известно также, что непрерывная на данном отрезке функция измерима на нем, а поэтому измерима на отрезке .

Следовательно, функция измерима на отрезке .

4) Если функция измерима на данном множестве , то множества и измеримы для любых действительных .

В самом деле, для любых действительных имеем .

Теперь измеримость левых частей этих равенств вытекает из измеримости их правых частей.

5) Если функции и измеримы на данном множестве , то на этом множестве измеримы функции , , (последняя - при на ).

Легко доказать также, что измерима на множестве , если измерима на нем. Это следует из равенства для действительных .

6) Если функции в последовательности измеримы на данном множестве и почти всюду на множестве (т.е. за исключением, быть может, точек его подмножества меры нуль) существует предел , то полученная в пределе функция также измерима на множестве .

Следовательно, по свойству 5) алгебраические операции над функциями не выводят за класс измеримых функций, как и в случае непрерывных функций. Однако, по свойству 6), в противоположность непрерывным функциям, операция поточечного перехода к пределу (даже почти всюду) также сохраняет класс измеримых функций. И, вообще, измеримые функции – это самый широкий класс функций, изучаемых в математическом анализе, причем инвариантный относительно всех допустимых в нем операций.

Оглавление