§ 5. Измеримые функции. Примеры

Если функция определена на данном множестве и - некоторое действительное число, то через будем обозначать множество .

Аналогично при определяются множества , , , , и др.

Пусть функция определена на данном измеримом по Лебегу множестве . Тогда эта функция называется измеримой на множестве , если при всех измеримы множества .

Примеры. 1) Если , то любая функция , определенная на множестве , является измеримой.

2) Постоянная функция является измеримой на любом измеримом множестве .

Действительно, множество при совпадает с измеримым множеством , а при оно пусто, поэтому также измеримо (мера равна нулю).

3) Ступенчатая на данном сегменте функция является измеримой на нем.

Действительно, пусть - все узлы ступенчатой функции и пусть

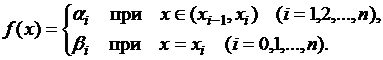
Тогда ясно, что при множество либо пусто, либо представляет собой объединение конечного числа промежутков, т.е. является элементарным множеством. Все элементарные множества являются измеримыми, поэтому любая ступенчатая функция является измеримой.

Заметим, что ступенчатая функция может иметь точки разрыва. Значит, разрывные функции могут быть измеримыми.

4) Легко проверить, что функция на сегменте измерима.

5) Неограниченные функции могут быть измеримыми. Например, функция измерима на полуинтервале .

Действительно, множество совпадает с интервалом и с полуинтервалом . Поэтому оно измеримо при .

6) Функция Дирихле 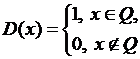измерима на любом сегменте (хотя все точки этого отрезка (при ) являются точками разрыва этой функции).

Действительно, пусть . Тогда

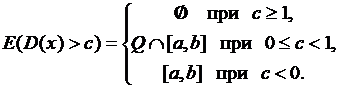
Получили всего три вида измеримых множеств, а поэтому функция Дирихле также измерима.

Значит, всюду разрывная на данном промежутке функция может быть измеримой на нем.

7) Любая функция , непрерывная на данном сегменте , измерима на нем.

Действительно, сегмент обозначим через . Тогда получим . Легко показать, что множество замкнутое. Раз замкнуто и ограничено (как подмножество множества ), оно измеримо.

Значит, множество измеримо при , т.е. функция измерима на .

Изучая вопросы обратимости утверждения 7), Н. Н. Лузин доказал, что измеримая на сегменте функция становится непрерывной, если изменить ее значения на множестве сколь угодно малой меры.

Оглавление