§ 4. Примеры измеримых множеств. Открытые и замкнутые множества

С использованием, в частности, приведенных выше свойств, легко установить измеримость приводимых ниже в примерах числовых множеств.

Пример 1. Любой конечный промежуток (сегмент, интервал или полуинтервал) является измеримым по Лебегу множеством и его мера равна длине этого промежутка.

Пример 2. Любое конечное множество измеримо по Лебегу и его мера равна нулю.

Пример 3. Любое счетное множество измеримо по Лебегу и .

Действительно, одноточечные множества измеримы, а поэтому в случае ограниченного множества можно применить теорему 3 и найти его меру, равную нулю, а затем перейти к пределу.

Измеримость этого множества можно было получить также исходя из определения.

Множество называется открытым, если его можно представить в виде конечного или счетного объединения непересекающихся между собой интервалов: .

Замечание 1. Это определение эквивалентно следующему: множество называется открытым, если существует интервал такой, что .

Множество называется замкнутым, если его дополнение до всей оси является открытым множеством.

Замечание 2. Напомним, что точка называется предельной точкой множества , если любой интервал, содержащий точку , содержит бесконечное множество точек из . Можно доказать, что данное выше определение замкнутого множества эквивалентно следующему: множество называется замкнутым, если оно содержит все свои предельные точки. В частности, если множество конечно, то оно также будет замкнутым (у него нет предельных точек).

Пример 4. Любое открытое ограниченное множество измеримо.

Действительно, по определению это множество представимо в виде конечного или счетного объединения неналегающих интервалов: .

Следовательно, по теореме 3 имеем .

Пример 5. Любое ограниченное замкнутое множество измеримо.

В самом деле, если - наименьший сегмент, содержащий замкнутое множество , а - дополнение множества до всей оси , то выполняется равенство , т.е. множество открыто. Поэтому оно представимо в виде не более счетного объединения неналегающих интервалов: . Отсюда получим

.

Можно привести более общие примеры измеримых множеств. Так, измеримым по Лебегу будет любое борелево множество.

Множество называется борелевым множеством, если его можно получить, исходя из открытых и замкнутых множеств, с помощью применения не более счетного множества операций объединения и пересечения.

Отметим, что существуют неизмеримые по Лебегу ограниченные множества, однако такие множества трудно строятся (примеры неизмеримых множеств можно найти в [2]). Поэтому приведем пример неизмеримого по Жордану (ограниченного) множества.

Пример 6. Множество неизмеримо по Жордану.

Действительно, возьмем любое элементарное множество 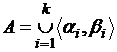и найдем . Получим объединение двух множеств: множества всех иррациональных точек из всех и множества всех рациональных точек из , т.е. получается всюду плотное на множество. Поэтому при нахождении внешней меры Жордана

промежутки должны покрывать весь отрезок , а поэтому их суммарная длина должна быть не меньше единицы. При этом промежуток также покрывает множество , а значит, . Поэтому за счет выбора элементарного множества внешнюю меру Жордана нельзя сделать сколь угодно малой, т.е. множество неизмеримо по Жордану.

Оглавление