§13. Примеры на интегрирование по Лебегу

1) Найти интеграл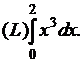

Функция непрерывна на отрезке , поэтому

Аналогично поступаем с любой непрерывной на данном отрезке функцией .

2) Найти интеграл .

Функция интегрируема по Риману. Поэтому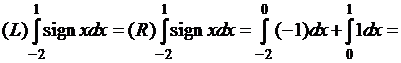

3) Пусть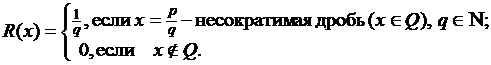

Эта функция непрерывна в иррациональных точках и разрывна в рациональных точках. Но множество рациональных точек счетно, а поэтому для любого отрезка .

Следовательно, ограниченная функция почти всюду на отрезке непрерывна, а поэтому существуют оба интеграла: и 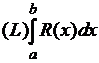. На множестве нулевой меры подынтегральную функцию можно доопределить любым образом (от этого значение интеграла Лебега не меняется), поэтому положим

В результате получили непрерывную функцию . Тогда, очевидно,

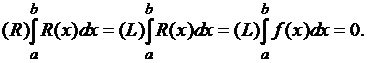
4) Рассмотрим функцию Дирихле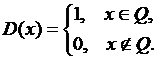

Все точки отрезка (при являются точками разрыва этой функции, поэтому не существует интеграл .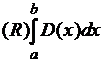

С другой стороны, легко показать, что является ограниченной измеримой функцией, а поэтому существует . Для его нахождения положим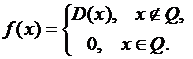

Получили . В силу эквивалентности функций и выполняется равенство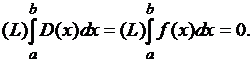

5) Найти интеграл 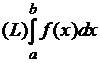, если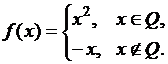

Как и выше, возьмем функцию , эквивалентную функции на данном отрезке . Тогда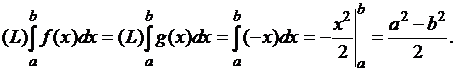

6) Пусть ограничена и измерима на отрезке . Интегрируема ли по Лебегу функция на отрезке ?

Так как функция ограничена на отрезке , то, очевидно, функция также ограничена на нем. Если обозначим , то получим при и при .

Поэтому из измеримости функции вытекает измеримость функции на отрезке .

Раз функция ограничена и измерима на отрезке , она интегрируема по Лебегу на этом отрезке.

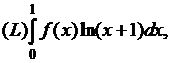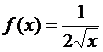7) Найти если при и при .

Функция на отрезке , поэтому .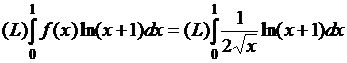

Функции и абсолютно непрерывны на , поэтому, интегрируя по частям, получим

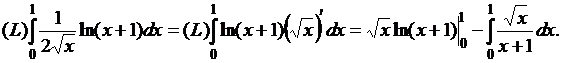
Применив замену переменной , получим искомое значение .

Оглавление