§12. Суммируемые функции (любого знака)
Пусть функция ![]() измерима на данном
множестве
измерима на данном
множестве ![]() . Тогда
. Тогда
(+)-срезкой
и (-)-срезкой
этой функции называются соответственно следующие определенные на множестве ![]() две функции:
две функции:
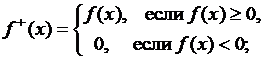
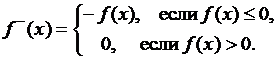


Легко
проверить, что выполняются следующие равенства:
![]() ,
, ![]() ,
, ![]() .
.
Отсюда,
так как из измеримости ![]() на множестве
на множестве ![]() вытекает
измеримость
вытекает
измеримость ![]() на этом множестве,
получим, что на множестве
на этом множестве,
получим, что на множестве ![]() измеримыми будут обе
функции:
измеримыми будут обе
функции: ![]() и
и ![]() . Раз обе срезки являются неотрицательными измеримыми
функциями на множестве
. Раз обе срезки являются неотрицательными измеримыми
функциями на множестве ![]() , то имеют смысл следующие два интеграла Лебега:
, то имеют смысл следующие два интеграла Лебега: 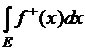 и
и  .
.
Интегралом Лебега от измеримой на данном
множестве ![]() функции
функции ![]() называется следующая
разность интегралов:
называется следующая
разность интегралов:
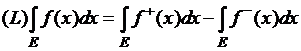 ,
,
если хотя бы один из интегралов в правой части
конечен.
Если
же оба интеграла в правой части конечны, то функция ![]() называется суммируемой
или интегрируемой по Лебегу на множестве
называется суммируемой
или интегрируемой по Лебегу на множестве
![]() .
.
Замечание.
Это же определение интеграла Лебега остается в силе в случае функций
любого знака (ограниченных или неограниченных), измеримых на данном
неограниченном множестве ![]() .
.
Ясно,
что любая ограниченная измеримая на данном ограниченном множестве ![]() функция
функция ![]() будет суммируемой на
этом множестве.
будет суммируемой на
этом множестве.
Как
видно из приводимых ниже утверждений, суммируемые функции обладают свойствами,
аналогичными свойствам ограниченных измеримых функций.
1.
Суммируемые функции обладают линейностью: если функции ![]() и
и ![]() суммируемы на данном
множестве
суммируемы на данном
множестве ![]() , то при любых действительных
, то при любых действительных ![]() и
и ![]() функция
функция ![]() также суммируема на
также суммируема на ![]() и выполняется равенство
и выполняется равенство
![]()
2.
Если функция ![]() суммируема на данном
множестве
суммируема на данном
множестве ![]() , а функция
, а функция ![]() измерима и ограничена
на
измерима и ограничена
на ![]() , то функция
, то функция ![]() суммируема на
суммируема на ![]() .
.
3.
Суммируемые функции обладают полной аддитивностью в
следующей форме: если ![]() суммируема
на множестве
суммируема
на множестве ![]() и это множество представимо
в виде конечного или счетного объединения измеримых непересекающихся множеств
и это множество представимо
в виде конечного или счетного объединения измеримых непересекающихся множеств ![]() , т.е.
, т.е. ![]()
![]() при
при ![]() , то выполняется равенство
, то выполняется равенство
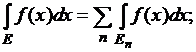
однако
в случае счетного объединения из суммируемости ![]() на всех
на всех ![]() не вытекает
суммируемость
не вытекает
суммируемость ![]() на
на ![]() , хотя в случае конечного объединения вытекает.
, хотя в случае конечного объединения вытекает.
4.
Для измеримых функций сама функция ![]() суммируема на данном
множестве
суммируема на данном
множестве ![]() тогда и только тогда,
когда на нем суммируема функция
тогда и только тогда,
когда на нем суммируема функция ![]() .
.
Напомним,
что такая «жесткая» связь между интегрируемостью самой функции
и ее модуля в интегралах Римана отсутствует. Хотя из интегрируемости по
Риману в собственном смысле самой функции вытекает интегрируемость ее модуля на
рассматриваемом отрезке, обратное утверждение не верно. Так, функция ![]() , равная 1 при
, равная 1 при ![]() и равная
и равная ![]() при
при ![]() , на отрезке
, на отрезке ![]() не интегрируема по
Риману, а функция
не интегрируема по
Риману, а функция ![]() интегрируема на
интегрируема на ![]() .
.
В
общем случае интегралов Римана нет следования и в другом направлении: функция ![]() , равная
, равная ![]() при
при
![]() и равная
и равная ![]() при
при ![]() , на отрезке
, на отрезке ![]() интегрируема по Риману
(в несобственном смысле), а ее модуль
интегрируема по Риману
(в несобственном смысле), а ее модуль ![]() - нет.
- нет.
Заметим,
что построенная функция ![]() на отрезке
на отрезке ![]() измерима, но не суммируема,
т.е. не интегрируема по Лебегу, и при этом интегрируема по Риману в
несобственном смысле.
измерима, но не суммируема,
т.е. не интегрируема по Лебегу, и при этом интегрируема по Риману в
несобственном смысле.
Если
интегрируемость в несобственном смысле не требуется, то еще легче строятся примеры, которые показывают, что не
всякая измеримая функция является суммируемой.
Действительно, пусть 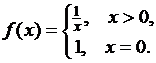 Тогда
Тогда ![]() измерима на отрезке
измерима на отрезке
![]() и при натуральных
и при натуральных ![]() получим:
получим:
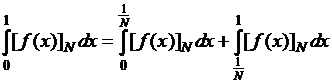
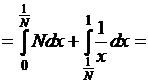

![]() при
при ![]() .
.
Значит,
 . Поэтому данная
функция
. Поэтому данная
функция ![]() не является
суммируемой на отрезке
не является
суммируемой на отрезке ![]() .
.
Приведем теперь пример неограниченной
суммируемой функции. Пусть 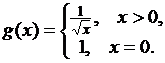 Тогда эта
функция является неотрицательной измеримой на отрезке
Тогда эта
функция является неотрицательной измеримой на отрезке ![]() . При этом
. При этом 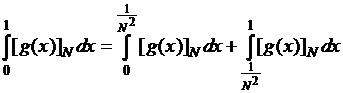
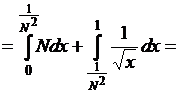

![]() .
.
Значит, 
Следовательно,
эта неограниченная функция является суммируемой на отрезке ![]() .
.
Обратимся
теперь к общему случаю восстановления функции по известной ее производной
интегрированием по Лебегу (т.е. к случаю суммируемых производных, а для ограниченных
производных этот вопрос рассмотрен в § 10).
В общем случае
имеет место
Теорема. Если:
1) при всех ![]() существует конечная производная
существует конечная производная
![]() ; 2)
производная
; 2)
производная ![]() суммируема на
суммируема на ![]() , то для каждого
, то для каждого ![]() выполняется
равенство
выполняется
равенство 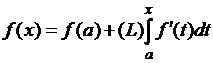 , в частности, равенство
, в частности, равенство
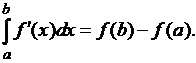
Возникает
вопрос: не лишнее ли условие 2) теоремы, т.е. само существование конечной производной
![]() не обеспечивает ли ее
суммируемость?
не обеспечивает ли ее
суммируемость?
Оказывается,
нет. Так, легко показать, что функция
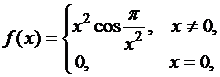
имеет конечные производные во всех
точках отрезка ![]() , но при этом производная
, но при этом производная ![]() не будет суммируемой
функцией на отрезке
не будет суммируемой
функцией на отрезке ![]() .
.
Значит,
интеграл Лебега не полностью решает задачу восстановления самой функции по ее
производной, даже если эта производная существует и конечна во всех точках
отрезка ![]() (дополнительно
требуется выполнение условия 2) из теоремы). В настоящее время построен так
называемый интеграл Перрона, который полностью решает эту задачу.
(дополнительно
требуется выполнение условия 2) из теоремы). В настоящее время построен так
называемый интеграл Перрона, который полностью решает эту задачу.
Другой
вопрос: раз в теореме производная ![]() находится под знаком
интеграла Лебега и в интегралах Лебега можно пренебречь множеством меры нуль,
нельзя ли вместо условия 1) теоремы потребовать существование конечной
производной
находится под знаком
интеграла Лебега и в интегралах Лебега можно пренебречь множеством меры нуль,
нельзя ли вместо условия 1) теоремы потребовать существование конечной
производной ![]() лишь почти всюду (а не
всюду) на отрезке
лишь почти всюду (а не
всюду) на отрезке ![]() ?
?
Ответ
отрицательный. Г. Кантор построил функцию ![]() («канторову
лестницу»), производная которой равна нулю почти всюду на отрезке
(«канторову
лестницу»), производная которой равна нулю почти всюду на отрезке ![]() (а значит,
суммируема), но не выполняется равенство
(а значит,
суммируема), но не выполняется равенство
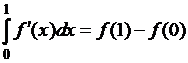 .
.
Эти особенности интеграла Лебега не
оказывают серьезного влияния на его важную роль в современном анализе.
Дело,
в частности, в том, что существует достаточно широкий класс функций, который
полностью можно охарактеризовать с помощью связи дифференцирования и
интегрирования по Лебегу. Таковым является класс абсолютно непрерывных на
данном отрезке функций.
Функция
![]() называется абсолютно непрерывной на данном отрезке
называется абсолютно непрерывной на данном отрезке ![]() , если при любом
, если при любом ![]() найдется
найдется ![]() такое, что для любой
системы неналегающих интервалов
такое, что для любой
системы неналегающих интервалов ![]() из
из
![]() с суммарной длиной
с суммарной длиной 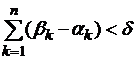 выполняется
неравенство
выполняется
неравенство 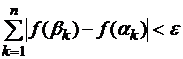 .
.
Оказывается,
для того чтобы функция ![]() была абсолютно непрерывной на данном отрезке
была абсолютно непрерывной на данном отрезке ![]() , необходимо и
достаточно, чтобы при всех
, необходимо и
достаточно, чтобы при всех ![]() выполнялось равенство
выполнялось равенство 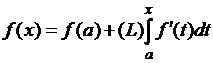 .
.
Абсолютная
непрерывность функций используется при замене
переменной и интегрировании по частям
в интегралах Лебега.
Так,
если функция ![]() суммируема на отрезке
суммируема на отрезке ![]() , функция
, функция ![]() абсолютно непрерывна
и строго возрастает, то
абсолютно непрерывна
и строго возрастает, то
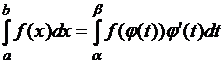 .
.
Если функции ![]() и
и ![]() абсолютно непрерывны
на отрезке
абсолютно непрерывны
на отрезке ![]() , то
, то
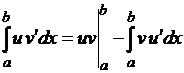 .
.
Приведем
еще одно важное свойство интеграла Лебега, благодаря которому этот интеграл
находит широкие применения в различных
областях математики.
Пусть
 - ряд Фурье
- ряд Фурье ![]() -периодической функции
-периодической функции ![]() . Требуется охарактеризовать класс
. Требуется охарактеризовать класс ![]() -периодических функций
-периодических функций ![]() , для которых выполняется равенство
Парсеваля
, для которых выполняется равенство
Парсеваля
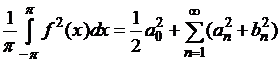
(аналог теоремы Пифагора для функций).
Оказывается, равенство Парсеваля
выполняется тогда и только тогда, когда
функция ![]() измерима на отрезке
измерима на отрезке ![]() и функция
и функция ![]() интегрируема по Лебегу
на этом отрезке.
интегрируема по Лебегу
на этом отрезке.
Наконец, приведем
замечательное свойство интеграла Лебега - теорему о предельном переходе под знаком интеграла для суммируемых функций (ср. со свойством
![]() из § 9).
из § 9).
Теорема. Если для
измеримых на множестве ![]() функций
функций ![]() (
(![]() ) существует суммируемая на
) существует суммируемая на ![]() функция
функция ![]() такая, что
такая, что ![]() (для любого
(для любого ![]() ;
; ![]() ), и существует
), и существует ![]() для почти всех
для почти всех ![]() , то выполняется равенство
, то выполняется равенство
![]() .
.
Оглавление