§11. Суммируемые неотрицательные функции

Пусть функция неотрицательна и измерима на данном ограниченном множестве и пусть - любое натуральное число. Тогда функция

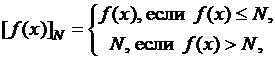называется -срезкой функции .

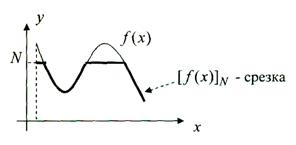
Ясно, что функция будет измеримой и ограниченной на множестве . Очевидно, ; измеримость множеств вида легко устанавливается. Поэтому при любом натуральном существует .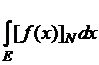

Интегралом Лебега от неотрицательной измеримой на ограниченном множестве функции называется следующий предел:

.

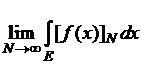Если этот предел конечен, то функция называется суммируемой или интегрируемой по Лебегу на множестве .

Ясно, что если неотрицательная функция ограничена и измерима на (ограниченном) множестве , то она будет суммируемой на этом множестве.

Действительно, так как ограничена, то ее значения будут не больше некоторого натурального числа . Поэтому при всех достаточно больших значениях на множестве выполняется тождество , а поэтому получается предел стационарной числовой последовательности:

=.

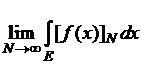Замечание. Если функция неотрицательна и измерима на неограниченном множестве , то интеграл Лебега от нее определяется в виде предела (он существует, конечный или бесконечный, как предел монотонной последовательности).

Оглавление