Тема 9. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
9.1.
Задача о вычислении криволинейной трапеции
9.2. Свойства определенного интеграла
9.3.
Вычисление определенного интеграла. Формула Ньютона-Лейбница
9.4.
Методы интегрирования определенного интеграла
9.5. Приложения определенного интеграла
9.1. Задача о вычислении площади криволинейной трапеции
Пусть на отрезке [a;b] задана
непрерывная неотрицательная функция y = f (x).
Определение 1.
Криволинейной трапецией называется фигура, ограниченная осью
абсцисс, прямыми x = a, x = b и
графиком функции y = f(x).
Ставится задача: вычислить площадь
этой криволинейной трапеции (рис. 13)
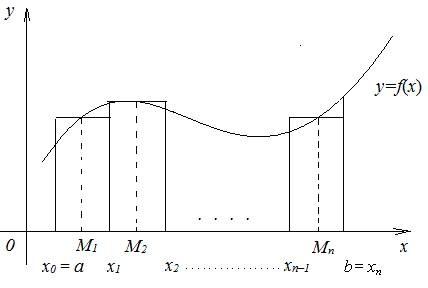
Решение.
1) Разобьём отрезок [a;b] на n частей точками x0
= a; x1; x2; xn–1; xn = b и проведём
прямые x =
x1, x = x2, … x = xт–1, которые разобьют трапецию на n частей.
2) Обозначим Dxk = xk – xk–1
– длины отрезков разбиения [a;b]. На каждом из отрезков произвольно
выберем точку Mk (k = 1, 2,…, n).
Построим на каждом из отрезков прямоугольники с высотами,
равными значению функции в выбранных точках Mk
.
Площади полученных прямоугольников равны:
S1 = f (M1) × D x1; S2 = f (M2) × D x2, …., Sn =
f (Mn)
× D xn .
3) Найдём сумму этих площадей:
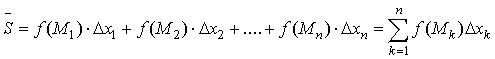
Получили площадь ступенчатой фигуры. Эта
площадь зависит от способа разбиения отрезка [a;b] на части и
от выбора на каждой из частей точек Mk (k = 1, 2,…, n).
Чем больше будет точек разбиения
отрезка [a;b] на части и мельче по длине эти
части, тем точнее сумма 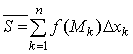 будет приближаться к
площади данной криволинейной трапеции, т.е. можно записать:
будет приближаться к
площади данной криволинейной трапеции, т.е. можно записать:
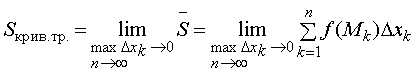
Определение 2. Сумма  называется
интегральной суммой функции f (x) на отрезке [a;b].
называется
интегральной суммой функции f (x) на отрезке [a;b].
Определение 3. Предел интегральной суммы ![]() функции f (x) на отрезке
[a;b] при n ® ¥ и max Dxk ® 0
называется определённым интегралом
функции f (x) на отрезке [a;b], если этот предел существует и не зависит ни от
способа разбиения отрезка [a;b] на части, ни от выбора точек Mk (k = 1,…, n) на каждой из частей. Следовательно, можно записать:
функции f (x) на отрезке
[a;b] при n ® ¥ и max Dxk ® 0
называется определённым интегралом
функции f (x) на отрезке [a;b], если этот предел существует и не зависит ни от
способа разбиения отрезка [a;b] на части, ни от выбора точек Mk (k = 1,…, n) на каждой из частей. Следовательно, можно записать:
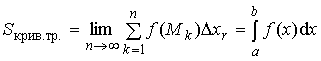 .
.
При этом отрезок [a;b] называют отрезком интегрирования, “a” –
нижним пределом интегрирования, “b” – верхним пределом.
Теорема 1 (достаточное условие
интегрируемости функции на отрезке [a;b]). Если функция f(x) на отрезке [a;b] непрерывна, то определённый интеграл  существует, т.е.
функция f (x) на отрезке [a;b]
интегрируема.
существует, т.е.
функция f (x) на отрезке [a;b]
интегрируема.
Геометрический смысл определённого интеграла
1) 

2) Если область ограничена двумя
кривыми y =
f (x) и y = g(x), причём при
xÎ [a;b] f (x) ³ g(x), то площадь области, ограниченной
кривыми y = f (x); y = g(x) и прямыми x = a,
x = b, вычисляется по формуле:
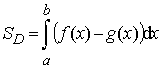

9.2. Свойства определённого интеграла
1) 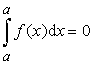
2) 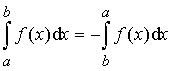
3) 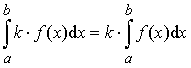
4) 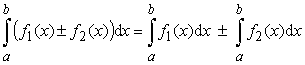
5) Если функция f(x) интегрируема на отрезках [a;c] и [c;b], то она интегрируема и на отрезке [a;b], причём верно равенство:
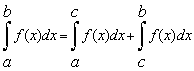
при любом расположении точек a, b и c на оси Ox.
6) Если f (x) ³ 0 при xÎ [a;b], то
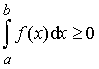
7) Если на отрезке [a;b] f (x) ³ g (x), то

8) Теорема 2 (о среднем значении
определённого интеграла). Если функция
f (x) непрерывна на отрезке [a;b], то на
этом отрезке найдётся хотя бы одна точка c, в которой
выполняется равенство:

Доказательство. Так как
функция f(x) на
отрезке [a;b] непрерывна,
то она достигает на этом отрезке своих наименьшего “m” и
наибольшего “M” значений. Тогда
m £ f(x) £ M для любого xÎ[a;b]. По
свойству 7 определённого интеграла можно записать неравенство:
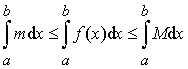
Так как m и M –
постоянные числа, то
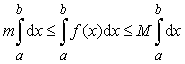 (*)
(*)
Вычислим по определению определённого интеграла
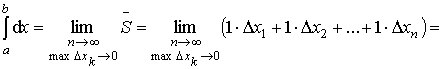
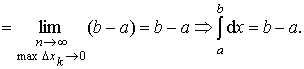
Тогда неравенство (*) можно переписать в виде:
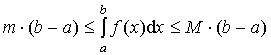 .
.
Разделим все части полученного
неравенства на (b – a) > 0 (длина отрезка
интегрирования):
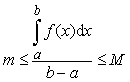
Так как функция f(x) непрерывна на отрезке [a;b], то она принимает все значения, заключённые между
наименьшим “m” и наибольшим “M” значениями. Значит найдётся на отрезке [a;b] хотя бы одна точка c, в которой
выполняется равенство:
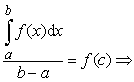
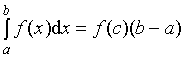 .
.
Теорема доказана.
9.3. Вычисление определенного интеграла. Формула Ньютона–Лейбница
Интеграл с переменным верхним пределом
и его свойства
Определение 4. Пусть функция y = f(x) непрерывна на отрезке [a;b]. Тогда она
непрерывна на отрезке [a;x] для любого xÎ[a;b].
Следовательно, на отрезке [a;b] определена функция 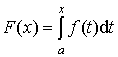 , которая называется интегралом
с переменным верхним пределом.
, которая называется интегралом
с переменным верхним пределом.
Свойства этой функции сформулируем в виде теоремы.
Теорема 3. Пусть функция f(x) непрерывна на отрезке [a;b]. Тогда функция
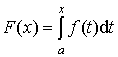 обладает свойствами:
обладает свойствами:
1) непрерывна на отрезке [a;b];
2) имеет производную F'(x) в каждой
точке xÎ[a;b],
удовлетворяющую равенству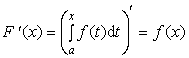 .
.
Доказательство.
Вычислим приращение функции F(x), причём Dx возьмём таким, чтобы точка x + Dx Î [a;b].
Тогда
![]()
![]()
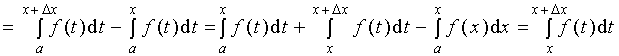 .
.
Применим к полученному интегралу
теорему о среднем значении определённого
интеграла, т.е. на отрезке [x;
x +
Dx] существует такое число c, в котором
выполняется равенство:
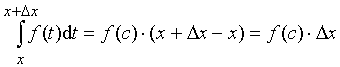
Значит, DF = f (c)× Dx, где c Î [x; x + Dx].
Если Dx ® 0, то c ® x (так как x < c < x + Dx).
Поэтому, в силу непрерывности f (x), получим f (c) ® f (x) при Dx®0.
Таким образом, DF®0 при Dx®0, что доказывает непрерывность F(x).
Кроме того, вычисляя предел отношения
DF к Dx при Dx ® 0, получим:
 ,
,
т.е. существует конечный предел
отношения DF к Dx при Dx ® 0, что означает существование
производной F' (x) = f (x).
Теорема доказана.
Из теоремы 3 следует, что функция 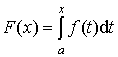 является первообразной
для функции f (x).
является первообразной
для функции f (x).
Формула Ньютона–Лейбница
Теорема 4. Пусть функция
f (x) непрерывна на отрезке [a;b] и F(x) – какая-либо её первообразная на отрезке [a;b]. Тогда определённый интеграл от функции f(x) по отрезку [a;b] равен разности значений функции F(x) в точках b и a:
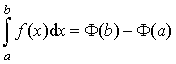
Доказательство.
Из теоремы 3 следует, что наряду с функцией F(x) функция 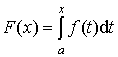 также является на отрезке [a;b]
первообразной для f(x). Тогда по свойству
первообразных для одной и той же функции на некоторой области имеем:
также является на отрезке [a;b]
первообразной для f(x). Тогда по свойству
первообразных для одной и той же функции на некоторой области имеем:
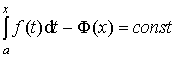 для любого xÎ [a;b] (**)
для любого xÎ [a;b] (**)
Вычислим значение const. Для этого, используя свойство 1
определённого интеграла (§3, п.2, с. 93) 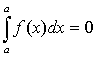 , рассмотрим равенство (**) при x = a:
, рассмотрим равенство (**) при x = a:
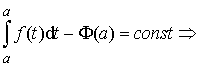
![]()
Следовательно, равенство (**) можно переписать в виде:
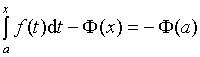 для xÎ [a;b]
для xÎ [a;b]
Теперь рассмотрим полученное равенство при x = b:
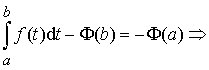
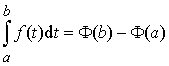
Это и есть формула Ньютона–Лейбница. Она является основной формулой
интегрального исчисления, устанавливающей связь между определённым и неопределённым
интегралами, и даёт правило вычисления определённого интеграла.
Замечание.
Формулу Ньютона–Лейбница часто записывают в виде:
 ,
,
где используется обозначение:
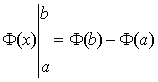 .
.
Задача вычисления определённого интеграла
свелась к нахождению первообразной
непрерывной функции.
Пример 1. Вычислить
интеграл:
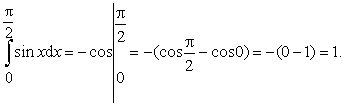
![]()
Ответ: 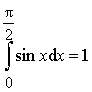 .
.
Пример 2. Вычислить интеграл:
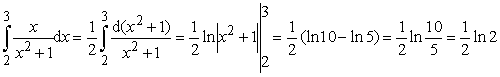 .
.
Ответ:  .
.
9.4. Методы интегрирования определённого интеграла
Замена переменной в
определённом интеграле
Теорема 5. Пусть функция f(x) непрерывна на отрезке [a;b] и пусть функция
x = j(t) имеет
непрерывную производную j'(t) на отрезке
[a;b], область значений этой функции –
отрезок [a;b], т.е. a £ j (t) £ b для tÎ [a;b], причём j(a) = a, j(b) = b.
Тогда справедливо равенство:
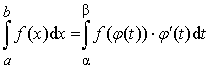 .
.
Доказательство.
Так как функция f(x) непрерывна
на отрезке [a;b], то существует определённый
интеграл 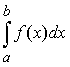 и справедлива формула
Ньютона– Лейбница:
и справедлива формула
Ньютона– Лейбница:
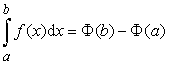 (1)
(1)
где F(x) – одна из
первообразных f (x) на отрезке [a;b].
Известно, что F(x) дифференцируема в любой точке отрезка [a;b], причём
F'(x) = f (x) для любого xÎ [a;b].
Так как функция x = j(t) непрерывна
на [a;b] и множество её значений совпадает с
отрезком [a;b], то сложные функции f(j(t)) и F(j(t)) непрерывны в любой точке t Î [a;b].
Так как j'(t) непрерывна на отрезке [a;b], то функция f(j(t)) × j'(t) тоже непрерывна на [a;b], а значит существует интеграл:
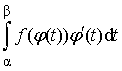 .
.
Покажем, что функция F(j(t)) является первообразной для ![]() . Действительно, (F(j (t)))'t = F'(x)× j'(t) = f (x)× j'(t) = f
(j (t))× j'(t) для любого t Î [a;b]. Поэтому можно к этому интегралу
применить формулу Ньютона–Лейбница:
. Действительно, (F(j (t)))'t = F'(x)× j'(t) = f (x)× j'(t) = f
(j (t))× j'(t) для любого t Î [a;b]. Поэтому можно к этому интегралу
применить формулу Ньютона–Лейбница:
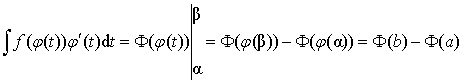 (2)
(2)
(так как j(b)
= b и j(a) = a).
Сравнивая результаты (1) и (2)
приходим к равенству:
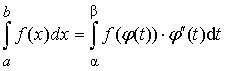 .
.
Пример 3. Вычислить
интеграл:
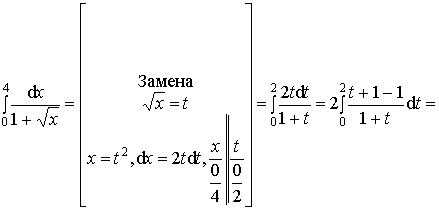
 .
.
Ответ: 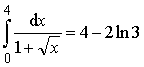 .
.
Пример 4.
Вычислить интеграл:
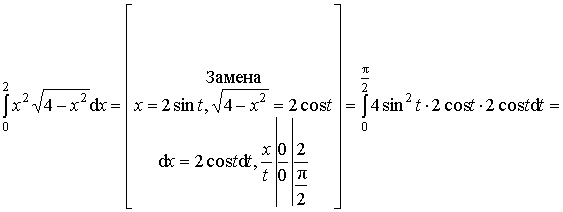
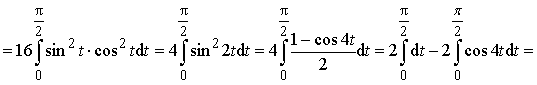

Ответ: 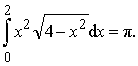
Интегрирование по частям в
определённом интеграле
Теорема 6. Пусть функции u(x)
и v(x) имеют непрерывные производные на отрезке [a;b]. Тогда справедливо равенство:
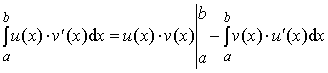 .
.
Доказательство. Так как (u(x)× v(x))' = u(x)
v' (x) + u' (x)× v(x) для
любого x Î [a;b], то функция u(x) × V(x) является одной
из первообразных функции u (x) ∙ v' (x) + u' (x) ∙ v(x).
Поэтому по формуле Ньютона–Лейбница:
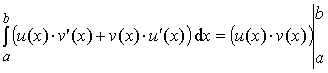
Пользуясь свойством определённого
интеграла можно это равенство записать в виде:
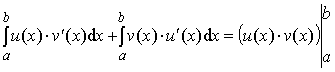
Отсюда следует:
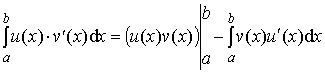
Эту формулу удобно записать в виде:
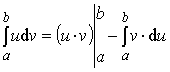
Пример 5. Вычислить интеграл:
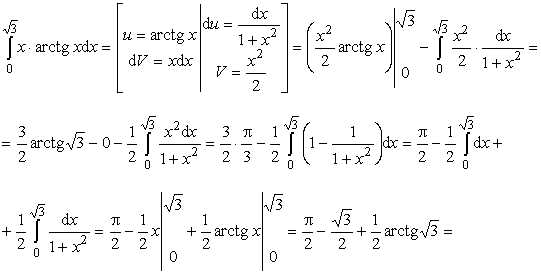
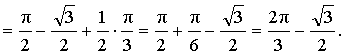
Ответ: 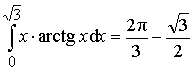 .
.
Пример 6. Вычислить
интеграл:

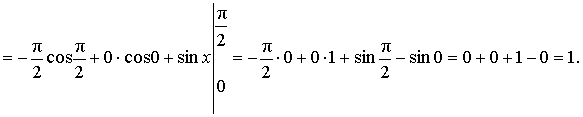
Ответ: 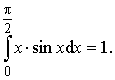
9.5. Приложения определённого интеграла
Вычисление площадей плоских фигур в
прямоугольной системе координат
а) Область D ограничена
кривыми y = f(x) и y = g(x), прямыми x =
a и
x =
b, причём f(x) ³ g(x) для
xÎ[a;b].
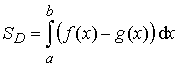 .
.
б) Область D ограничена кривыми x = f(y) и x = g(y), прямыми y =
c и y = d, причём f (y) ³ g(y) для yÎ[c;d].
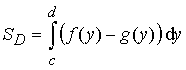 .
.
Вычисление площади плоской фигуры в
полярной системе координат
а) Полярная система координат задается полярной осью Ox, полюсом – точка O и
масштабной единицей (рис. 14)
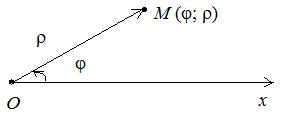
Точка M в этой системе задаётся двумя
координатами (j и r): j – угол наклона радиуса-вектора ![]() к оси Ox; r – длина радиуса-вектора
к оси Ox; r – длина радиуса-вектора ![]() . Формулы перехода от полярной системы координат к
прямоугольной системе, связанной с полярной точкой начала координат – точка 0, осью абсцисс с полярной осью и осью
ординат, перпендикулярной полярной оси
. Формулы перехода от полярной системы координат к
прямоугольной системе, связанной с полярной точкой начала координат – точка 0, осью абсцисс с полярной осью и осью
ординат, перпендикулярной полярной оси
M(j;r) = M(x; y): 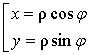 и
и 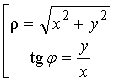
Уравнение кривой в полярной системе координат – соотношение
между r и j:
r = r (j).
б) Площадь криволинейного сектора в полярной системе,
ограниченного лучами j =a и j = b, кривой r = r(j) (рис. 15),
вычисляется по формуле:
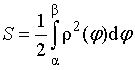 .
.
Вычисление объёма тела по площадям
параллельных сечений
Пусть задано объёмное тело T, для
которого известна площадь S(x) любого
сечения плоскостью, проходящей через точку (x;0;0) перпендикулярно
оси Ox, a £ x £ b (рис. 16).
Нужно вычислить объём тела.
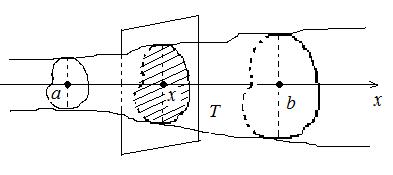
Пусть функция S(x) непрерывна
на отрезке [a;b]. Тогда
объём тела T вычисляется по формуле:
 .
.
Вычисление объёма тела вращения
Надо вычислить объём тела, образованного
вращением вокруг оси Ox криволинейной трапеции ABCD, ограниченной кривой y = f (x), осью Ox и прямыми x =
a, x = b.
В таком случае площадь поперечного
сечения в точке xÎ [a;b] круг радиусом f(x) равна:
![]() .
.
Тогда объём тела, образованного
вращением вокруг оси Ox криволинейной трапеции ABCD, вычисляется по формуле:
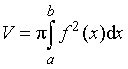 .
.
Объём тела, образованного вращением
вокруг оси Oy криволинейной трапеции ABCD, ограниченной кривой x = j(y), осью Oy и прямыми y = c,
y = d,
вычисляется по формуле:
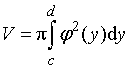 .
.