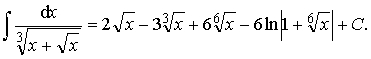Тема 8. МЕТОДЫ ИНТЕГРИРОВАНИЯ
8.1. Непосредственное интегрирование
8.2. Интегрирование подстановкой
8.4. Интегрирование рациональных функций
8.5. Интегрирование тригонометрических функций
8.6. Интегрирование некоторых иррациональных выражений
8.1. Непосредственное интегрирование
а) Применение таблицы: предложенный интеграл оказался одним из
табличных интегралов. В этом случае требуется безошибочно найти соответствующую
формулу таблицы основных интегралов и ею воспользоваться.
Пример 1.
1. 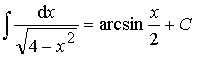 (формула 14)
(формула 14)
2. 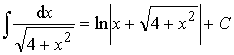 (формула 16)
(формула 16)
б) Метод разложения: предложенный
интеграл после применения линейных свойств (4 и 5) неопределённого интеграла заменяется на алгебраическую сумму табличных интегралов.
Пример 2.

Ответ: 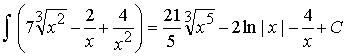 .
.
Пример 3.


Ответ: ![]() .
.
Пример 4.
![]()
Ответ: ![]()
в) Подведение под знак дифференциала: предложенный интеграл удается
свести к табличному с помощью изменения переменой
интегрирования или за счёт преобразований под знаком дифференциала. При этом
используют следующие формулы:
d(j(x)) = j'(x)dx;
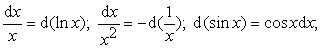
![]()
![]() и т.д.
и т.д.
Далее используют тот факт, что если
известен результат
![]() ,
,
то равенство
![]()
будет справедливо для любой
дифференцируемой функции u = j(x).
Пример 5.
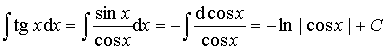
Ответ: ![]() .
.
Пример 6.
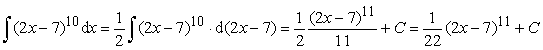 .
.
Ответ: ![]() .
.
Пример 7.
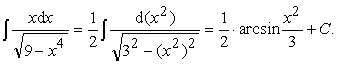
Ответ: 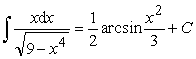 .
.
Пример 8.
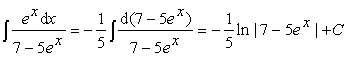 .
.
Ответ: 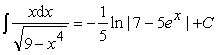 .
.
Пример 9.
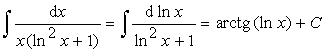 .
.
Ответ: 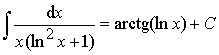 .
.
8.2. Интегрирование подстановкой
Подстановка (или замена переменной)
базируется на следующей теореме.
Теорема 1. Если не удаётся найти интеграл ![]() непосредственно, то
можно выбрать такую функцию x =
j(t), удовлетворяющую условиям:
непосредственно, то
можно выбрать такую функцию x =
j(t), удовлетворяющую условиям:
1) j(t) непрерывна при t Î (a;b), соответствующем интервалу xÎ (a;b),
2) дифференцируемая при tÎ (a;b);
3) имеет обратную функцию t = j–1(x),
чтобы ![]() , t =
j–1(x), стал
табличным или более простым. Иногда для упрощения интеграла можно сделать
замену t = y(x).
, t =
j–1(x), стал
табличным или более простым. Иногда для упрощения интеграла можно сделать
замену t = y(x).
Замечание.
Выбор правильной подстановки в значительной степени зависит от искусства
вычисляющего.
Пример 10.
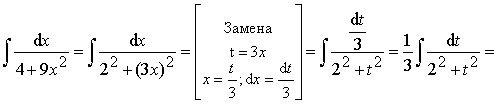
![]() .
.
Ответ: 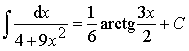 .
.
Пример 11.
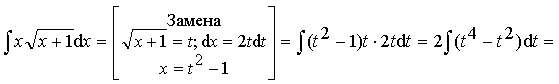
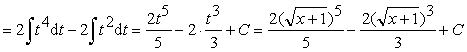 .
.
Ответ: ![]() .
.
Пример 12.
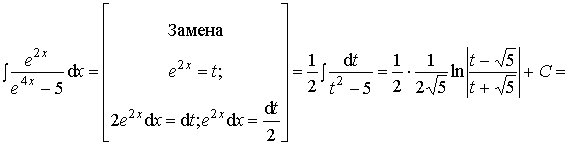
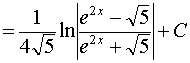 .
.
Ответ: 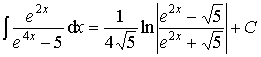 .
.
Пример 13. 
![]()
![]()
![]()
 .
.
Ответ:
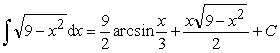 .
.
8.3. Интегрирование по частям
Метод
интегрирования по частям базируется на следующей теореме.
Теорема 2. Пусть функции u = u(x) и v = v(x)
дифференцируемы на некотором интервале (a;b). Пусть на интервале (a;b) функция v(x)×u'(x) имеет первообразную.
Тогда на интервале (a;b) функция u(x)×v'(x) также имеет первообразную.
При этом справедливо равенство:
![]() .
.
Доказательство.
По формуле дифференцирования произведения:
(u(x)×v(x))'= u '(x)×v(x) + u(x)×v '(x)
и свойству неопределённого интеграла:
![]()
можно записать:
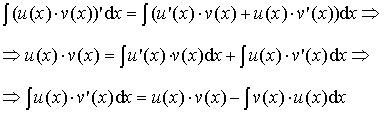
Замечание 1.
Определение дифференциала и свойства инвариантности его формы позволяют
переписать формулу интегрирования по частям в более короткой форме:
![]() .
.
Замечание 2.
Для успешного вычисления интеграла необходимо разумно разбить подынтегральное
выражение на два множителя u(x) и dv(x) так, чтобы
интеграл ![]() оказался легко
интегрируемым.
оказался легко
интегрируемым.
Практика показывает, что большая
часть интегралов, берущихся с помощью метода интегрирования по частям, может
быть разбита на следующие три группы.
1)
К первой группе относятся
интегралы, у которых подынтегральная функция содержит в качестве множителя одну
из следующих функций:
ln x; arcsin
x;
arccos x; arctg x;
arcctg x; ln2x; lnj(x);
arcsin2x;…
при условии, что оставшаяся часть
подынтегральной функции представляет собой производную известной функции.
Тогда за функцию u(x) берут соответствующую из перечисленных.
2) Ко второй группе относятся интегралы вида:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
где a,b,a,n,A – некоторые постоянные числа, A >
0, n Î N.
При этом в качестве u(x) следует брать (ax +b)n и интегрировать по частям n раз.
3) К третьей группе относятся
интегралы вида:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
где a, b, A – постоянные числа, A > 0, A ≠ 1.
Такие интегралы берутся двукратным
интегрированием по частям при любом выборе u(x). Это приводит к линейному уравнению относительно
предложенного интеграла, откуда его и находят.
Замечание. Указанные
три группы не исчерпывают всех без исключения интегралов, берущихся методом
интегрирования по частям.
Пример 14.
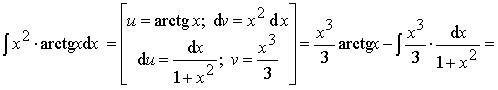
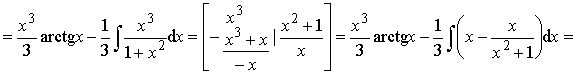
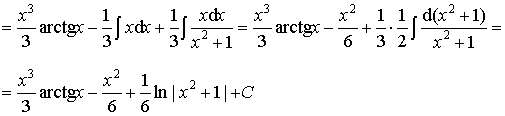
Ответ: 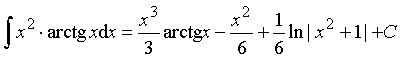
Пример 15.
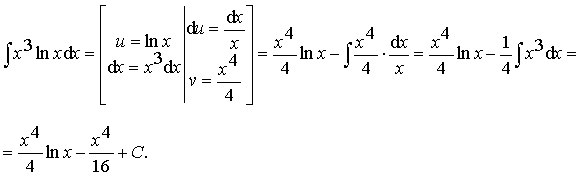
Ответ: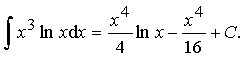
Пример 16.
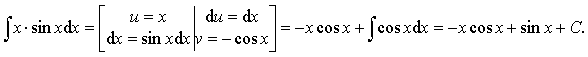
Ответ: ![]()
Пример 17.
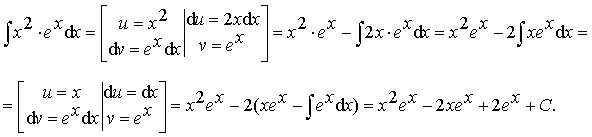
Ответ:![]()
Пример 18.
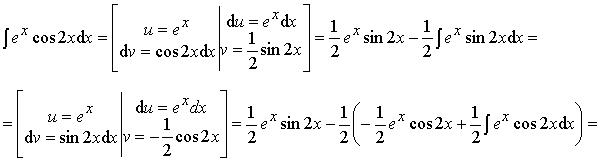
![]()
Далее необходимо решить уравнение:
![]()
Пусть![]() , тогда уравнение запишется в виде:
, тогда уравнение запишется в виде:
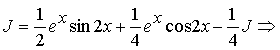
![]()
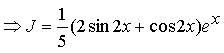 .
.
Ответ: ![]()
 .
.
8.4. Интегрирование рациональных дробей
Разложение рациональной дроби на
сумму простых дробей
Определение 1. Рациональной
дробью называется отношение двух многочленов:
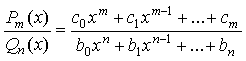
![]()
![]()
Определение 2. Рациональная дробь называется правильной, если m < n. В противном случае (если m ³ n) она называется неправильной.
Определение 3. Простыми
рациональными дробями называются дроби следующих четырех типов:
I .  ,
,
II. 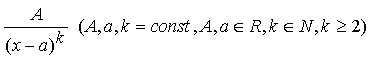 ,
,
III. 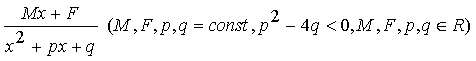 ,
,
IV.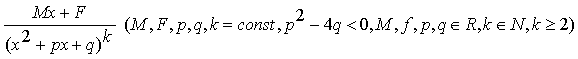
Теорема 3. Всякую неправильную рациональную
дробь можно представить в виде суммы целой части (многочлена) и правильной
рациональной дроби.
Пример 20.
Представить дробь 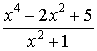 в виде суммы целой
части и правильной рациональной дроби.
в виде суммы целой
части и правильной рациональной дроби.
Так как высшая степень числителя
равна 4, а знаменателя – 2, то данная дробь неправильная (4 > 2). Разделим
числитель на знаменатель:
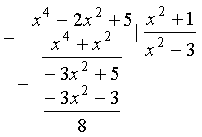
Следовательно, дробь можно записать в виде:
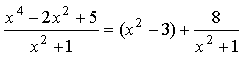 .
.
Ответ: ![]()
 .
.
Теорема 4. Любую правильную рациональную дробь
можно единственным образом представить в виде суммы конечного числа простых
рациональных дробей.
Разложение правильной рациональной
дроби 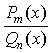 (m<n) на сумму простых дробей можно выполнить по следующей
схеме:
(m<n) на сумму простых дробей можно выполнить по следующей
схеме:
·
Найти
корни многочлена Qn(x) и представить его в виде произведения простых
множителей:
![]() ,
,
где ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
·
Записать
разложение дроби с неопределёнными коэффициентами:
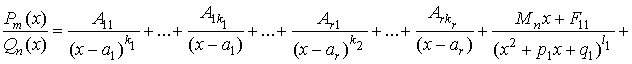
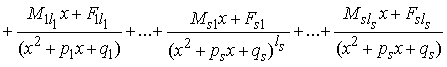
·
Определить
коэффициенты
![]()
суммарное число
которых равно n, методом неопределенных
коэффициентов.
Для этого необходимо всё разложение
привести к общему знаменателю и приравнять числитель полученной дроби к Pm(x).
Приравнивая в этих многочленах коэффициенты при одинаковых степенях x, получим систему из n линейных
уравнений с n неизвестными. Эта система имеет
единственное решение – искомые коэффициенты.
Пример 21.
Разложить дробь 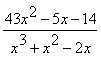 на сумму простых
дробей.
на сумму простых
дробей.
1) Данная дробь правильная. Разложим
знаменатель на множители:
![]() .
.
2) Запишем разложение данной дроби на сумму простых дробей:

3) Для нахождения коэффициентов A, B и
C приводим разложение дроби к общему
знаменателю и приравняем числители дробей.
![]()
![]()
![]()
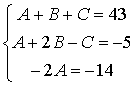
![]()
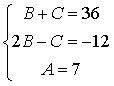
![]()
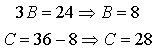
Следовательно, дробь можно
записать в виде:
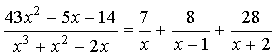 .
.
Ответ: 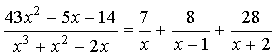 .
.
Интегрирование простых дробей
Задача интегрирования рациональной
дроби сводится к умению интегрирования только правильных рациональных дробей,
так как интегрирование целой части дроби (многочлена) – задача не сложная. Если
решена задача разложения правильной дроби на сумму простых дробей, то дальше
надо уметь интегрировать простые дроби. Покажем, как интегрировать простые
дроби (четыре типа).
I тип. ![]()
II тип. 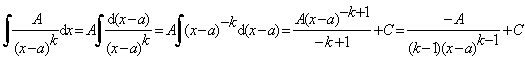
![]()
III тип. 
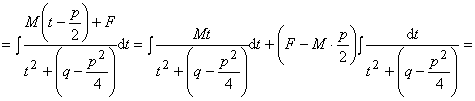

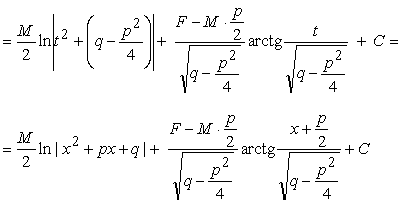
Интегрирование дроби IV типа проводится аналогично
интегрированию дроби III типа.
Пример 22. Найти интеграл от дроби III типа:
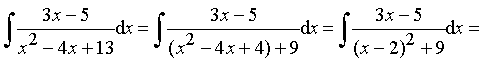
(D = 16 – 52 < 0 Þ дробь III типа)

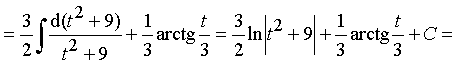
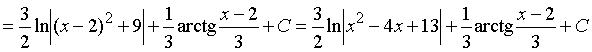 .
.
Ответ: 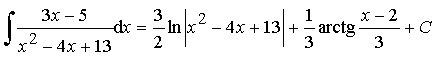 .
.
Пример 23. Найти интеграл от дроби IV типа:
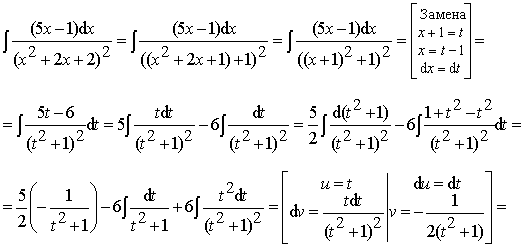
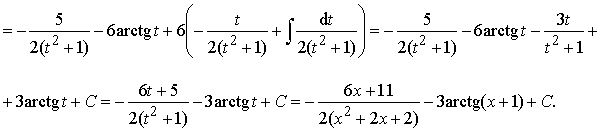
Ответ: 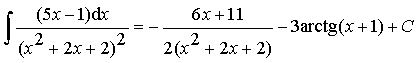 .
.
Итак, любая рациональная дробь
интегрируема. Для этого необходимо выполнить следующие шаги:
1) Выделить целую часть дроби, если
дробь является неправильной, т.е. представить в виде:
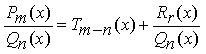 ,
,
где Tm–n(x) и Rr(x) – многочлены
степени m–n и r соответственно (причём r < n).
2) Разложить правильную рациональную
дробь ![]() на сумму простых
дробей.
на сумму простых
дробей.
3) Вычислить интегралы от многочлена Tm–n(x) и каждой
из простых дробей, полученных на шаге 2).
Пример 24. Найти интеграл 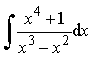
1) Дробь  – неправильная
рациональная дробь. Выделим её целую часть:
– неправильная
рациональная дробь. Выделим её целую часть:
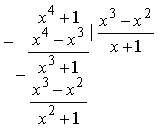
Поэтому можно записать:
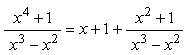 .
.
2) Полученную правильную дробь  разложим на сумму
простых дробей:
разложим на сумму
простых дробей:
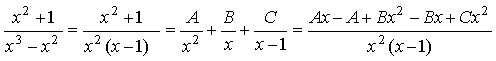
![]()
![]()

![]()
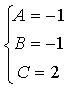
Отсюда следует: ![]()
 .
.
Значит, подынтегральную рациональную
дробь можем представить в виде:
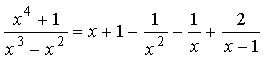 .
.
3) Найдём интеграл:

Ответ: 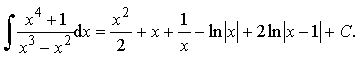
8.5. Интегрирование тригонометрических выражений
1) Интеграл вида ![]()
![]()
а) Если n – чётное
число и m – чётное, то подынтегральное
выражение преобразуют с помощью формул:
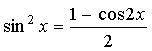 ,
, ![]()
б) Если одно из чисел m или n – нечётное, то выполняют замену:
t = sin x, если n – нечётное;
t = cos x, если m – нечётное.
Эта замена приводит к интегрированию
степенных интегралов или рациональных дробей.
в) Если оба числа m и n – нечётные, то интеграл берется как
в случае замены:
t = sin x, так и t =
cos x.
Пример 25. Вычислить интеграл:
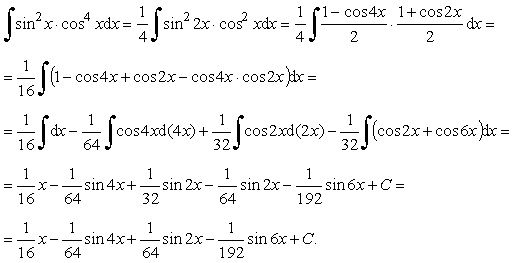
![]()
Ответ: ![]()
Пример 26. Вычислить интеграл:
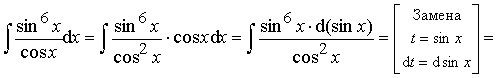

Ответ: 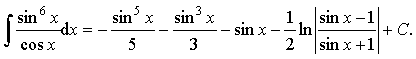
Пример 27. Вычислить интеграл:

Ответ: 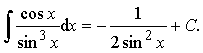
2)
Интегралы вида:
![]() ;
; ![]()
![]() ;
; ![]()
где ![]()
Такие интегралы находят после
предварительного применения формул:
![]()
![]()
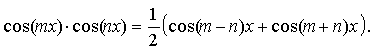
Пример 28. Вычислить интеграл:
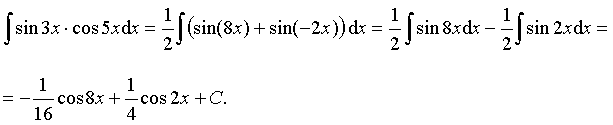
Ответ: 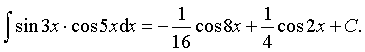
3) Интеграл вида: ![]() ,
где f(u;v) –
рациональная функция двух переменных.
,
где f(u;v) –
рациональная функция двух переменных.
Такие интегралы приводятся к интегралам
от рациональной дроби с помощью замены:
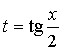 ;
;
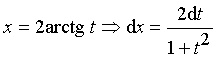 ;
;
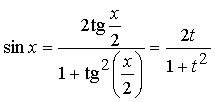 ;
;  .
.
Пример 29. Вычислить интеграл:
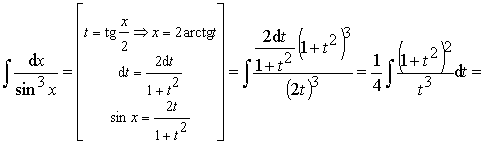
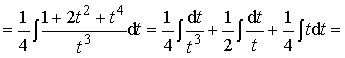
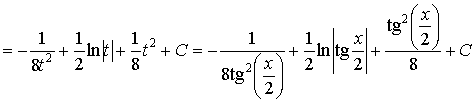 .
.
Ответ: 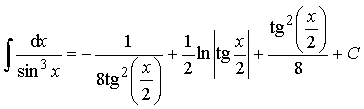 .
.
4) Интегралы вида: ![]() , где f(u;v) –
рациональная функция двух переменных.
, где f(u;v) –
рациональная функция двух переменных.
Такие интегралы находят сведением к интегралу от рациональной
дроби с помощью замены:
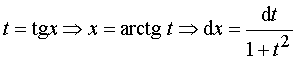
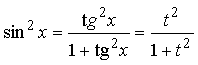 ;
; 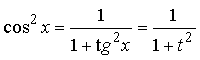
Пример 30. Вычислить интеграл:
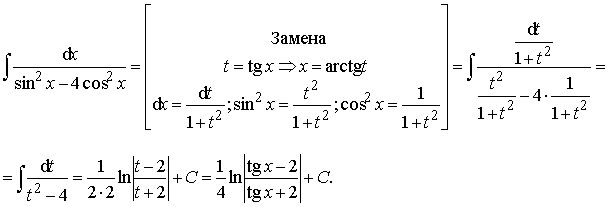
Ответ: 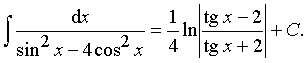
5) Интегралы вида: ![]() ;
; ![]() , где
, где ![]() .
.
Такие интегралы находят после предварительного
применения формул:
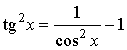 ;
; ![]()
или с помощью замены:
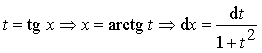 ;
;
или 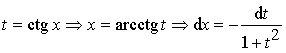 .
.
Пример 31. Вычислить интеграл:
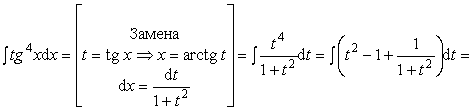
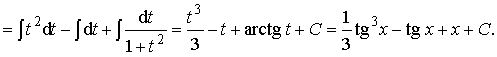
Ответ: ![]()
8.6. Интегрирование некоторых видов иррациональных выражений
1) Интеграл вида 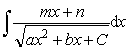
Такие интегралы находят с помощью
преобразований и замены, аналогичных преобразованиям и замене для нахождения интеграла
от простой рациональной дроби III типа.
Пример 32. Вычислить
интеграл:
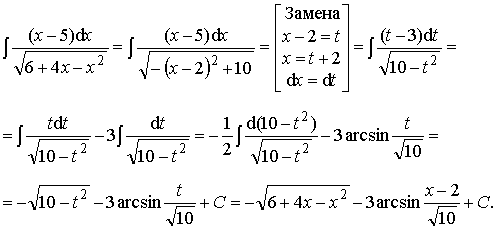
Ответ: 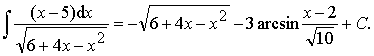
2) Подынтегральная функция содержит ![]() .
.
Тогда надо выполнить замену: 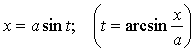 ,
, ![]() ,
, ![]() .
.
Такая
замена приводит к интегралу от некоторого тригонометрического выражения.
Пример 33. Вычислить интеграл:

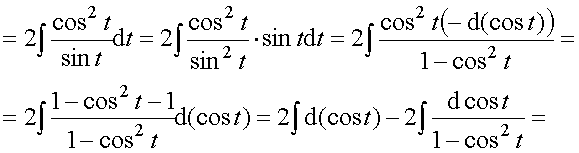

Ответ: 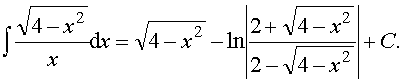
3) Подынтегральная
функция содержит ![]() .
.
Тогда надо выполнить замену:
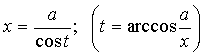
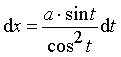
![]()
Пример 34. Вычислить интеграл:
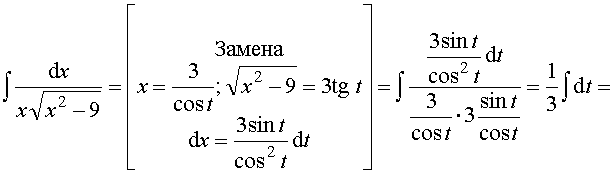

Ответ: 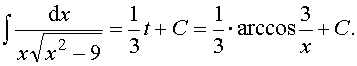
4) Подынтегральная
функция содержит ![]() .
.
Тогда надо выполнить замену: 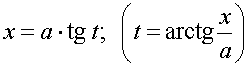 ,
, 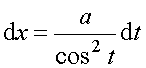 ,
, 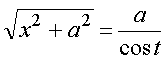 .
.
Пример 35. Вычислить интеграл:
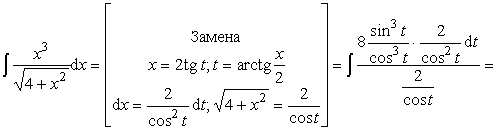
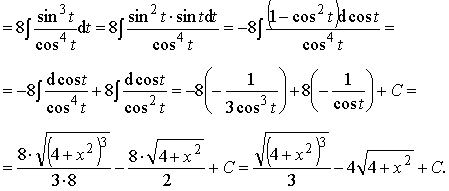
Ответ: 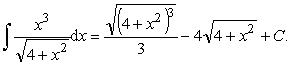
5) Подынтегральная
функция содержит ![]() :
:
Тогда надо выполнить замену:
![]() .
.
Пример 36. Вычислить интеграл:
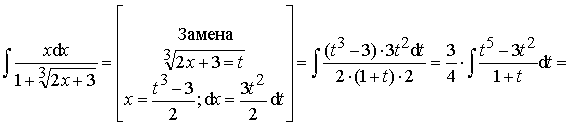
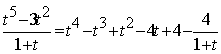
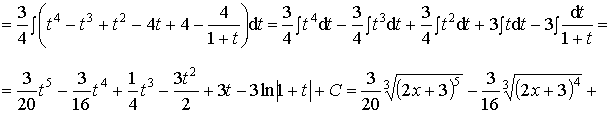
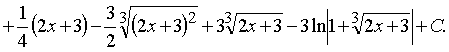
Ответ: 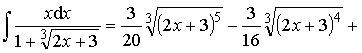
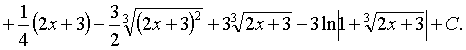
![]()
![]()
![]()
Пример 37. Вычислить интеграл:
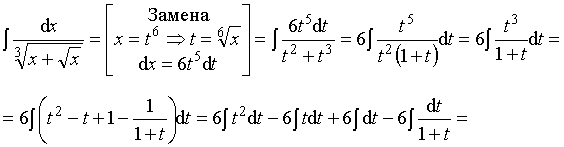
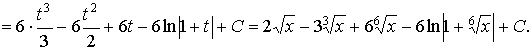
Ответ: