Тема 7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
7.1. Первообразная функция и ее свойства
7.2. Понятие неопределенного интеграла
7.3. Свойства неопределенного интеграла
7.4. Таблица неопределенных интегралов
7.1. Первообразная функция и её свойства
Определение 1. Функция F(x) называется
первообразной для функции f(x) на некотором промежутке, если в
каждой точке этого промежутка функция F(x) дифференцируема и выполняется равенство F '(x) =
f(x).
Пример 1.
Функция F (x) = sin x
является первообразной функции f(x) = cos x на бесконечном промежутке (– ¥;
+¥),
так как
F’(x) = (sin x) ‘ =
cos x
= f(x) для x Î
(– ¥;+¥).
Нетрудно убедиться, что функции F1(x) = sin x + 5 и F2(x) = sin x – 10 также являются
первообразными функции f(x) = cos x для всех 
(– ¥;+¥), т.е. если для функции f(x) на некотором промежутке существует
первообразная функции, то она не является единственной. Докажем, что множество
всех первообразных для данной функции f(x) есть множество, которое задаётся формулой F(x) + C, где C – любая постоянная величина.
Теорема 1 (об общем виде первообразной). Пусть F(x) – одна из
первообразных для функции f(x) на
интервале (a;b). Тогда
любая другая первообразная для функции f(x) на интервале (a;b) представлена в виде
F(x) + C, где C –
некоторое число.
Доказательство.
Во-первых, проверим, что F(x) + C также является первообразной для
функции f(x) на
интервале (a;b).
По условию теоремы F(x) на интервале (a;b) является первообразной для функции f(x), поэтому выполняется равенство:
F '(x) = f(x) при любом xÎ (a;b).
Так как С
– некоторое число, то
(F(x) + С) ' = F '(x)+С ' = F '(x) + 0 = f(x).
Отсюда следует: (F(x) + С)' = f(x) при любом xÎ (a;b), а значит F(x) + С на интервале (a;b) является первообразной для функции f(x).
Во-вторых, проверим, что если F(x) и Ф(x) – две
первообразные для функции f(x) на
интервале (a;b), то они
различаются между собой на постоянную величину, т.е. F(x) – Ф(x) = const.
Обозначим j(x) = F(x) – Ф(x). Так как по предположению функции F(x) и Ф(x) первообразные на интервале (a;b) для функции f(x), то выполняются равенства: F '(x) = f(x) и Ф'(x) = f(x) при любом xÎ (a;b).
Следовательно, j'(x) = F '(x) – Ф' (x) = f(x) – f(x) = 0 при любом xÎ (a;b).
Функция j(x) непрерывна и дифференцируема при xÎ (a;b). Значит, на любом отрезке [x1; x2] Ì (a; b) функция j(x)
удовлетворяет теореме Лагранжа: существует точка 
Î(x1; x2), для которой выполняется равенство:
j(x2)
– j(x1) = j’ ()× (x2 – x1) = 0×(x2 – x1) = 0
Þ j(x2) – j(x1)
= 0 Þ j(x2)
= j(x1) Þ j(x) = const.
Значит, F(x) – Ф(x) = const.
Итак, получили, что если известна
одна первообразная F(x) для
функции f(x) на
интервале (a;b), то любая другая
первообразная может быть представлена в виде F(x) + С, где С – произвольная постоянная величина. Такая форма
записи первообразных носит название общего
вида первообразной.
7.2. Понятие неопределённого интеграла
Определение 2. Множество всех первообразных для данной функции f(x) на интервале (a;b) называется неопределённым интегралом функции f(x) на этом интервале и обозначается символом:
В обозначении 
знак 
называется знаком интеграла,
– подынтегральным выражением, 
– подынтегральной функцией, 
– переменной интегрирования.
Теорема 2. Если функция f(x) непрерывна
на промежутке (a;b), то она
имеет на промежутке (a;b) первообразную и неопределённый интеграл.
Замечание.
Операция нахождения неопределённого интеграла от данной функции f(x) на некотором промежутке носит
название интегрирования функции f(x).
7.3. Свойства неопределённого интеграла
Из определений
первообразной F(x) и
неопределённого интеграла от данной функции f(x) на некотором промежутке следуют свойства
неопределённого интеграла:
1. 
.
2. 
.
3. 
, где С
– произвольная постоянная.
4. 
, где k = const.
5.
Замечание. Все
вышеперечисленные свойства верны при условии, что интегралы, фигурирующие в
них, рассматриваются на одном и том же промежутке и существуют.
7.4. Таблица основных неопределённых интегралов
Действие интегрирования является
обратным действию дифференцирования, т.е. по заданной производной функции f(x) надо восстановить начальную функцию
F(x). Тогда из
определения 2 и таблицы производных получается таблица основных интегралов.
1. 
.
2. 
.
3. 
.
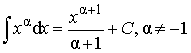4.
.
5. 
.
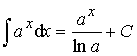6. 
.
7. 
.
8. 
.
9. 
.
10. 
.
11. 
.
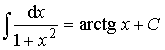12. 
.
13. 
.
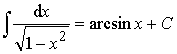14. 
.
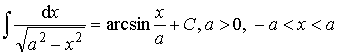15.
.
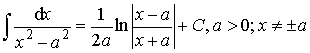16.
.
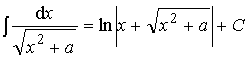В формулах 1-16 С
– произвольная постоянная.
Замечание.
Интеграл, взятый не от любой элементарной функции, является элементарной
функцией. Примерами могут служить следующие интегралы, часто встречающиеся в
задачах:
– интеграл Пуассона,
– интегралы Френеля,
– интегральный логарифм,
– интегральный косинус
и синус.
Указанные функции существуют и имеют
важное прикладное значение. Для этих функций составлены таблицы значений.