Тема 6. ИССЛЕДОВАНИЕ ФУНКЦИИ
6.1. Асимптоты графика функции
6.4. Выпуклость, вогнутость и точки
перегиба графика функции
6.5.
Наибольшее и наименьшее значения функции на отрезке
6.6. Схема исследования функции. Построение
графика
6.1. Асимптоты графика функции
Определение 1. Если точка M(x; y)
перемещается по кривой y =
f(x) так, что
хотя бы одна из координат точки стремится к ¥ и при этом расстояние от этой точки
до некоторой прямой стремится к 0, то эта прямая называется асимптотой кривой y = f(x).
Асимптоты бывают двух видов: вертикальные и наклонные.
Определение 2. Прямая x = a называется вертикальной асимптотой кривой
y =
f(x), если хотя
бы один из односторонних пределов ![]() или
или ![]() равен +¥ или
– ¥.
равен +¥ или
– ¥.
Замечание.
Если прямая x =
a является вертикальной асимптотой
кривой y = f(x), то в точке x = a функция f(x) имеет
разрыв второго рода. Наоборот, если в точке x = a функция f(x) имеет разрыв второго рода, то прямая x = a является
вертикальной асимптотой кривой y = f(x).
Определение 3. Прямая ![]() называется наклонной асимптотой кривой
называется наклонной асимптотой кривой ![]() при
при ![]() (или
(или ![]() ), если функцию f(x) можно
представить в виде:
), если функцию f(x) можно
представить в виде:
![]() ,
,
где ![]() (x) – бесконечно малая функция при
(x) – бесконечно малая функция при ![]() (или
(или ![]() ).
).
Теорема 1. Для того
чтобы кривая y =
f(x) имела
наклонную асимптоту при ![]() (или
(или![]() ) необходимо и достаточно существования двух конечных
пределов:
) необходимо и достаточно существования двух конечных
пределов:
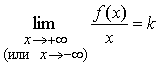 и
и 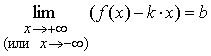
Доказательство. Ограничимся случаем ![]() .
.
Необходимость. Пусть y = kx+b – наклонная асимптота при ![]() кривой y = f(x). Тогда
функцию f(x) представим в виде:
кривой y = f(x). Тогда
функцию f(x) представим в виде:
![]() , где
, где ![]() при
при ![]() .
.
Убедимся в существовании конечных пределов:
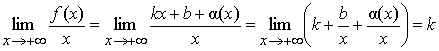 .
.
![]() .
.
Необходимость доказана.
Достаточность. Пусть существуют конечные пределы 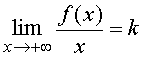 и
и ![]() .
.
Тогда по свойству конечных пределов
второй предел можно переписать в виде:
![]() ,
,
где ![]() (x) – бесконечно малая величина при
(x) – бесконечно малая величина при ![]() .
.
Отсюда получаем:
![]() ,
,
где ![]() при
при ![]() .
.
Достаточность доказана.
Пример 1.
Найти асимптоты кривой 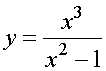 .
.
Решение.
1) D(y) = (–¥;–1) È (–1;1) È (1;+ ¥).
2) Точки x = –1 и x =
1 являются точками разрыва второго рода, так как:
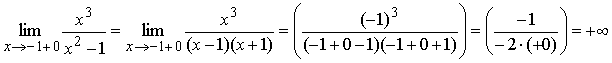
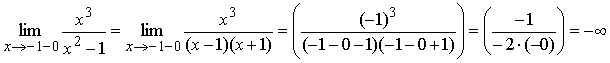
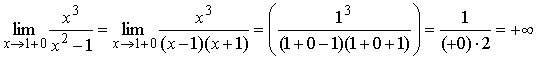
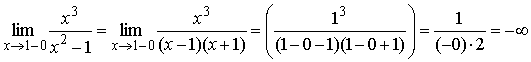
Поэтому прямые x = –1 и x = 1 являются вертикальными
асимптотами.
3) Вычислим пределы:
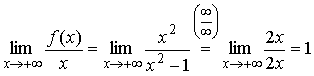 , k =
1.
, k =
1.
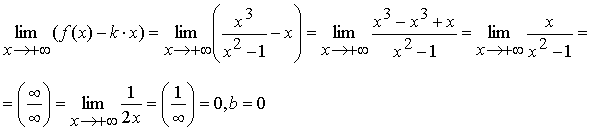
Отсюда следует, что при ![]() прямая y = 1×x +0, т.е. y = x –
наклонная асимптота при
прямая y = 1×x +0, т.е. y = x –
наклонная асимптота при ![]() .
.
Найдём наклонную асимптоту при ![]() .
.
Вычисляя те же пределы при ![]() , получим k = 1 и b = 0, т.е.
прямая y = x является наклонной асимптотой при
, получим k = 1 и b = 0, т.е.
прямая y = x является наклонной асимптотой при ![]() .
.
Ответ: x = ± 1 –
вертикальные асимптоты
y = x –
наклонная асимптота при x ® ±¥.
6.2. Монотонность функции
Определение 4. Функция y = f(x) называется
возрастающей (убывающей) на
промежутке (a;b), если для
любых x1 и x2, принадлежащих этому промежутку, из условия x2
> x1 следует неравенство:
f(x2) > f(x1)
(f(x2) < f(x1)).
Определение 5. Функция y = f(x) называется
монотонной на промежутке (a;b), если она на этом промежутке
является только возрастающей или только убывающей.
Теорема 2 (достаточные условия
монотонности). Если
функция y =
f(x)
дифференцируема на промежутке (a;b) и f’(x) > 0 (f’(x) < 0)
для любых x Î (a;b), то
функция возрастает (убывает) на этом промежутке.
Доказательство.
Возьмём любые два значения x1 и x2 из промежутка (a;b). Для определённости предположим, что x2 > x1.
На отрезке [x1;x2] функция y =
f(x) непрерывна
и дифференцируема (из условия теоремы). Следовательно, она удовлетворяет
теореме Лагранжа на отрезке [x1; x2], т.е. существует хотя бы одна точка c Î (x1; x2), в которой выполняется равенство:
f(x2) – f(x1) = f' (c) × (x2 – x1).
Если f '(x) > 0 для
любых xÎ(a;b), то f '(c) > 0. Поэтому f(x2) – f(x1) > 0, т.е. из условия x2 > x1 следует неравенство f(x2) > f(x1). А так как x1 и x2
–любые
значения из промежутка (a;b), то
функция y =
f(x) возрастает
на этом промежутке.
Если ![]() для любых
для любых ![]() , то
, то ![]() . Поэтому
. Поэтому![]() , то есть из условия x2 > x1 следует неравенство f(x2) < f(x1). Так как x1 и x2 любые значения из промежутка (a;b), то функция y = f(x) убывает на
этом промежутке.
, то есть из условия x2 > x1 следует неравенство f(x2) < f(x1). Так как x1 и x2 любые значения из промежутка (a;b), то функция y = f(x) убывает на
этом промежутке.
Теорема доказана.
6.3. Экстремумы функции
Определение 6. Функция y = f(x) имеет в
точке x0ÎD(f) максимум
ymax (минимум ymin), если существует такая окрестность
точки x0, в которой для всех x выполняется неравенство:
f(x0) > f(x) (f(x0) < f(x)).
Определение 7. Точки
максимума и минимума функции называются точками экстремума функции.
Теорема 3 (необходимое условие
экстремума). Если
функция y =
f(x) имеет
экстремум в точке x0, то в этой точке производная функции равна нулю или
не существует.
Доказательство. 1)Для определённости рассмотрим случай, когда функция y = f(x) в точке x0 имеет максимум и в этой точке существует производная.
Тогда из определения максимума для любого x,
принадлежащего окрестности точки x0
f(x0) > f(x).
Отсюда следует, что для любого Dx ≠ 0 справедливо
неравенство: f(x0+Dx) – f(x0) < 0. Разделим это неравенство на
Dx, получим:
при Dx > 0: 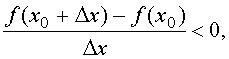
при Dx < 0: 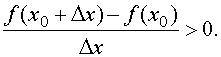
Перейдём к пределам:
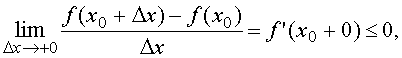
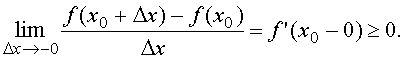
Так как![]() существует, то:
существует, то:
![]()
Аналогично рассматривается случай,
когда x0 – точка минимума.
2) Если f '(x0) не существует или равна ¥, то
точка x0 может быть точкой экстремума функции.
Например, функция y = ![]() имеет минимум при x = 0, хотя y'(0) не
существует (рис. 9).
имеет минимум при x = 0, хотя y'(0) не
существует (рис. 9).
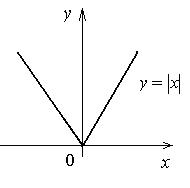
Рис. 9
Теорема доказана.
Теорема 4 (достаточное условие
экстремума). Если
функция y =
f(x) непрерывна
в точке x0, дифференцируема в некоторой её окрестности, за
исключением может быть самой этой точки, f’(x0) = 0 или не существует и при переходе x через точку x0 производная f '(x) изменяет знак, то точка x0 является точкой экстремума. Если при этом знак
f '(x) меняется
с
+ на –, то x0 – точка максимума,
с
– на +, то x0 – точка минимума.
Доказательство.
Пусть f '(x) при переходе x через точку
x0 изменяет знак с
+
на – , т.е. f '(x) > 0 при x Î
(x0 – d; x0) и
f '(x) <
0 при x Î (x0; x0 + d),
где d > 0
(рис. 10).
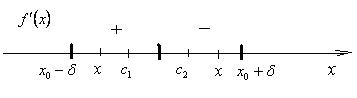
1) Пусть x Î (x0 – d; x0). На отрезке [x; x0] функция y =
f(x)
удовлетворяет теореме Лагранжа. Значит, на интервале (x; x0) найдётся хотя бы одна точка c1, в которой выполняется равенство:
f(x) – f(x0) = f '(c1)×(x –
x0),
где c1Î (x0 – d; x0).
Так как f '(c1) > 0 и x – x0 < 0,
то f(x) – f(x0) < 0.
2) Пусть ![]() . На отрезке
. На отрезке ![]() функция
функция ![]() также удовлетворяет
теореме Лагранжа. Значит на интервале (x0; x) найдётся
хотя бы одна точка с2, в
которой выполняется равенство:
также удовлетворяет
теореме Лагранжа. Значит на интервале (x0; x) найдётся
хотя бы одна точка с2, в
которой выполняется равенство:
f(x) – f(x0) = f’(c2)×(x – x0),
где c2 Î (x0; x0 + d).
Так как f '(c2) <
0 и x – x0 > 0, то f(x) – f(x0) < 0.
Следовательно, для любого x Î (x0 – d; x0 + d) выполняется неравенство: f(x0) > f(x).
Отсюда
следует, что точка x0 является точкой
максимума функции y = f(x). Аналогично рассматривается случай, когда ![]() при переходе x через точку x0 изменяет знак с – на +. При этом
точка x0 является точкой минимума функции
при переходе x через точку x0 изменяет знак с – на +. При этом
точка x0 является точкой минимума функции ![]() .
.
Теорема
доказана.
6.4. Выпуклость, вогнутость и точки перегиба графика функции
Пусть функция y = f(x)
дифференцируема в любой точке промежутка (a;b). Тогда она имеет конечную производную в любой точке
этого промежутка. Значит, существует касательная к графику функции y = f(x) в любой
его точке (x; f(x)) при a < x < b.
Определение 8. График функции y = f(x),
дифференцируемой в каждой точке промежутка (a;b), называется выпуклым
(вогнутым) на этом промежутке, если для любого x Î (a;b) график
расположен не выше (не ниже) касательной к графику в точке (x; f(x)).
Теорема 5 (достаточное условие
выпуклости или вогнутости кривой).
Пусть функция y = f(x) дважды дифференцируема
на промежутке (a;b) и f ''(x) для x Î (a;b) сохраняет свой знак, тогда кривая y = f(x) выпуклая, если f ''(x) £ 0
при x Î (a;b), и кривая y = f(x) вогнутая, если f ''(x) ³ 0 при x Î (a;b).
Доказательство.
Для определённости рассмотрим случай, когда f ''(x) ³ 0 для x Î (a;b). Обозначим x0 любую точку промежутка (a;b). Построим касательную к кривой y = f(x) в точке (x0; f(x0)): yкасат = f(x0) + f '(x0)∙(x – x0). Покажем, что график функции y = f(x) лежит не
ниже этой касательной,
т.е. выполняется неравенство: (f(x) – yкасат(x)) ³ 0 для любого x Î (a;b) (рис.11).
f(x) – yкасат(x) = f(x) – (f(x0) + f '(x0)∙(x – x0)) =
= f(x)
– f(x0) – f '(x0)∙(x – x0)
= (f(x) – f(x0)) – f '(x0)∙(x – x0), (1)
где x Î (a;b) .
Функция y = f(x) на отрезке [x0;x] удовлетворяет условию теоремы
Лагранжа, т.е. на отрезке [x0;x] найдётся хотя бы одна точка c1, для которой
выполняется равенство:
f (x) –
f(x0) =
f '(c1)∙(x – x0).
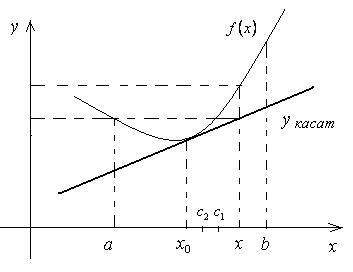
Подставим
в равенство (1) полученное соотношение.
f(x) – yкасат(x) = f '(c1)(x– x0) – f ' (x0)(x – x0) =
(x – x0)×(f ' (c1) – f ' (x0)). (2)
Функция
f '(x) на отрезке
[x0;c1]
удовлетворяет условию теоремы Лагранжа, т.е. на промежутке (x0;c1) найдётся хотя бы одна точка с2, для которой выполняется равенство:
f '(c1) – f '(x0) = f ''(c2)(c1 – x0).
Подставим в равенство (2) полученное
соотношение:
f(x) – yкасат(x) = (x – x0)×f ''(c2)∙(c1 – x0). (3)
Если x > x0, то c1 > x0 и c2 > x0,
т.е. x – x0 > 0 и с1 – x0 > 0.
По
предположению f ''(x) ³ 0. Тогда f(x) – yкасат(x) ³ 0.
Если x < x0, то c1 < x0 и
c2 < x0, т.е. x – x0 < 0 и c1 – x0 < 0. Тогда f(x) – yкасат(x) ³ 0.
Следовательно, при любом x Î (a;b) выполняется неравенство:
f(x) – yкасат(x) ³ 0,
т.е. на промежутке (a,b) график функции y = f(x) вогнутый.
Аналогично можно доказать, что если f ''(x) £ 0 при любом x Î (a;b), то кривая y = f(x) на промежутке (a;b) будет выпуклой.
Теорема доказана.
Определение 9. Пусть в
точке (x0; f(x0)) существует касательная. Тогда
точка (x0; f(x0)), отделяющая выпуклую часть кривой
от вогнутой (или наоборот) называется точкой
перегиба графика функции y = f(x).
Теорема 6 (достаточное условие точки
перегиба). Если функция
y = f(x) дважды дифференцируема в окрестности точки x0, вторая производная функции f ''(x0) = 0 (или не существует) и f ''(x) меняет свой знак при переходе x через точку x0, то точка (x0; f(x0)) – точка перегиба кривой y = f(x).
Доказательство.
Для определенности рассмотрим случай, когда f ''(x) при переходе через точку x0 изменяет знак с + на –.
Тогда в левой полуокрестности точки x0
f ''(x) > 0, т.
е. кривая при x < x0 вогнутая, а в правой полуокрестности точки x0 f ''(x) < 0, т.
е. кривая при x > x0 выпуклая.
Следовательно, точка (x0; f(x0)) по определению является точкой
перегиба графика функции y = f(x).
Аналогично рассматривается другой
случай, когда f ''(x) при
переходе
через точку x0 изменяет знак с
– на +.
Теорема доказана.
6.5. Наибольшее и наименьшее значения функции на отрезке
Пусть функция y = f(x) определена
на отрезке [a;b].
Определение 10. Число f(c) называется
наибольшим (наименьшим) значением функции y = f(x) на отрезке [a;b] и обозначается ![]() (
(![]() ), если для любого x Î
[a;b]
выполняется неравенство:
), если для любого x Î
[a;b]
выполняется неравенство:
f(x) £ f(c)
(f(x) ³ f(c)) .
Если функция y = f(x) непрерывна
на отрезке [a;b], то по
свойству непрерывной на отрезке функции она
достигает своих наибольшего
и наименьшего значений.
Схема нахождения этих значений
следующая:
1) Найти все точки, в которых f '(x) = 0 (или не существует). Причём выбрать те точки из
полученных, которые попадают на отрезок [a;b].
2) Вычислить значения функции в
полученных точках в п.1.
3) Вычислить значения функции в
граничных точках отрезка [a;b]: f(a) и f(b).
4) Из значений п.2 и п.3 найти
наибольшее число M и наименьшее m.
Тогда ![]()
![]()
6.6. Схема исследования функции. Построение графика
1) Найти область определения функции y = f(x) – множество D(f) тех значений x, при которых функция y = f(x) имеет смысл.
2) Исследовать функцию на периодичность: выяснить, существует ли
наименьшее положительное число T такое, что f(x+T) = f(x) для любого
xÎ D(f). Если «да», то целесообразно далее
исследовать функцию и строить её график только на некотором отрезке длиной
периода T. Затем продолжить график на всю
область определения, разбивая её на интервалы длины T, в которых
повторяется картинка графика.
3)
Исследовать функцию на чётность и нечётность: выяснить, выполняются ли равенства:
f(– x) = f(x) для любого xÎ D(f) – чётность
или
f(– x) = – f(x) для любого xÎ D(f) – нечётность.
Это позволяет узнать, есть ли
симметрия графика: относительно оси Oy –
чётная или относительно начала координат – нечётная.
4) Найти точки пересечения графика
функции![]() с осями координат:
с осями координат:
· с осью Oy: точка (0; f(0)), если 0 Î D(f),
· с осью Oх: точка (xk; 0), где xkÎ D(f) и является решением уравнения f(x) = 0.
5) Найти промежутки знакопостоянства: выяснить, при каких x Î D(f) выполняются неравенства f(x) > 0 (график функции расположен
выше оси Ox) и f(x) < 0 (график функции расположен ниже оси Ox).
6) Исследовать функцию на непрерывность, установить тип точек разрыва.
7) Найти вертикальные и
наклонные асимптоты..
8) Найти промежутки убывания и возрастания, экстремумы функции.
9) Найти множество E(f) значений функции.
10) Найти промежутки выпуклости, вогнутости и точки перегиба графика.
11) Построить график функции, используя свойства, установленные в
проведенном исследовании. Если в некоторых промежутках график остался неясным,
то его уточняют по дополнительным точкам.
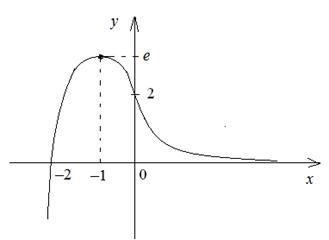
Пример.
Исследовать функцию y = (x + 2)e–x и построить её
график.
1) D(y) = R.
2) Функция не периодическая.
3) Так как y(–x) ≠ y(x) и y(–x) ≠ –y(x), то функция общего вида, не
является ни чётной, ни нечётной.
4) Точка пересечения графика с осью Ox : (– 2; 0), с Oy : (0; 2)
5) При x Î (–¥; –2) функция отрицательная, при x Î (–2; +¥) функция положительная.
6) Функция непрерывна при x Î R.
7) Вертикальных асимптот нет.
Наклонные асимптоты: y = kx + b.
а) 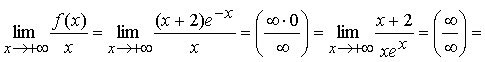
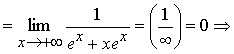 k = 0 при x ® +¥
k = 0 при x ® +¥
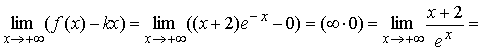
![]()
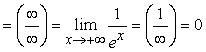
b = 0 при ![]() .
.
Следовательно, y = 0 – наклонная (горизонтальная) асимптота при ![]() .
.
б) ![]()
при ![]() наклонной асимптоты
нет.
наклонной асимптоты
нет.
8) f
'(x) = ((x + 2)e– x) ' = 1×e– x+(x + 2)×(–e–x) = e–x(1 – x – 2) = –(x + 1)e– x.
D(y') = R.
y ' = 0: – (x+1)e– x = 0 Þ x = – 1, f(–1)
= 1×e1 = e.
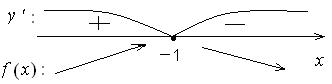
при x Î (– ¥;– 1) f(x)
возрастает,
при x Î(– 1;+¥) f(x) убывает,
при x = –1 fmax
(– 1) = (– 1+2)e– (– 1)
= e.
9) E(f) = (–¥; e), так как
![]()
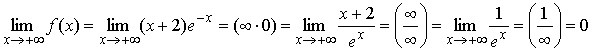
и fmax (–1) = e.
10) f ''(x) = (– (x + 1)e– x) ' = – 1e– x + (x + 1)e–x = e– x(x + 1 – 1) = xe–x.
D(f '') = R
f '' (x) = 0 : xe– x = 0 Þ x = 0,
f(0) = 2.

при x Î (– ¥;0) график f(x) выпуклый
при x Î (0;+¥) график f(x) вогнутый
Точка (0;2) – точка перегиба графика.
11) Результаты проведенного исследования cведём в таблицу и построим график
(рис. 12)
Таблица
Результаты исследования функции y = (x + 2)e – x
|
x |
(– ¥;–
1) |
–
1 |
(– 1;0) |
0 |
(0;+¥) |
|
знак f
' (x) |
+ |
0 |
– |
– |
– |
|
знак f '' (x) |
– |
– |
– |
0 |
+ |
|
F(x) |
|
e |
|
2 |
|
|
|
|
|
|
|