Тема 1. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ

1.1. Определение функции одной переменной

Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f(x) с областью определения X = D(f) и областью изменения Y = E(f). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.

Частным значением функции y = f(x) при фиксированном значении аргумента x = x₀ называют y₀= f(x₀).

Графиком функции y = f(x) называют геометрическое место точек M(x;f(x)) на плоскости Oxy, где x Î D(f) и f(x) Î E(f).

1.2. Способы задания функции

1) Аналитический способ – способ задания функции с помощью формулы.

Различают несколько способов аналитического задания функции:

а) Функция задана явно формулой y = f(x).

Например: 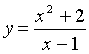, где D(y) = (– ∞;1)(1;+∞).

б) Функция задана неявно уравнением, связывающем x и y: F(x;y) = 0.

Например: – уравнение окружности с центром в начале координат и радиусом r. Если из этого уравнения выразить y через x, то получится две функции:

и ,

которые имеют область определения , а области значений этих функций будут: для первой – , для второй – .

в) Функция задана параметрически с помощью некоторого параметра t, причём и аргумент x, и функция y зависят от этого параметра:

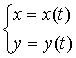
Например: можно задать окружность с помощью параметрических уравнений:

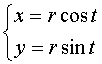
2) Табличный способ задания функции – например, таблицы Брадиса задают функции y = sin x, y = cos x и др.

3) Графический способ задания функции, когда зависимость функции от её аргумента задаётся графически.

1.3. Сложная и обратная функции

Определение 1. Пусть функция y = f(U) определена на множестве D(f), а функция U = g(x) определена на D(g), причём E(g)D(f).

Тогда функция y = F(x) = f(g(x)) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g ).

Определение 2. Пусть задана функция y = f(x) взаимно однозначно отображающая множество X = D(f) на множество Y = E(f). Тогда функция x = g(y) называется обратной к функции y = f(x), т. е. любому yE(f) соответствует единственное значение xD(f), при котором верно равенство y = f(x).

Замечание. Графики функций y = f(x) и x = g(y) представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить x, а зависимую y, то графики функций y = f(x) и y = g(x) будут симметричны относительно биссектрисы первого и третьего координатных углов.

1.4. Элементарные функции

Основные элементарные функции:

y = const (постоянная функция), D(y) = R; E(y) = c.

(линейная функция), D(y) = R; E(y) = R.

y =(степенная функция), α ÎR, E(y), D(y) зависят от α.

y = (показательная функция), a > 0, a ≠ 1, D(y) = R, E(y) = (0;+∞).

y =(логарифмическая функция) ), a > 0, a ≠ 1, D(y) = (0;+∞), E(y) = R.

Тригонометрические функции:

y = sin x, D(y) = R, E(y) =.

y = cos x, D(y) = R, E(y) =.

y = tg x, D(y) = , E(y) = R.

y = ctg x, D(y) = , E(y) = R.

Обратные тригонометрические функции:

y = arcsin x, D(y) = , E(y) = .

y = arccos x, D(y) = , E(y) = .

y = arctg x, D(y) = R, E(y) = .

y = arcctg x, D(y) = R, E(y) = .

Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции.

Например: – элементарная функция.

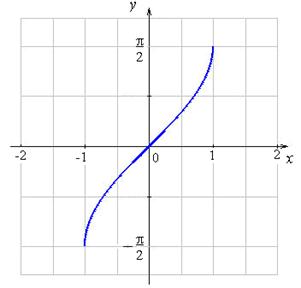
Графики обратных тригонометрических функций:

y = arcsin x

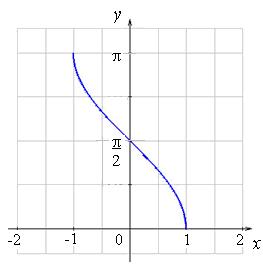
y = arccos x

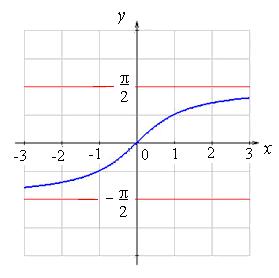
y = arctg x

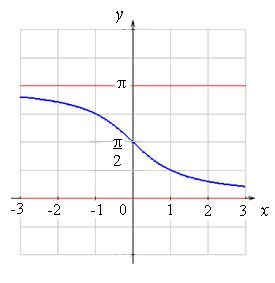
y = arcctg x