Тема 7. Производные и дифференциалы высших порядков. Формула Тейлора

7.1. Производные высших порядков

Пусть функция , определённая на интервале , имеет в каждой точке производную и пусть . Если при x = x₀ у производной функции существует производная, то она называется второй производной (или производной второго порядка) функции f и обозначается или .

Таким образом, . Аналогично определяется производная любого порядка n=1, 2, ...: если существует производная порядка n–1 (при этом под производной нулевого порядка подразумевается сама функция , а под производной первого порядка – ), то, по определению, .

Вспоминая определение производной, определение n-й производной в точке x₀ можно записать в виде предела:

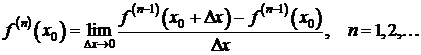
Отметим, из предположения, что функция f имеет в точке x₀ производную порядка n, отсюда следует, в силу определения последней, что в некоторой
окрестности точки x₀ у функции f существует производная порядка n–1, а, следовательно, при n > 1 и все производные более низкого порядка k < n–1, в частности, сама функция определена в некоторой окрестности точки x₀. При этом все производные, порядок которых меньше n–1, непрерывны в указанной окрестности, поскольку во всех её точках они имеют производную.

Функция называется n раз непрерывно дифференцируемой на некотором промежутке, если во всех точках этого промежутка она имеет непрерывные производные до порядка n включительно (n = 1, 2, ...).

Для того чтобы функция была n раз непрерывно дифференцируемой на некотором промежутке, достаточно, чтобы она имела на нём непрерывную производную порядка n.

Теорема. Пусть функции и имеют производные n-го порядка в точке x₀; тогда функции и имеют производные n-го порядка в точке x₀, причём , 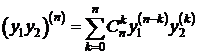. (1)

Здесь, как обычно, – число сочетаний из n элементов по k.

Формулу (1) обычно называют формулой Лейбница.

7.2. Формула Тейлора

Теорема. Пусть функция , определённая на интервале , имеет в точке производные до порядка n включительно. Тогда при x®x₀

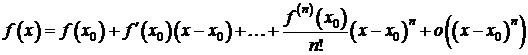
или .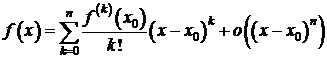

Эта формула называется формулой Тейлора n-го порядка с остаточным членом в форме Пеано.

Многочлен

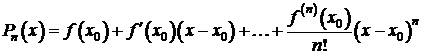называется многочленом Тейлора степени n, а функция – остаточным членом n-го порядка формулы Тейлора.

Если в формуле Тейлора положить x₀= 0, то получается частный вид формулы Тейлора, называемый обычно формулой Маклорена:

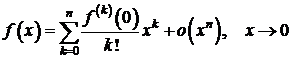Теорема позволяет любую функцию, удовлетворяющую условиям этой теоремы, заменить в окрестности некоторой точки многочленом с точностью до бесконечно малых более высокого порядка, чем члены многочлена. Таким многочленом является многочлен Тейлора. Величина погрешности определяется при этом остаточным членом.

Замечание. Можно показать, что если функция в некоторой окрестности точки x₀ имеет производную порядка n, то, какова бы ни была точка x этой окрестности, найдётся такая точка x, лежащая между x₀ и x, что для остаточного члена формулы Тейлора функции имеет место формула

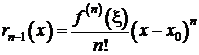(форма Лагранжа), 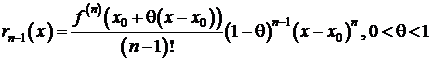(форма Коши).